Logic Programming with MaxClique and its Application to

Logic Programming with Max-Clique and its Application to Graph Coloring MORAD MUSLIMANY Ben-Gurion University of the Negev Joint work with: Michael Codish, Michael Frank, Amit Metodi {mcodish, frankm, moradm, amitmet}@cs. bgu. ac. il

Logic Programming with Max-Clique and its Application to Graph Coloring We will present pl-cliquer, a Prolog interface to the cliquer tool for the maximum clique problem. Agenda: • Problem definitions and examples • pl-cliquer • Usage examples • Experiments

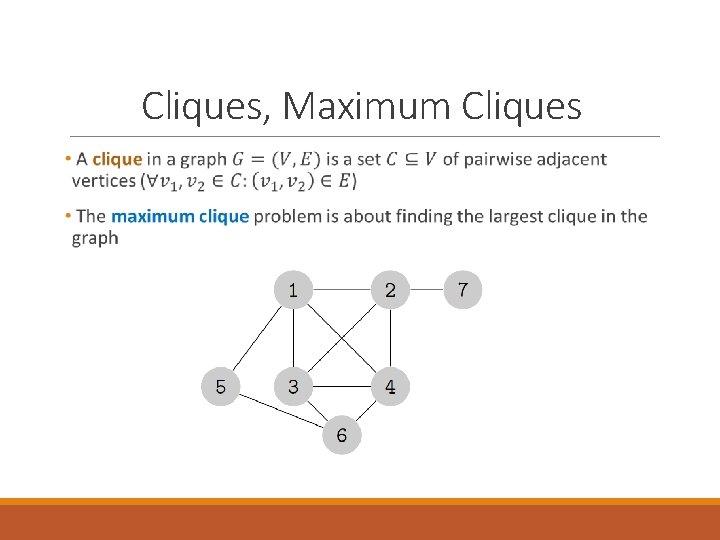
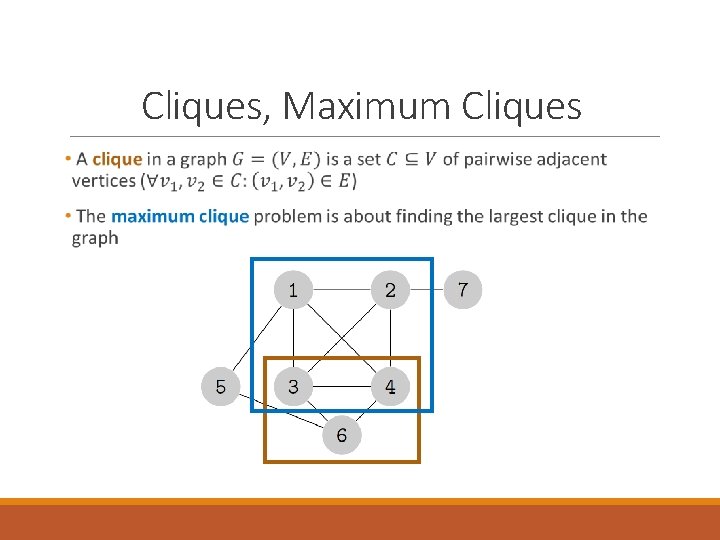
Cliques, Maximum Cliques

Cliques, Maximum Cliques

Graph Coloring

Graph Coloring

Cliques and colorings

Hardness of these problems

Hard but solvable in practice… • Although the problem of maximum-clique is NP-Hard, it is solvable in practice in many graphs by various tools • Cliquer is one such tool, which is a set of C routines for finding cliques in a graph

Logic Programming with Max-Clique and its Application to Graph Coloring We will present pl-cliquer, a Prolog interface to the Cliquer tool for the maximum clique problem. Agenda: • Problem definitions and examples • pl-cliquer • Usage examples • Experiments

pl-cliquer • We have written an interface that connects Cliquer with SWI-Prolog, called pl-cliquer • Provides five high-level predicates, and we will focus on the following three: 1. graph_read_dimacs_file/5 2. clique_find_single/4 3. clique_find_n_sols/6

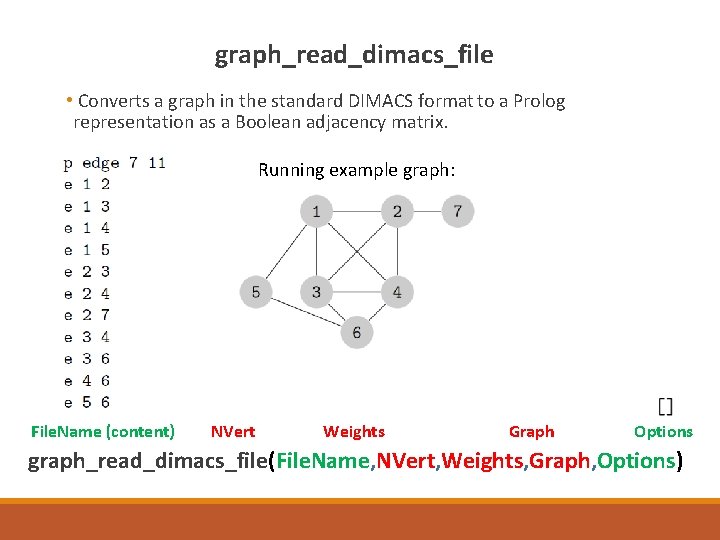
graph_read_dimacs_file • Converts a graph in the standard DIMACS format to a Prolog representation as a Boolean adjacency matrix. Running example graph: File. Name (content) NVert Weights Graph Options graph_read_dimacs_file(File. Name, NVert, Weights, Graph, Options)

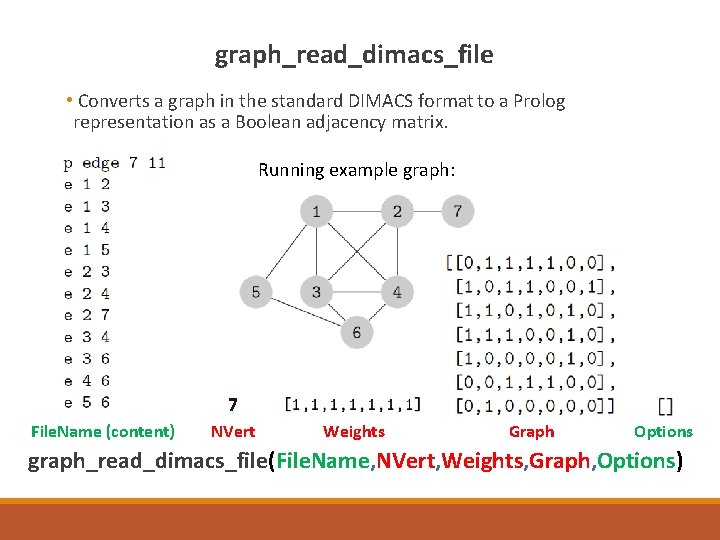
graph_read_dimacs_file • Converts a graph in the standard DIMACS format to a Prolog representation as a Boolean adjacency matrix. Running example graph: 7 File. Name (content) NVert Weights Graph Options graph_read_dimacs_file(File. Name, NVert, Weights, Graph, Options)

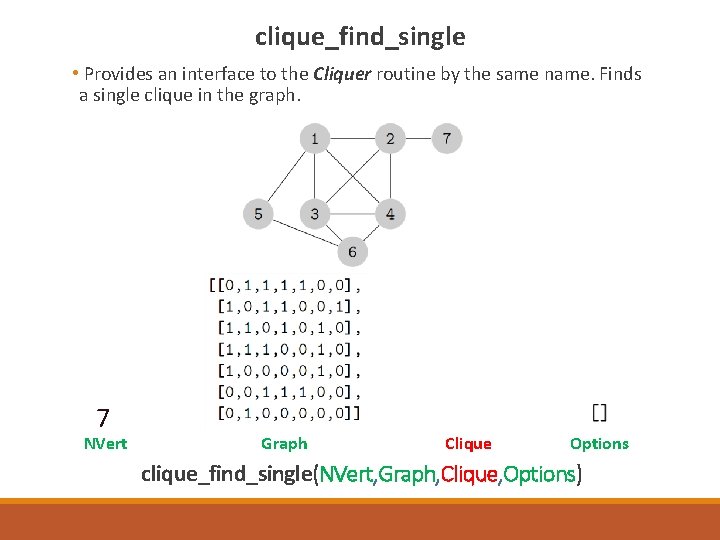
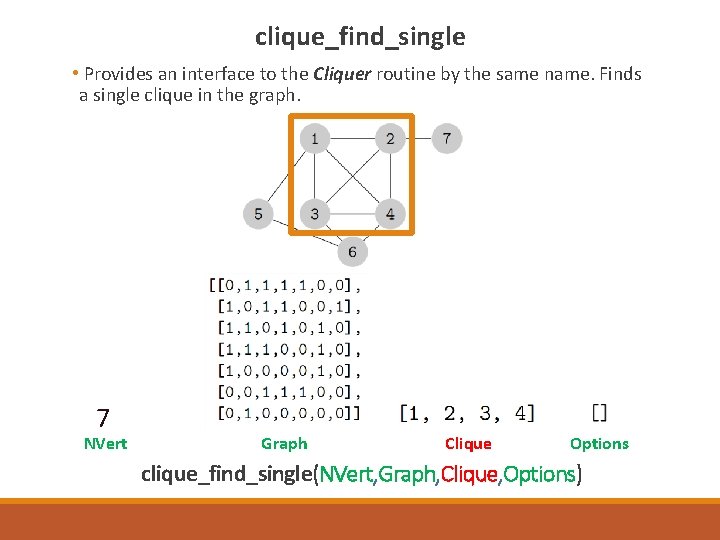
clique_find_single • Provides an interface to the Cliquer routine by the same name. Finds a single clique in the graph. 7 NVert Graph Clique Options clique_find_single(NVert, Graph, Clique, Options)

clique_find_single • Provides an interface to the Cliquer routine by the same name. Finds a single clique in the graph. 7 NVert Graph Clique Options clique_find_single(NVert, Graph, Clique, Options)

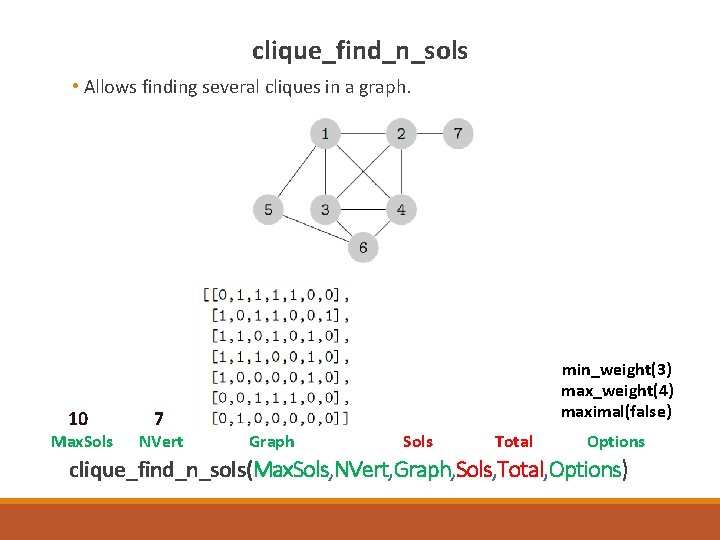
clique_find_n_sols • Allows finding several cliques in a graph. 10 Max. Sols 7 NVert min_weight(3) max_weight(4) maximal(false) Graph Sols Total Options clique_find_n_sols(Max. Sols, NVert, Graph, Sols, Total, Options)

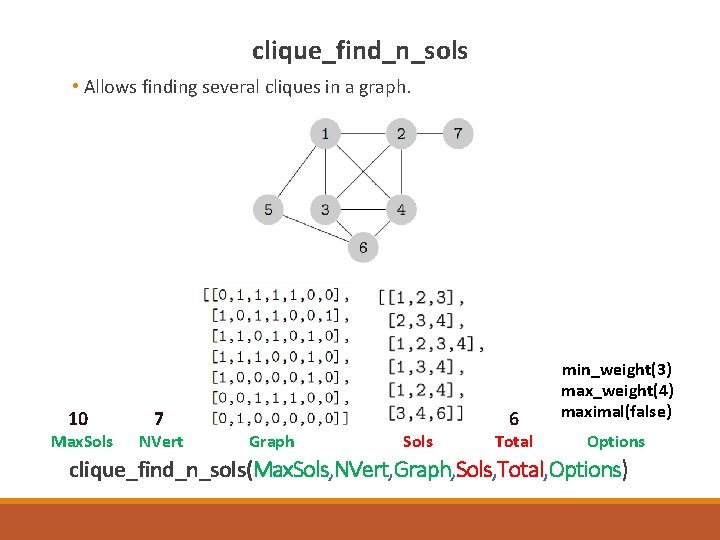
clique_find_n_sols • Allows finding several cliques in a graph. 10 Max. Sols 7 NVert Graph Sols 6 Total min_weight(3) max_weight(4) maximal(false) Options clique_find_n_sols(Max. Sols, NVert, Graph, Sols, Total, Options)

Logic Programming with Max-Clique and its Application to Graph Coloring We will present pl-cliquer, a Prolog interface to the cliquer tool for the maximum clique problem. Agenda: • Problem definitions and examples • pl-cliquer • Usage examples • Experiments

Solving the Graph Coloring Problem 1. We model the problem using a constraint language (BEE) 2. The constraints model is then compiled to SAT using the BEE compiler (written in Prolog) 3. The SAT instance is solved using a SAT solver via the Prolog interface (BEE allows a variety of solvers at its backend) 4. The satisfied SAT instance assignment is decoded back to a graph coloring

Main Predicate 1. We model the problem using a constraint language (BEE) 2. The constraints model is then compiled to SAT using the BEE compiler (written in Prolog) 3. The SAT instance is solved using a SAT solver via the Prolog interface (BEE allows a variety of solvers at its backend) 4. The satisfied SAT instance assignment is decoded back to a graph coloring

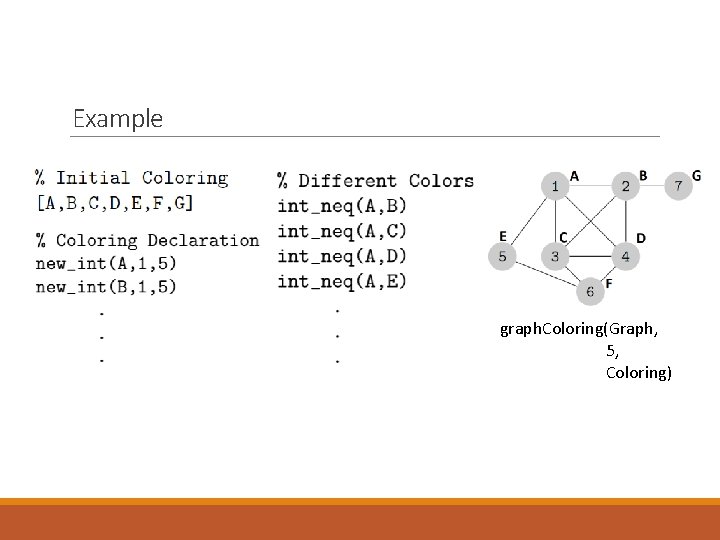
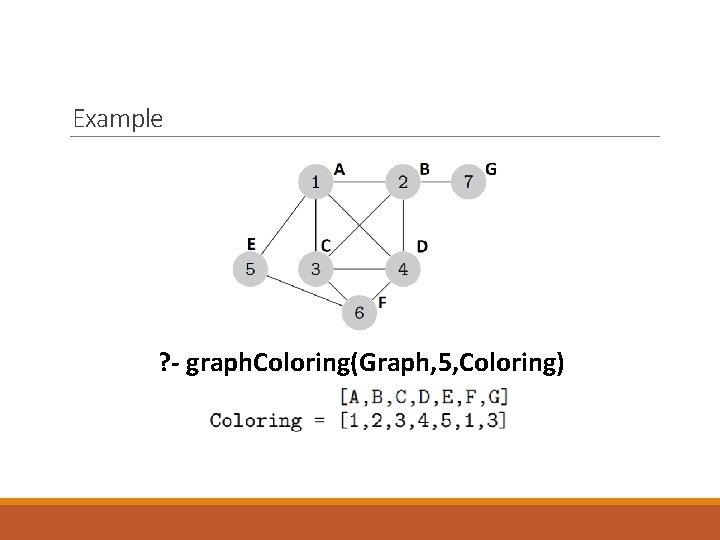
Example Can we solve our running example with 5 colors? ? - graph. Coloring(Graph, 5, Coloring)

Example graph. Coloring(Graph, 5, Coloring)

Example ? - graph. Coloring(Graph, 5, Coloring)

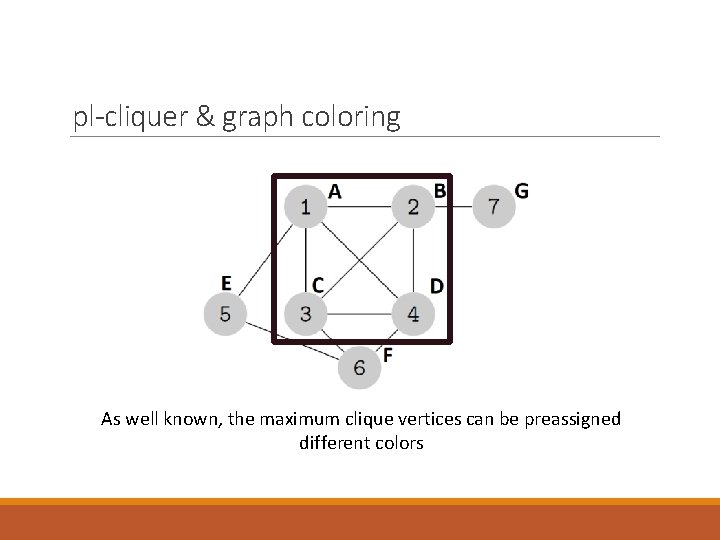
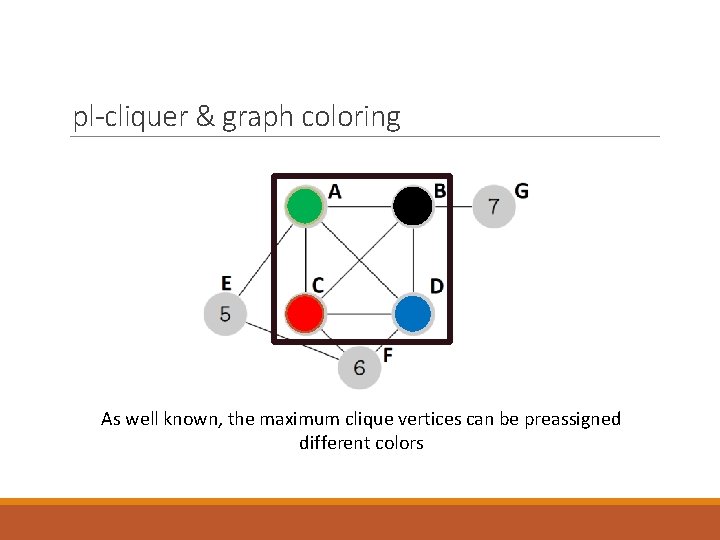
pl-cliquer & graph coloring As well known, the maximum clique vertices can be preassigned different colors

pl-cliquer & graph coloring As well known, the maximum clique vertices can be preassigned different colors

pl-cliquer & graph coloring

Example – with pl-cliquer graph. Coloring(Graph, 5, Coloring)

Logic Programming with Max-Clique and its Application to Graph Coloring We will present pl-cliquer, a Prolog interface to the cliquer tool for the maximum clique problem. Agenda: • Problem definitions and examples • pl-cliquer • Usage examples • Experiments

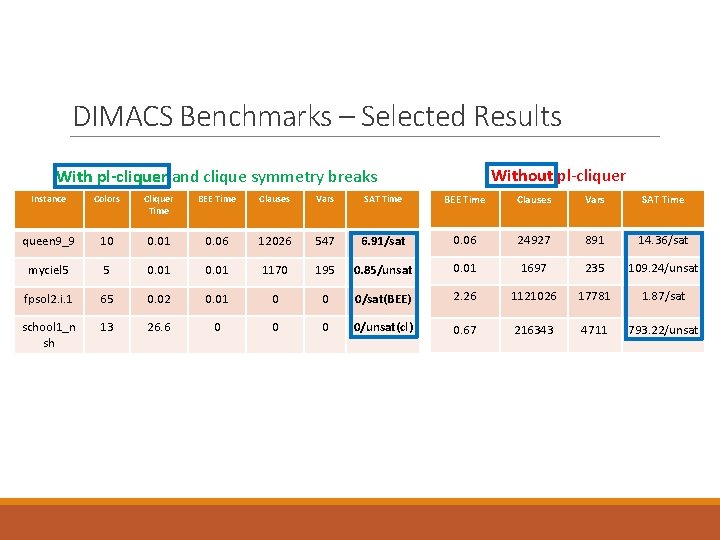
DIMACS Benchmarks – Selected Results Without pl-cliquer With pl-cliquer and clique symmetry breaks Instance Colors Cliquer Time BEE Time Clauses Vars SAT Time queen 9_9 10 0. 01 0. 06 12026 547 6. 91/sat 0. 06 24927 891 14. 36/sat myciel 5 5 0. 01 1170 195 0. 85/unsat 0. 01 1697 235 109. 24/unsat fpsol 2. i. 1 65 0. 02 0. 01 0 0 0/sat(BEE) 2. 26 1121026 17781 1. 87/sat school 1_n sh 13 26. 6 0 0/unsat(cl) 0. 67 216343 4711 793. 22/unsat

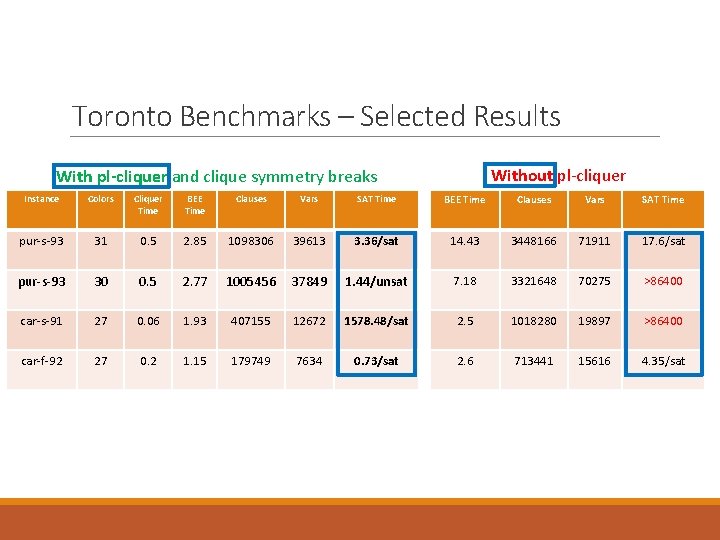
Toronto Benchmarks – Selected Results Without pl-cliquer With pl-cliquer and clique symmetry breaks Instance Colors Cliquer Time BEE Time Clauses Vars SAT Time pur-s-93 31 0. 5 2. 85 1098306 39613 3. 36/sat 14. 43 3448166 71911 17. 6/sat pur-s-93 30 0. 5 2. 77 1005456 37849 1. 44/unsat 7. 18 3321648 70275 >86400 car-s-91 27 0. 06 1. 93 407155 12672 1578. 48/sat 2. 5 1018280 19897 >86400 car-f-92 27 0. 2 1. 15 179749 7634 0. 73/sat 2. 6 713441 15616 4. 35/sat

Questions?