Mechanisms of chaos in the forced NLS equation

Mechanisms of chaos in the forced NLS equation Eli Shlizerman Vered Rom-Kedar Weizmann Institute of Science eli. shlizerman@weizmann. ac. il http: //www. wisdom. weizmann. ac. il/~elis/

The autonomous NLS equation • Boundary • Periodic • Even B(x+L, t) = B(x, t) B(-x, t) = B(x, t) • Parameters • Wavenumber k = 2π / L • Forcing Frequency Ω 2

Integrals of motion • The “Particle Number”: • The “Energy”: • The “Perturbation”:

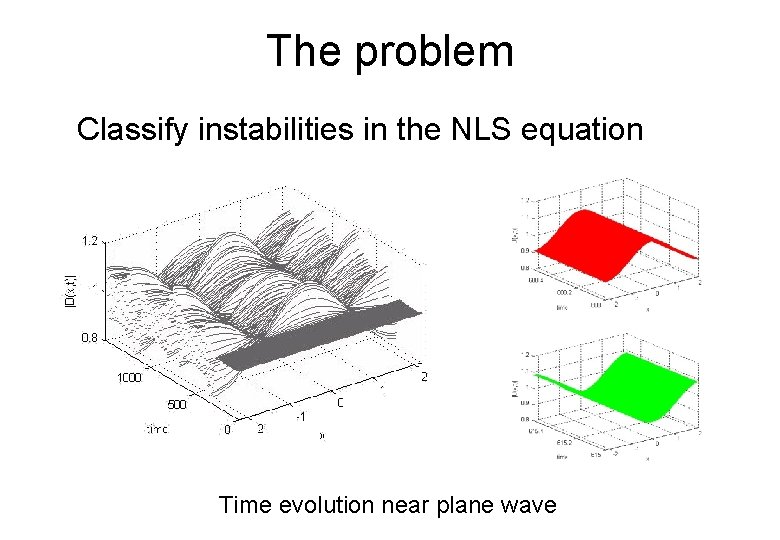
The problem Classify instabilities in the NLS equation Time evolution near plane wave

Solitons • Solitary wave • Permanent shape B (x , t) = g (x) • Traveling wave solution B (x , t) = g (x - vt) • Localized g (r) = 0 r →±∞ • Particle like • Preserved under collisions

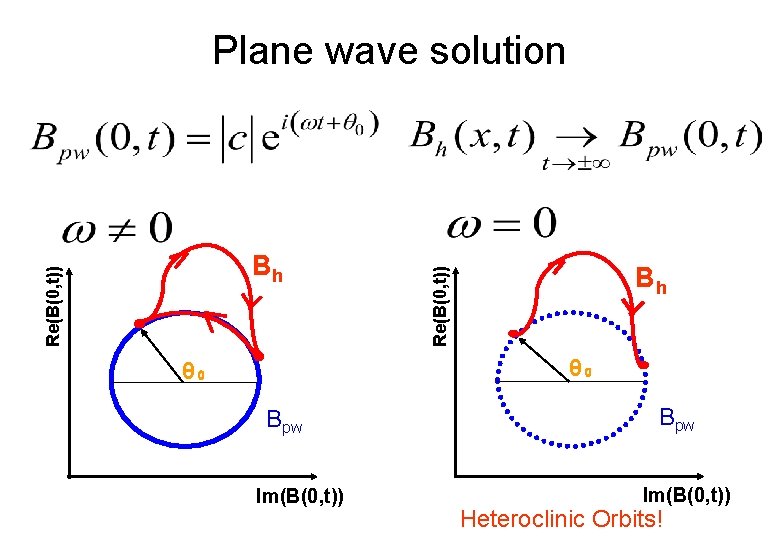
Plane wave solution Bh Re(B(0, t)) Bh θ₀ θ₀ Bpw Im(B(0, t)) Heteroclinic Orbits!

Modal equations • Consider two mode Fourier truncation B(x , t) = c (t) + b (t) cos (kx) • Substitute into the unperturbed eq. : [Bishop, Mc. Laughlin, Ercolani, Forest, Overmann]

General Action-Angle Coordinates • For b≠ 0 , consider the transformation: • Then the systems is transformed to: • We can study the structure of [Kovacic]

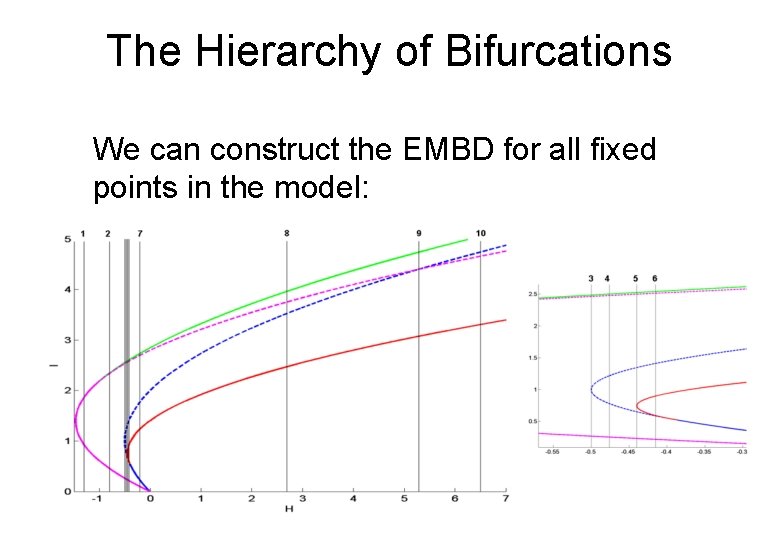
The Hierarchy of Bifurcations Local Stability for I < 2 k 2 Fixed Point x=0 y=0 x=±x 2 y=0 Stable I>0 I > ½k 2 Unstable I > ½ k 2 - Fixed points in (x, y) are circles in 4 dimensional space

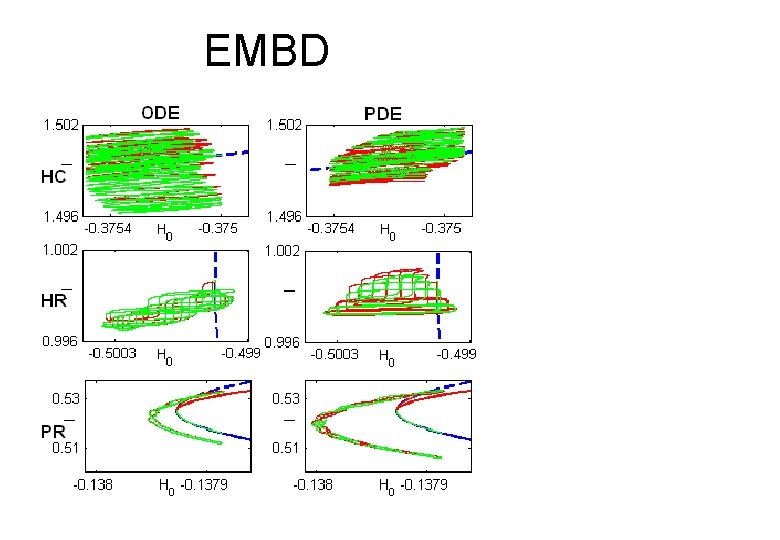
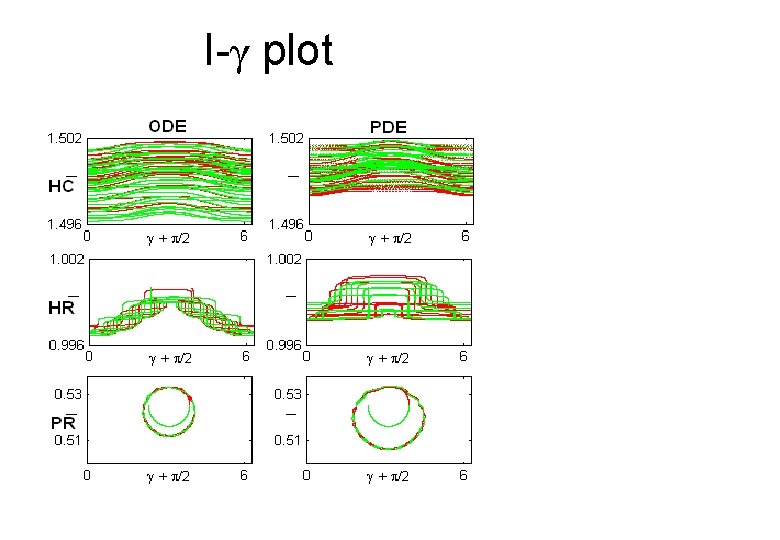
Perturbed motion classification near the plane wave • “Standard” dyn. phenomena • Homoclinic Chaos, Elliptic Circles • Special dyn. phenomena • PR, ER, HR I • Close to the integrable motion H 0 Dashed – Unstable Solid – Stable

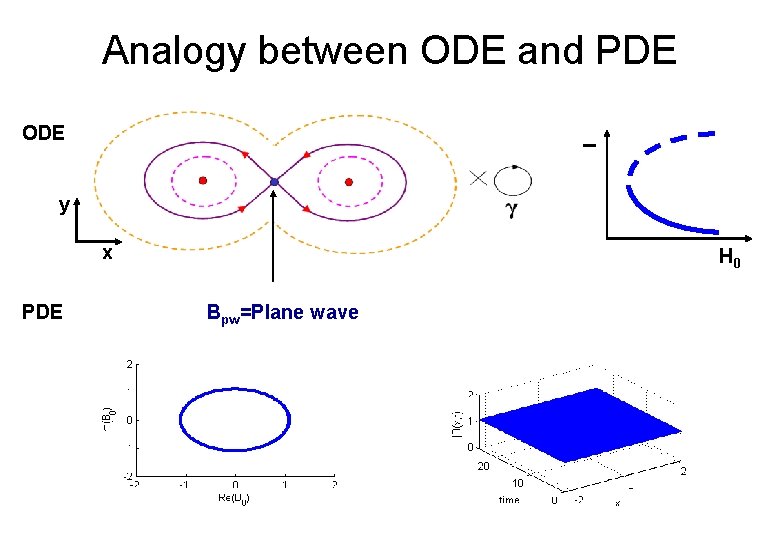
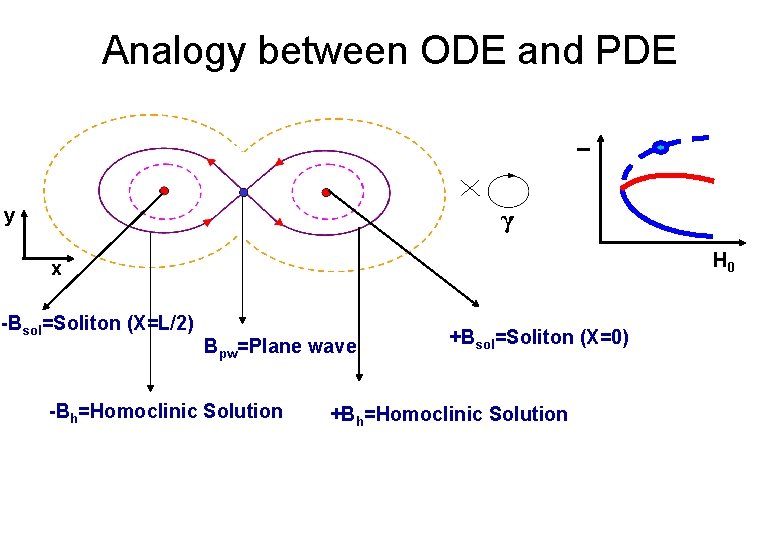
Analogy between ODE and PDE I ODE y x PDE H 0 Bpw=Plane wave

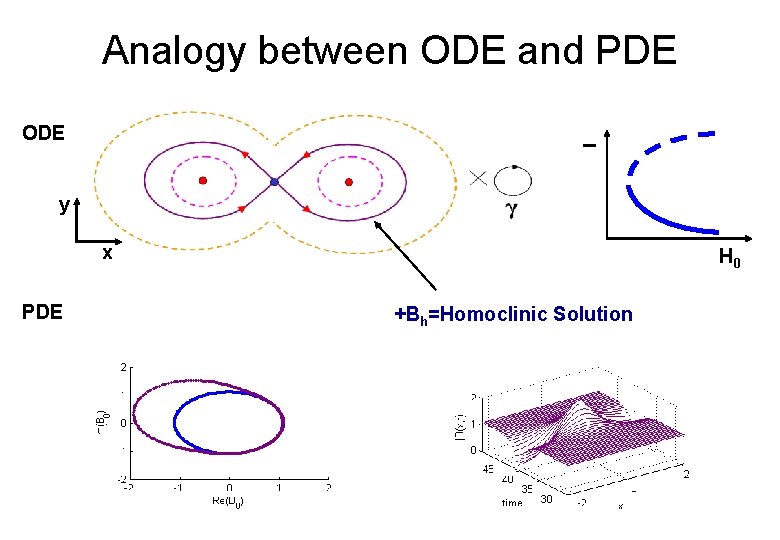
Analogy between ODE and PDE I ODE y x PDE H 0 +Bh=Homoclinic Solution

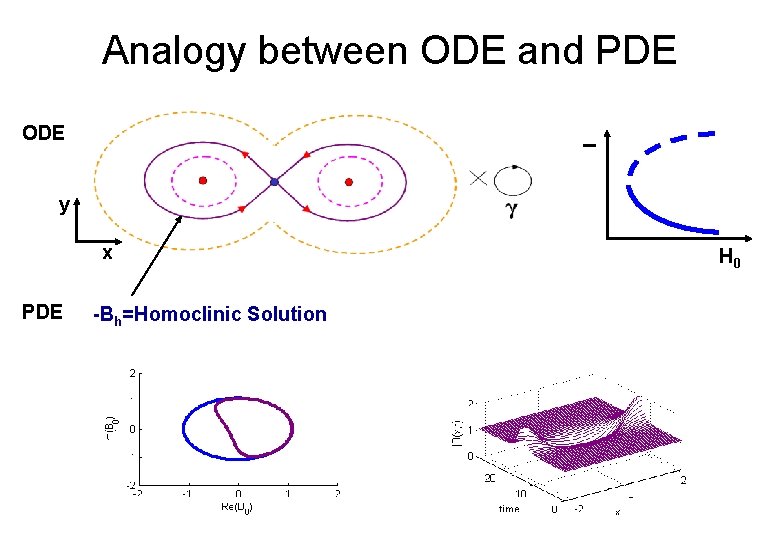
Analogy between ODE and PDE I ODE y x PDE -Bh=Homoclinic Solution H 0

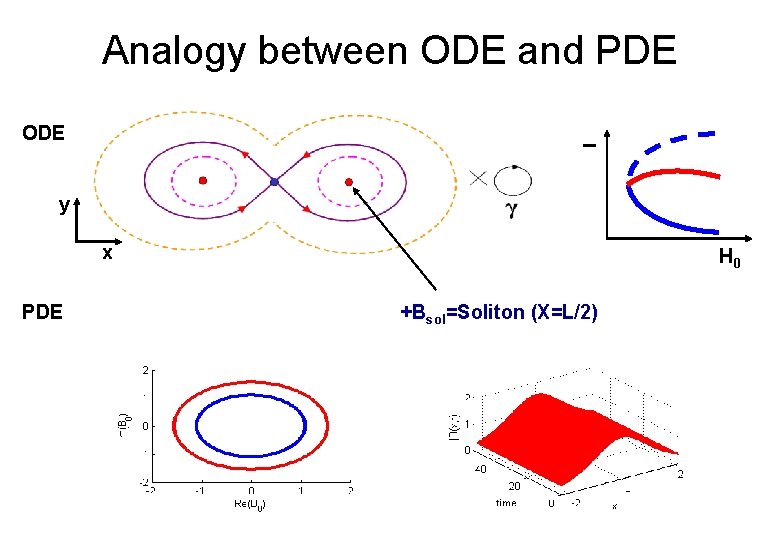
Analogy between ODE and PDE I ODE y x PDE H 0 +Bsol=Soliton (X=L/2)

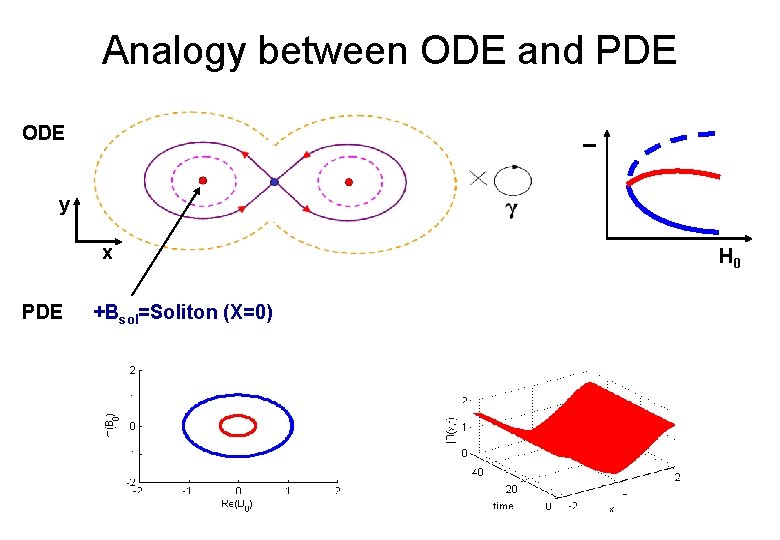
Analogy between ODE and PDE I ODE y x PDE +Bsol=Soliton (X=0) H 0

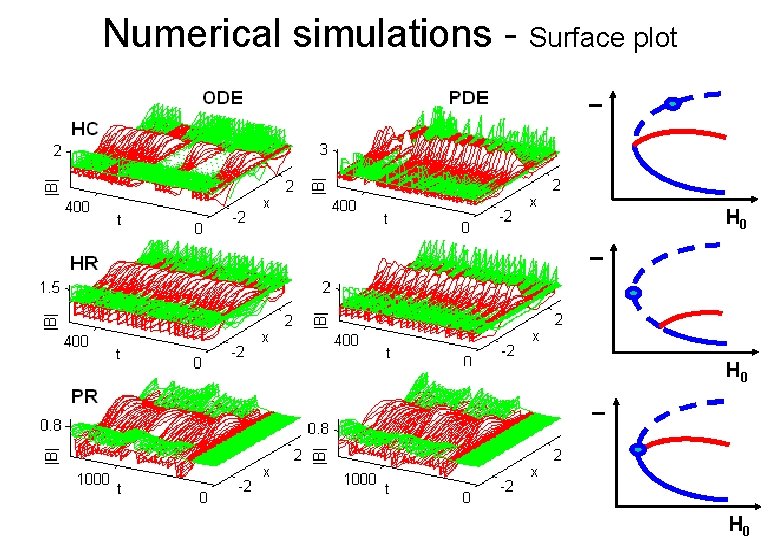
I Numerical simulations - Surface plot I H 0 H 0

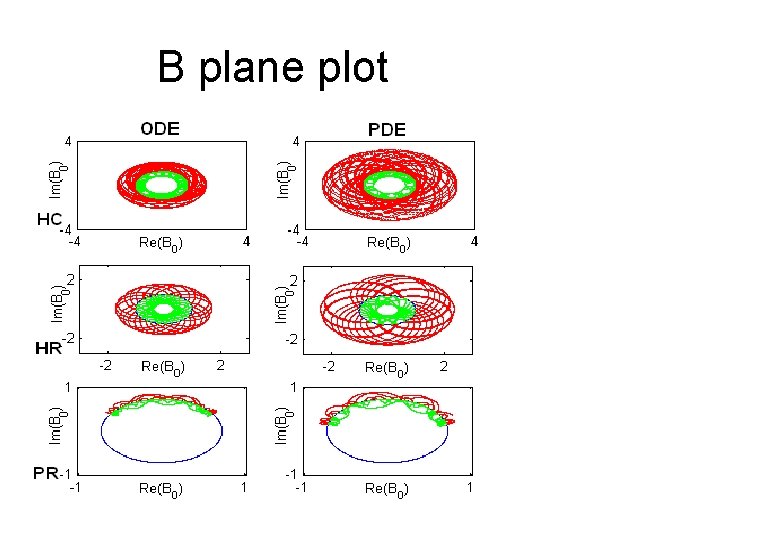
B plane plot

EMBD

I-γ plot

Conclusions • Three different types of chaotic behavior and instabilities in Hamiltonian perturbations of the NLS are described. • The study reveals a new type of behavior near the plane wave solution: Parabolic Resonance. • Possible applications to Bose-Einstein condensate.

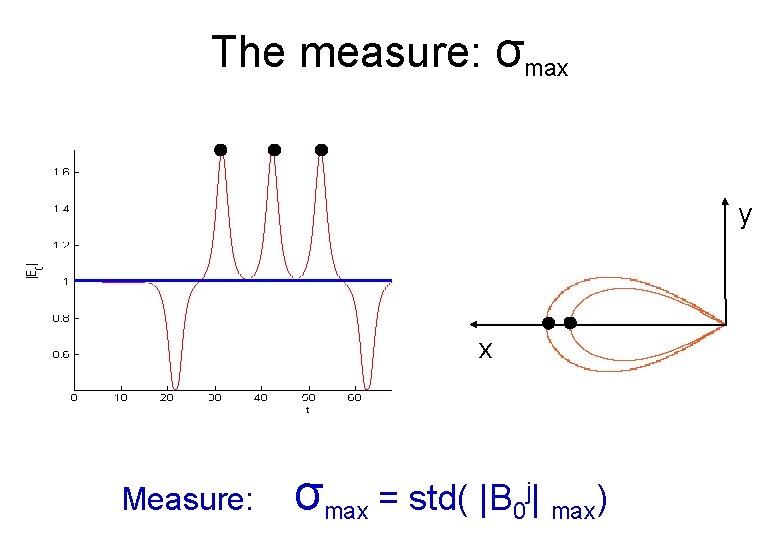
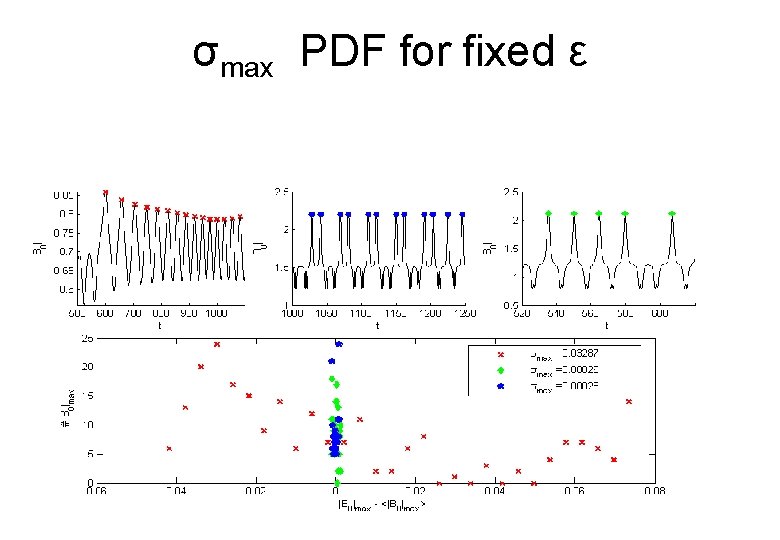
Characterization Tool • An input: Bin(x, t) – can we place this solution within our classification? • Quantitative way for classification (tool/measure) HC - O(ε), HR - O(ε 1/2), PR - O(ε 1/3) • Applying measure to PDE results

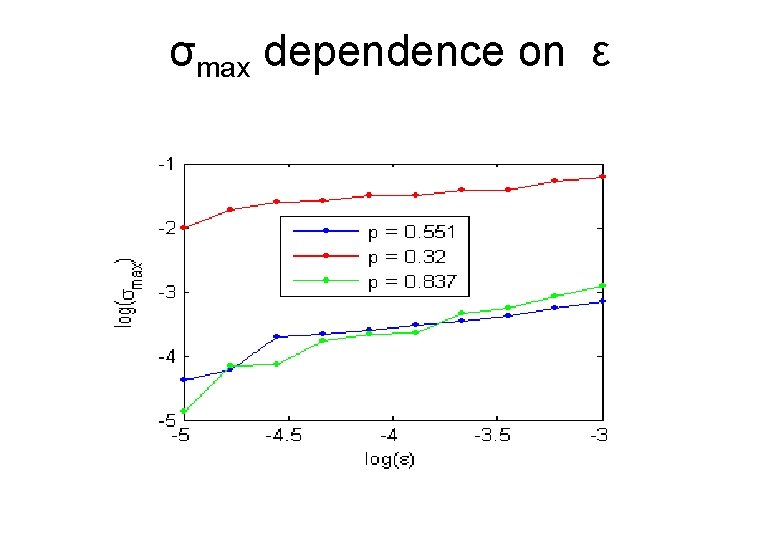
The measure: σmax y x Measure: σmax = std( |B 0 j| max)

σmax PDF for fixed ε

σmax dependence on ε

Future Work • Capturing the system into PR by variation of the forcing • Instabilities in the BEC • Resonant surface waves

Thank you!

Summary • We analyzed the modal equations with the “Hierarchy of Bifurcations” • Established the analogy between ODE and PDE • Numerical simulations of instabilities • Characterization tool

I Analogy between ODE and PDE y H 0 x -Bsol=Soliton (X=L/2) Bpw=Plane wave -Bh=Homoclinic Solution +Bsol=Soliton (X=0) +Bh=Homoclinic Solution

The Hierarchy of Bifurcations We can construct the EMBD for all fixed points in the model:

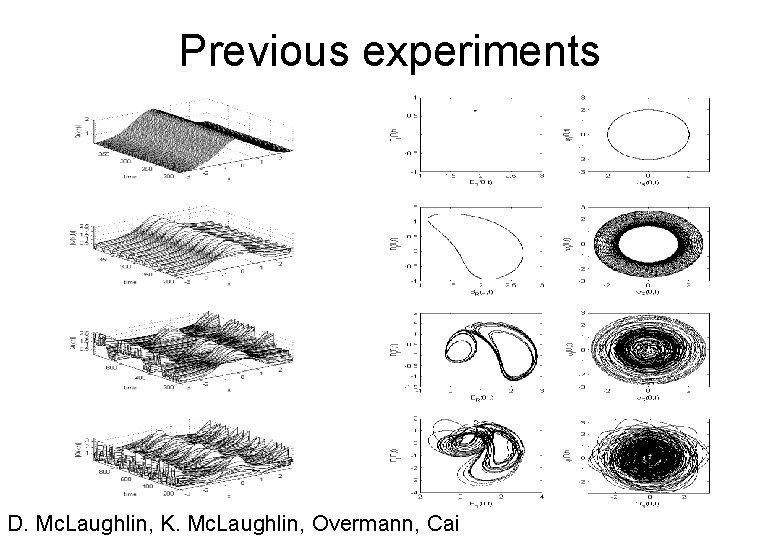
Previous experiments D. Mc. Laughlin, K. Mc. Laughlin, Overmann, Cai

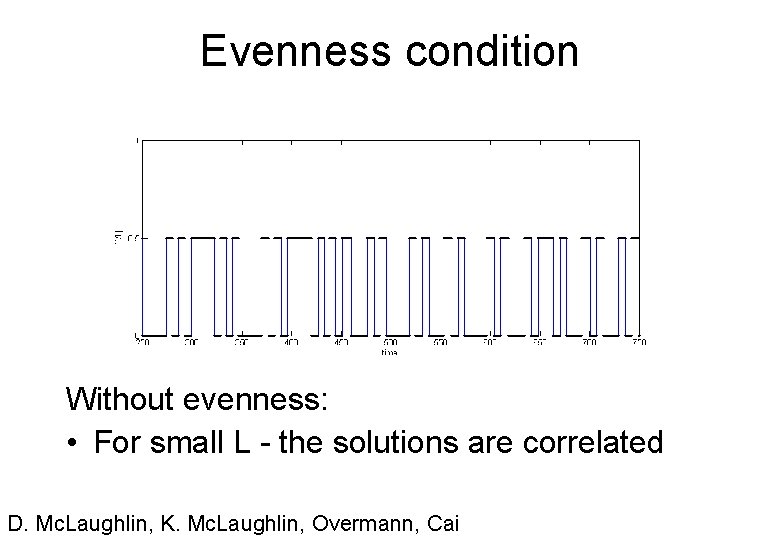
Evenness condition Without evenness: • For small L - the solutions are correlated D. Mc. Laughlin, K. Mc. Laughlin, Overmann, Cai

Local Stability • Plane wave: B(0, t)= c(t) • Introduce x-dependence of small magnitude B (x , t) = c(t) + b(x, t) • Plug into the integrable equation and solve the linearized equation. From dispersion relation get instability for: 0 < k 2 < |c|2

Local Stability • But k is discretized by L so kj = 2πj/L for j = 0, 1, 2… (j - number of LUMs) • Substitute to 0 < k 2 < |c|2 and get 2πj/L < |c| < 2π(j+1)/L • As we increase the amplitude the number of LUMs grows.

Validity of the model • For plane wave (b=0): • Substituting the condition for |c| for 1 LUM: 2πj/L < |c| < 2π(j+1)/L j=1 • Then the 2 model is plausible for I < 2 k 2

Analogy between ODE and PDE • Constants of motion • The solution