Mathematics for Computer Science MIT 6 042 J18

Mathematics for Computer Science MIT 6. 042 J/18. 062 J Graphs Copyright © Radhika Nagpal, 2002. Prof. Albert Meyer & Dr. Radhika Nagpal February 25, 2002 1

Connectivity • Are two vertices connected? Is there a path from one vertex to another? • How many paths are there from u to v • … February 25, 2002 2

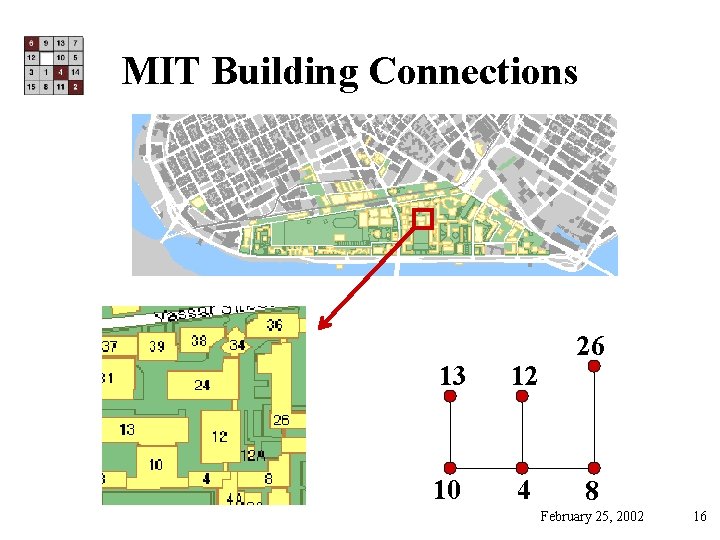
Example: MIT Buildings • Already saw one example last week • Can we get from one building to another without going outside? • = is the graph one connected component? • = is the transitive closure =? Vx. V February 25, 2002 3

Smallest Connected Graph • Question: repeat last part of MIT connected buildings question. • Ask how many people did this question? Answer: n-1 edges, now we can prove it February 25, 2002 4

Smallest Connected Graph • • What does this Graph look like? One answer: line Actually any tree ! Lots of choices, could easily optimize for something, e. g. congestion vs shortest distance between nodes (e. g star formation) February 25, 2002 5

Trees Definitions: • A connected graph with no cycles • A connected graph where |E| = |V| – 1 • A connected acyclic graph • A connected graph where removing an edge leaves a disconnected graph • There exists a unique simple path between any two vertices February 25, 2002 6

In class exercise: isomorphism and connectedness false proof. February 25, 2002 7

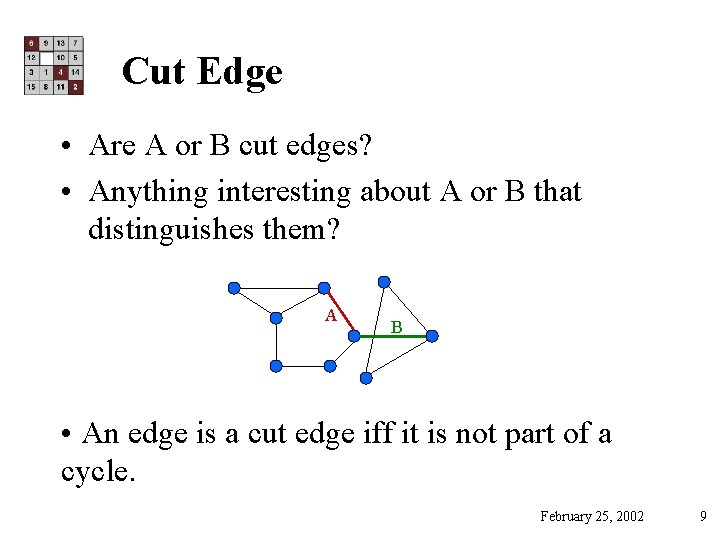
Cut Edge • Not only concerned with whether something is connected but also how easy is it to disconnect it? Fault-tolerance • Definition: An edge is a cut edge if removing it from the graph disconnects two connected components February 25, 2002 8

Cut Edge • Are A or B cut edges? • Anything interesting about A or B that distinguishes them? A B • An edge is a cut edge iff it is not part of a cycle. February 25, 2002 9

Discussion of False Proof Counter Example February 25, 2002 10

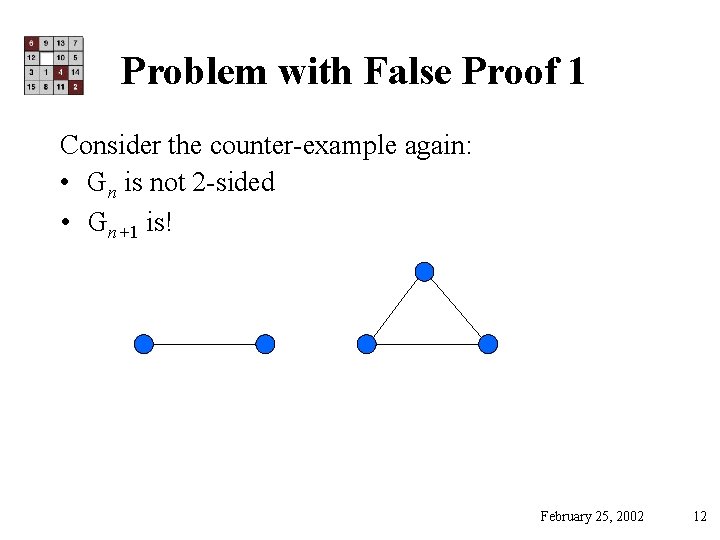
Problem with False Proof 1 Recall the induction axiom, What is R(n) here? R(n): = Gn is 2 -ended Gn is isomorphic to Ln Proof (silently) assumes the only way to get 2 -ended Gn+1 is to start with 2 -ended Gn. This isn’t true! February 25, 2002 11

Problem with False Proof 1 Consider the counter-example again: • Gn is not 2 -sided • Gn+1 is! February 25, 2002 12

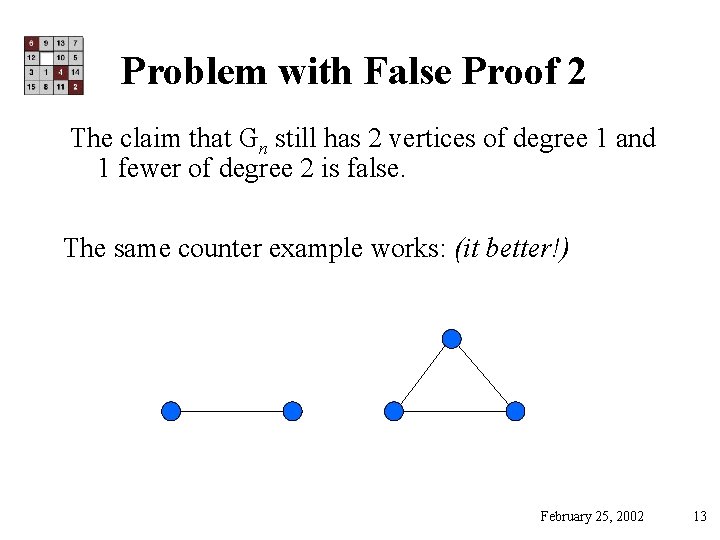
Problem with False Proof 2 The claim that Gn still has 2 vertices of degree 1 and 1 fewer of degree 2 is false. The same counter example works: (it better!) February 25, 2002 13

Discussion of cut-edge • Use this theorem on particular graphs • In a tree, every edge is a cut edge • In a mesh, no edge is a cut edge February 25, 2002 14

Old slides 1 February 25, 2002 15

MIT Building Connections 13 12 10 4 26 8 February 25, 2002 16

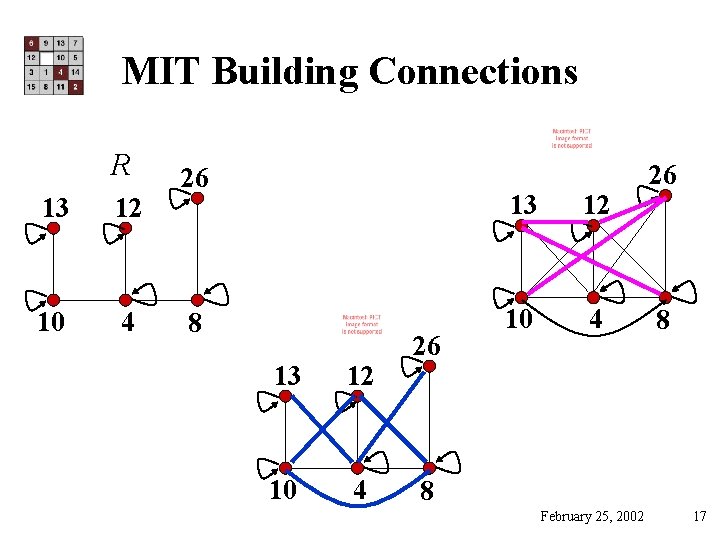
MIT Building Connections R 13 12 10 4 26 8 8 February 25, 2002 17

Composition using Matrices R 0 0 1 0 0 0 S 1 0 0 0 0 T 0 0 1 = 1 0 0 0 0 1 February 25, 2002 18

Composition and Path Lengths • is the set of all pairs (a, b) such that bldg a and b are connected via < 1 other bldg • In general is the set of all pairs (a, b) such that bldg a and b are connected via < k-1 other bldgs. – Prove using induction – Note: different if edges are not bidirectional February 25, 2002 19