Mathematics for Computer Science MIT 6 042 J18

Mathematics for Computer Science MIT 6. 042 J/18. 062 J Combinatorics I Copyright © Radhika Nagpal, 2002. Prof. Albert Meyer & Dr. Radhika Nagpal March 17, 2002 1

Counting Techniques • • • Bijections Sum Rule, Inclusion-Exclusion Product Rule Pigeonhole Principle Trees Permutations March 17, 2002 2

Counting Strings • How many strings of length 3 can make with the alphabet A = {r, a, d} ? March 17, 2002 3

Counting Strings (3) (3) {r, a, d} Number of strings = 3. 3. 3 = 27 March 17, 2002 4

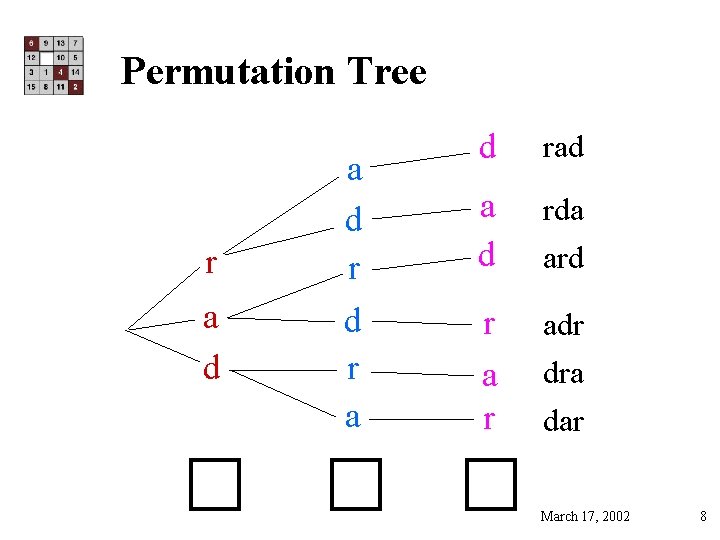
Counting Rearrangements • How many strings of length 3 can I make by rearranging the letters rad? March 17, 2002 5

Permutations (3) (2) {r, a, d} {? , ? } (1) {? } Number of strings, |S| = 3. 2. 1 = 6 March 17, 2002 6

Permutations (3) (2) {r, a, d} {? , ? } S = {rad, rda ard, adr dra, dar} (1) {? } March 17, 2002 7

Permutation Tree r a d r d r a d rad a d rda ard r adr dra dar March 17, 2002 8

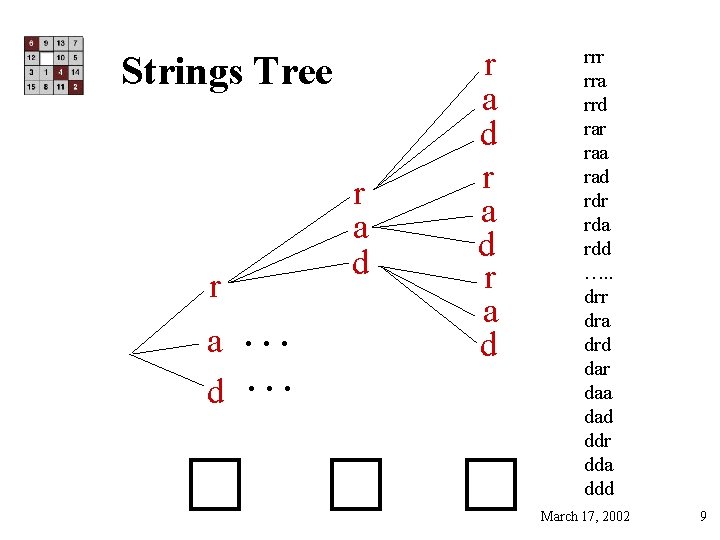
Strings Tree r a d … … r a d rrr rra rrd rar raa rad rdr rda rdd …. . drr dra drd dar daa dad ddr dda ddd March 17, 2002 9

Comparison rearrangement strings nn n n 2 n! 1 1 5 25 120 3125 10 100 ~107 1010 20 400 ~1018 1026 40 1600 ~1047 1064 10000 ~10157 10200 106 scheme dies…. . March 17, 2002 10

Important technique: Matching • Make a one-to-one mapping between a given problem and a set of known cardinality (or at least one we know how to count…) Functions Lists Graphs, Relations Strings, Polynomials Binary strings Trees Matrices Balls and Bins March 17, 2002 11

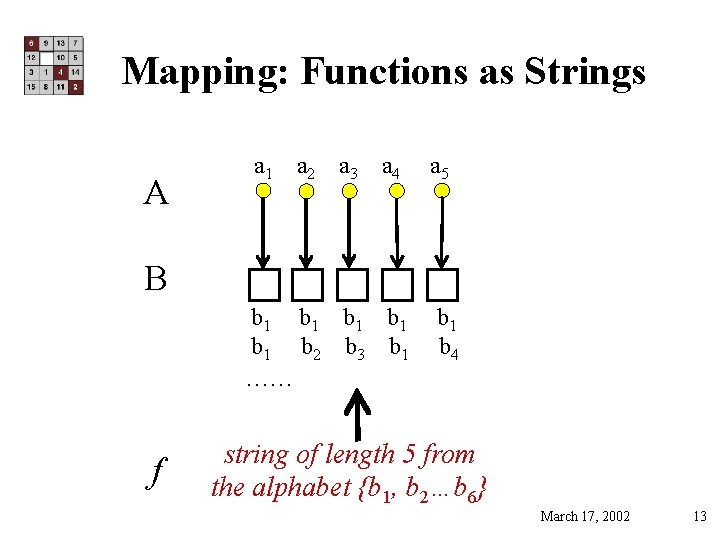
Counting Functions • How many different possible functions are there from A to B? f A a 1 a 2 a 3 a 4 a 5 b 1 b 2 b 3 b 4 b 5 b 6 B March 17, 2002 12

Mapping: Functions as Strings A a 1 a 2 a 3 a 4 a 5 B b 1 b 1 b 1 b 2 b 3 b 1 …… f b 1 b 4 string of length 5 from the alphabet {b 1, b 2…b 6} March 17, 2002 13

Counting Functions A a 1 a 2 a 3 a 4 a 5 B (6) (6) (6) Total number of possible functions = total number of possible strings = 6. 6. 6 = March 17, 2002 14

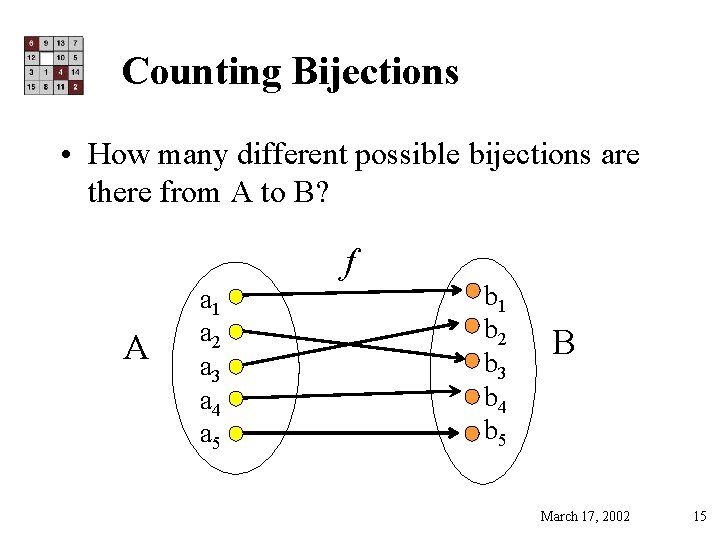
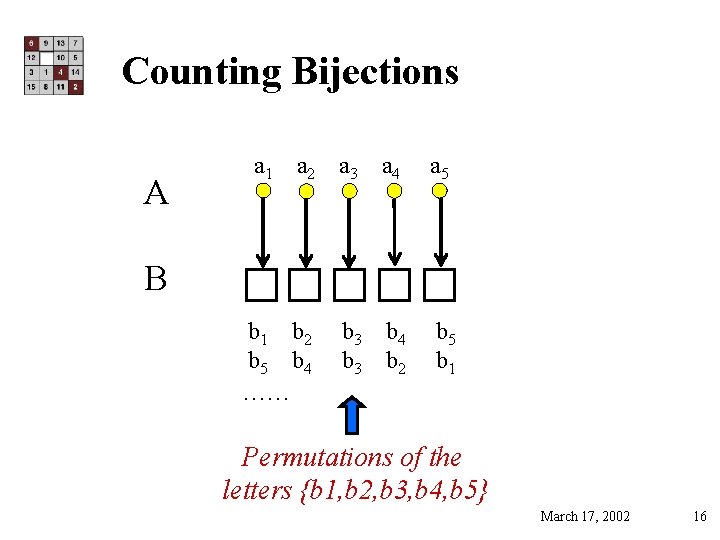
Counting Bijections • How many different possible bijections are there from A to B? f A a 1 a 2 a 3 a 4 a 5 b 1 b 2 b 3 b 4 b 5 B March 17, 2002 15

Counting Bijections A a 1 a 2 a 3 a 4 a 5 B b 1 b 2 b 5 b 4 …… b 3 b 4 b 3 b 2 b 5 b 1 Permutations of the letters {b 1, b 2, b 3, b 4, b 5} March 17, 2002 16

Counting Bijections A a 1 a 2 a 3 a 4 a 5 B (5) (4) (3) (2) (1) Total number of possible functions = total number of possible permutations = 5. 4. 3. 2. 1 = 5! March 17, 2002 17

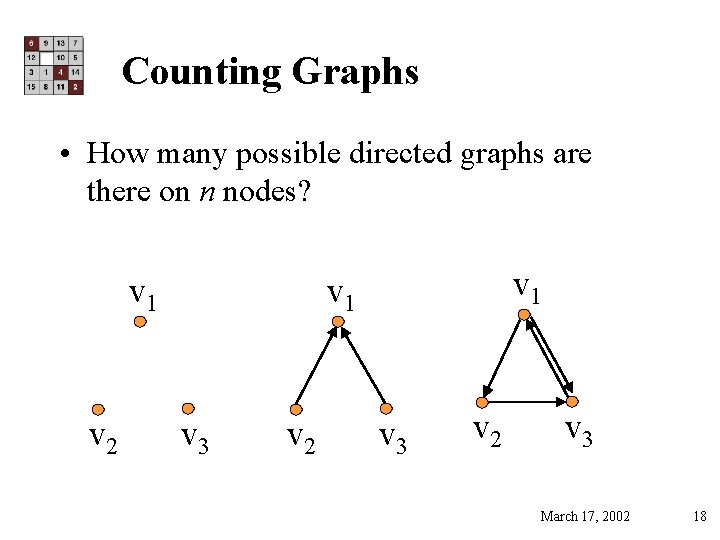
Counting Graphs • How many possible directed graphs are there on n nodes? v 1 v 2 v 1 v 3 v 2 v 3 March 17, 2002 18

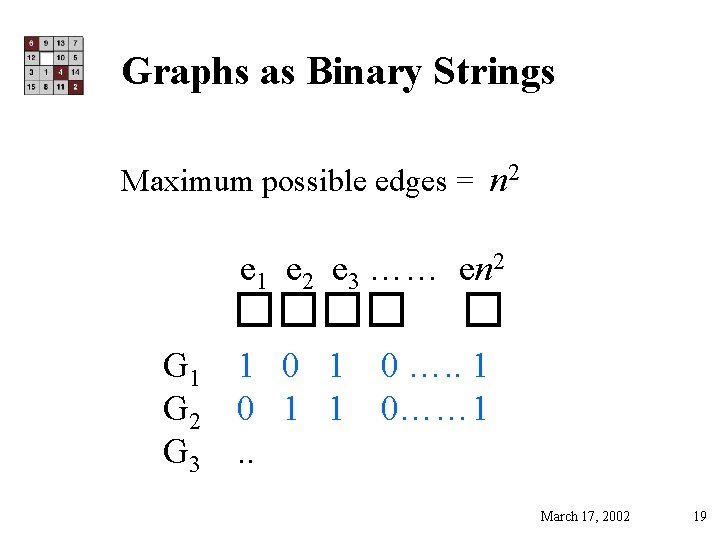
Graphs as Binary Strings Maximum possible edges = n 2 e 1 e 2 e 3 …… en 2 G 1 1 0 1 G 2 0 1 1 G 3. . 0 …. . 1 0…… 1 March 17, 2002 19

Graphs as Boolean Matrices 1 2 3 …. 1 1 0 1 2 0 1 3 0 1. . n n Any assignment of 1 s and 0 s is a possible graph March 17, 2002 20

Proving that a Mapping is a Bijection • Prove that g: F S is a bijection – Prove that all elements in F map to a unique elements of S – Prove that all elements in S map to some F March 17, 2002 21

Example: Graph Isomorphism • G 1 and G 2 are isomorphic if there is a bijection f from the nodes of G 1 to the nodes of G 2, that preserve the adjacency lists. • Question: At most how many functions do I need to check to determine whether or not G 1 and G 2 are isomorphic? • Answer: All possible bijections from the nodes of G 1 to G 2 = n! March 17, 2002 22

In-class Problems March 17, 2002 23