MATH 2306 History of Mathematics Instructor Dr Alexandre

COURSE OUTLINE • • Theorem of Pythagoras (Ch. 1) Greek Geometry (Ch. 2) Greek

Chapter 1 Theorem of Pythagoras • • Arithmetic and Geometry Pythagorean Triples Rational Points

1. 1 Arithmetic and Geometry Theorem of Pythagoras If c is the hypotenuse of

Remarks • Converse statement: if a, b and c satisfy a 2+b 2=c 2

1. 2 Pythagorean Triples • Definition Integer triples (a, b, c) satisfying a 2+b

• Diophantine equation (after Diophantus, 300 CE) - polynomial equation with integer coefficients

General Formula • Theorem Any Pythagorean triple can be obtained as follows: a =

1. 3 Rational Points on the Circle • Pythagorean triple (a, b, c) •

Construction of rational points on the circle • Base point (trivial solution) Q(x, y)

c 2 of Pythagoras’ Triangles Theorem 1. 4 Proof Right-angled a 2 a c

1. 5 Irrational Numbers • For Pythagoreans “a number” meant integer • The ratio

Consequences of this discovery • According to the legend, first Pythagorean to make the

1. 6 The Definition of Distance • Coordinates of a point on the plane:

1. 7 Biographical Notes: Pythagoras • Born on island Samos • Learned mathematics from

Slides: 16

Download presentation

MATH 2306 History of Mathematics Instructor: Dr. Alexandre Karassev

COURSE OUTLINE • • Theorem of Pythagoras (Ch. 1) Greek Geometry (Ch. 2) Greek Number Theory (Ch. 3) Infinity in Greek Mathematics (Ch. 4) } Greek Mathematics (≈ 300 BCE – 250 CE) • Number Theory in Asia (Ch. 5) } China and India (≈ 300 -1200 CE) • Polynomial Equations (Ch. 6) • • • Calculus (Ch. 9) Infinite Series (Ch. 10) The Number Theory Revival (Ch. 11) • Complex Numbers in Algebra (Ch. 14) } Europe (17 th – 18 th century CE)

Chapter 1 Theorem of Pythagoras • • Arithmetic and Geometry Pythagorean Triples Rational Points on the Circle Right-angled Triangles Irrational Numbers The Definition of Distance Biographical Notes: Pythagoras

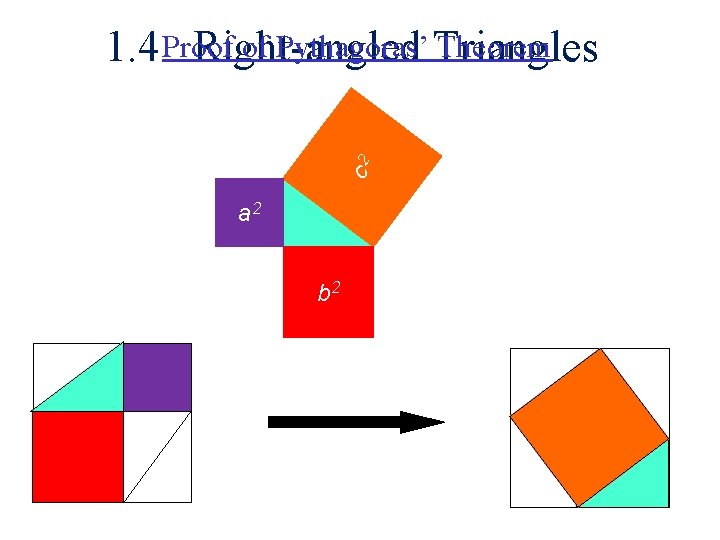
1. 1 Arithmetic and Geometry Theorem of Pythagoras If c is the hypotenuse of a right-angled triangle and a, b are two other sides then a 2 + b 2 = c 2 a 2+b 2=c 2 “Let no one unversed in geometry enter here” c 2 was written over the door of Plato’s Academy (≈ 387 BCE) a 2 b 2

Remarks • Converse statement: if a, b and c satisfy a 2+b 2=c 2 then there exists a right-angled triangle with corresponding sides. • One can consider a 2+b 2=c 2 as an equation • It has some simple solutions: (3, 4, 5), (5, 12, 13) etc. • Practical use - construction of right angles • Deep relationship between arithmetic and geometry • Discovery of irrational numbers

1. 2 Pythagorean Triples • Definition Integer triples (a, b, c) satisfying a 2+b 2=c 2 are called Pythagorean triples • Examples: (3, 4, 5), (5, 12, 13), (8, 15, 17) etc. • Pythagoras: around 500 BCE • Babylonia 1800 BCE: clay tablet “Plimpton 322” lists integer pairs (a, c) such that there is an integer b satisfying a 2+b 2=c 2 • China (200 BCE -220 CE), India (500 -200 BCE) • Greeks: between Euclid (300 BCE) and Diophantus (250 CE)

• Diophantine equation (after Diophantus, 300 CE) - polynomial equation with integer coefficients to which integer solutions are sought • It was shown that there is no algorithm for deciding which polynomial equations have integer solutions.

General Formula • Theorem Any Pythagorean triple can be obtained as follows: a = (p 2 -q 2)r, b = 2 qpr, c = (p 2+q 2)r where p, q and r are arbitrary integers. • Special case: a = p 2 -q 2, b = 2 qp, c = p 2+q 2 • Proof of general formula: Euclid’s “Elements” Book X (around 300 BCE)

1. 3 Rational Points on the Circle • Pythagorean triple (a, b, c) • Triangle with rational sides x = a/c, y = b/c and hypotenuse c = 1 • x 2 + y 2 = 1 → P (x, y) is a rational point on the unit circle. Y P 1 O x y X

Construction of rational points on the circle • Base point (trivial solution) Q(x, y) = (-1, 0) • Line through Q with rational slope t y = t(x+1) intersects the circle at a second rational point R • As t varies we obtain all rational points on the Y circle which have the form R x = (1 -t 2) / (1+t 2), y = 2 t / (1+t 2) where t = p/q Q X -1 O 1

c 2 of Pythagoras’ Triangles Theorem 1. 4 Proof Right-angled a 2 a c b b 2

1. 5 Irrational Numbers • For Pythagoreans “a number” meant integer • The ratio between two such numbers is a rational number • According to the Pythagoras theorem, the diagonal of the unit square is not a rational number • Discovery of incommensurable lengths (not measurable as integer multiple of the same unit) • Irrational numbers 1 1

Consequences of this discovery • According to the legend, first Pythagorean to make the discovery public was drowned at sea • Split between Greek theories of number and space • Greek geometers developed techniques allowing to avoid the use of irrational numbers (theory of proportions and the method of exhaustion)

1. 6 The Definition of Distance • Coordinates of a point on the plane: pair of numbers (x, y) • Development of analytic geometry (17 th CE) • Notion of distance Y P R y O x P Y X O ? X

Y P (x 2 , y 2 ) x 2 -x 1 R (x 1 , y 1 ) Pythagoras’ theorem: y 2 -y 1 X O Alternative approach: Definition A point is an ordered pair (x, y) Distance between two points R (x 1 , y 1 ) and P (x 2 , y 2 ) is defined by formula

1. 7 Biographical Notes: Pythagoras • Born on island Samos • Learned mathematics from Thales (624 - 547 BCE) (Miletus) • Croton (around 540 BCE) • Founded a school (Pythagoreans) – “All is number” – strict code of conduct (secrecy, vegetarianism, taboo on eating beans etc. ) – explanation of musical harmony in terms of whole-number ratios Pythagoras (580 BCE – 497 BCE)