Matemtica para Economia III 2013 2 Aula 13

Matemática para Economia III 2013. 2 Aula 13 e 14: Transformações lineares (continuação)/ Autovalores e Autovetores/ Diagonalização de Operadores

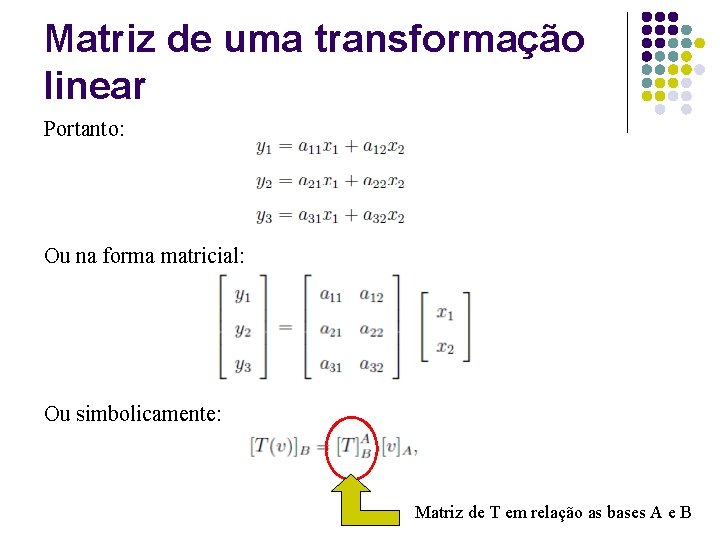
Matriz de uma transformação linear Sejam T: V→W uma transformação linear, A uma base de V e B uma base de W. Sem perda de generalidade consideremos dim V=2 e dim W=3. Sejam A={v 1, v 2} e B={w 1, w 2, w 3}, um vetor v ϵ V pode ser expresso como (1) Note que [v]A=(x 1, x 2) A imagem T(v) ϵ W pode ser expressa como (2) Note que [T(v)]B=(y 1, y 2, y 3) Por outro lado aplicando T em (1) obtemos (3)

Matriz de uma transformação linear Sendo T(v 1) e T(v 2) ϵ W eles são combinações lineares dos vetores de B: (4) (5) Substituindo em (3) temos que

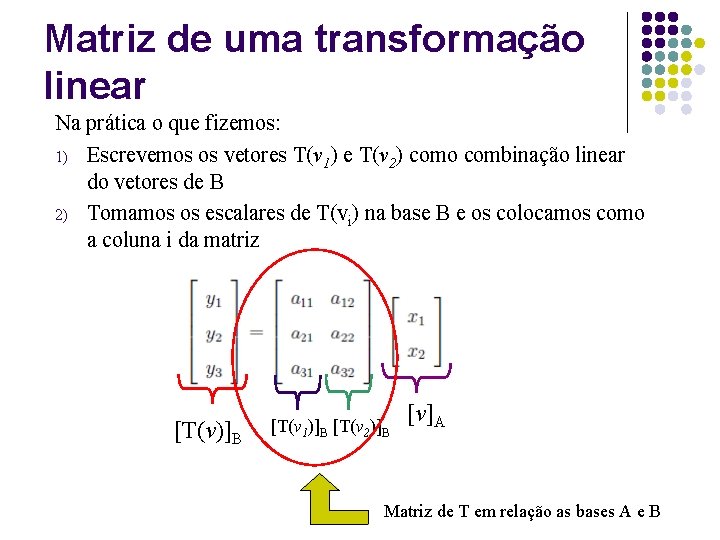
Matriz de uma transformação linear Portanto: Ou na forma matricial: Ou simbolicamente: Matriz de T em relação as bases A e B

Matriz de uma transformação linear Na prática o que fizemos: 1) Escrevemos os vetores T(v 1) e T(v 2) como combinação linear do vetores de B 2) Tomamos os escalares de T(vi) na base B e os colocamos como a coluna i da matriz [T(v)]B [T(v 1)]B [T(v 2)]B [v]A Matriz de T em relação as bases A e B

Matriz de uma transformação linear Exemplo: Dada a transformação linear T: IR 2→IR 3 dada por T(x, y)=(x+y, x-y, y), E considere as bases A={(1, 1), (-1, 0)} e B={(1, 0, 0), (0, 1, 0), (0, 0, 1)} para o IR 2 e IR 3 respectivamente. Determine: a) b) Sendo v=(5, 1) (coordenadas em relação à base canônica do IR 2), calcular [T(v)]B utilizando a matriz encontrada em a)

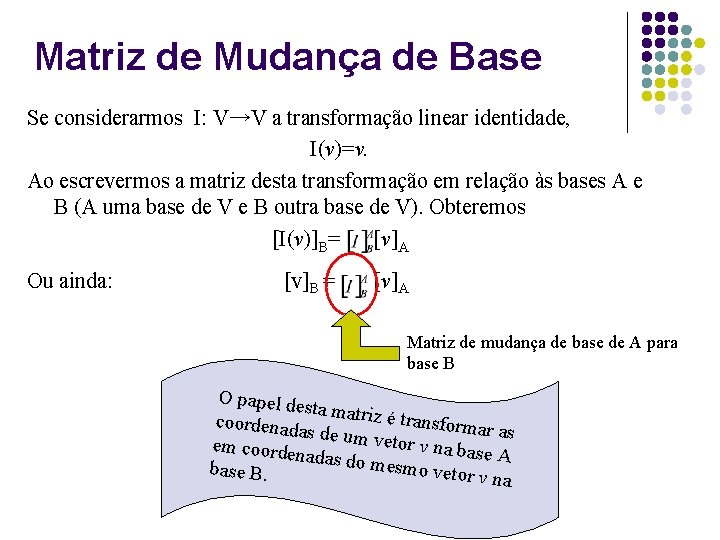
Matriz de Mudança de Base Se considerarmos I: V→V a transformação linear identidade, I(v)=v. Ao escrevermos a matriz desta transformação em relação às bases A e B (A uma base de V e B outra base de V). Obteremos [I(v)]B= [v]A Ou ainda: [v]B = [v]A Matriz de mudança de base de A para base B O papel de sta matriz é transform coordenad ar as as de um v e tor v na ba em coorde se A nadas do m e smo vetor base B. v na

Autovetores e Autovalores Seja T: V→V um operador linear. Um vetor v ϵ V, v≠ 0, é autovetor do operador T se existe λ ϵ IR tal que (6) T(v)= λv. Seja M a matriz desta transformação em relação à base canônica então (6) pode ser rescrito como Mv=λv λv-Mv=0 ou ainda λIv-Mv=0 (λI-M)v=0. (7) l l Determinar se operador T possui um autovetor v≠ 0 equivale a determinar para quais valores de λ o sistema homogêneo (7) tem solução não trivial, tal valor de λ é chamado autovalor de M. Se λ é um autovalor de M então cada solução não trivial de (7) será o autovetor de M associado ao autovalor λ, ou seja será autovetor do operador T.

Autovetores e Autovalores De acordo com o que já estudamos M é invertível ↔ Mv=0 tem somente solução trivial logo (λI-M)v=0 tem solução não trivial ↔ (λI-M) não é invertível, ou seja, det(λI-M)=0 Exemplo: (b) Seja M=[T], encontre os autovalores de M e dê exemplo de autovetores associados a cada autovalor

Autovetores e Autovalores Teorema: Se A é uma matriz nxn, então as seguintes afirmações são equivalentes: a) A é invertível. b) Ax=0 só tem a solução trivial. c) A forma escalonada reduzida por linhas de A é In. d) A pode ser expressa como um produto de matrizes elementares. e) Ax=b é consistente para cada vetor coluna b de tamanho nx 1. f) Ax=b tem exatamente uma solução para cada vetor coluna b nx 1. g) det(A)≠ 0. h) A tem posto n. i) As linhas de A formam um conjunto L. I. de n vetores do IRn. j) As colunas de A formam um conjunto L. I. de n vetores do IRn. k) Zero não é um autovalor de A.

Diagonalização de operadores Seja T: V→ V um operador linear. Dizemos que T é um operador diagonalizável se existe uma base β de V cujos elementos são autovetores de T. A matriz que representa T na base β é uma matriz diagonal cujos elementos são os autovalores de T, ou seja:

Diagonalização de operadores Seja M=[T] a matriz canônica do operador T e D a matriz de T na base β de autovetores, dizemos que T é diagonalizável se existe uma matriz P tal que D = P– 1 MP. Onde P é a matriz cujas colunas são os autovetores de T e D=[T]β. Assim, a matriz D é obtida pela matriz P, quando ela existe, sobre a matriz M. Dizemos então que a matriz P diagonaliza M ou que P é a matriz diagonalizadora (P a matriz de mudança da base canônica para base de β). l Quando sabemos que é possível encontrar a matriz P e obter D?

Diagonalização de operadores Teorema: Se M=[T] possui todas as raízes de seu polinômio característico reais e distintas então M é diagonalizável. Obs: raízes do polinômio característico reais e distintas autovetores associados a autovalores distintos são L. I existe uma base de autovetores para V Temos o seguinte resultado para matrizes simétricas: Teorema: Se M é uma matriz simétrica de ordem n então existe uma matriz ortogonal P tal que P– 1 MP=D, D uma matriz diagonal. Os autovalores de M são elementos da diagonal D. (Lembrete: Matriz ortogonal P-1=PT).

Diagonalização de operadores Exemplo: