MACHINE LEARNING CMPT 726 SIMON FRASER UNIVERSITY CHAPTER

MACHINE LEARNING CMPT 726 SIMON FRASER UNIVERSITY CHAPTER 1: INTRODUCTION

Outline • Comments on general approach. • Probability Theory. • Joint, conditional and marginal probabilities. • Random Variables. • Functions of R. V. s • Bernoulli Distribution (Coin Tosses). • Maximum Likelihood Estimation. • Bayesian Learning With Conjugate Prior. • The Gaussian Distribution. • Maximum Likelihood Estimation. • Bayesian Learning With Conjugate Prior. • More Probability Theory. • Entropy. • KL Divergence.

Our Approach • The course generally follows statistics, very interdisciplinary. • Emphasis on predictive models: guess the value(s) of target variable(s). “Pattern Recognition” • Generally a Bayesian approach as in the text. • Compared to standard Bayesian statistics: • more complex models (neural nets, Bayes nets) • more discrete variables • more emphasis on algorithms and efficiency

Things Not Covered • Within statistics: • Hypothesis testing • Frequentist theory, learning theory. • Other types of data (not random samples) • Relational data • Scientific data (automated scientific discovery) • Action + learning = reinforcement learning. Could be optional – what do you think?

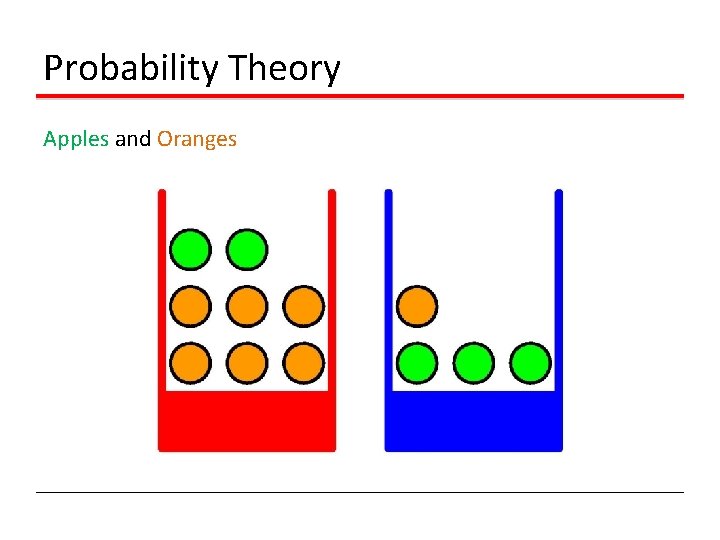
Probability Theory Apples and Oranges

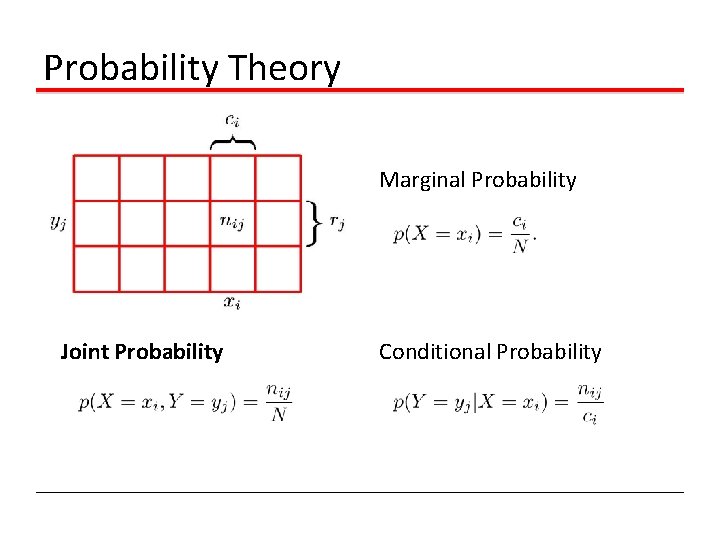
Probability Theory Marginal Probability Joint Probability Conditional Probability

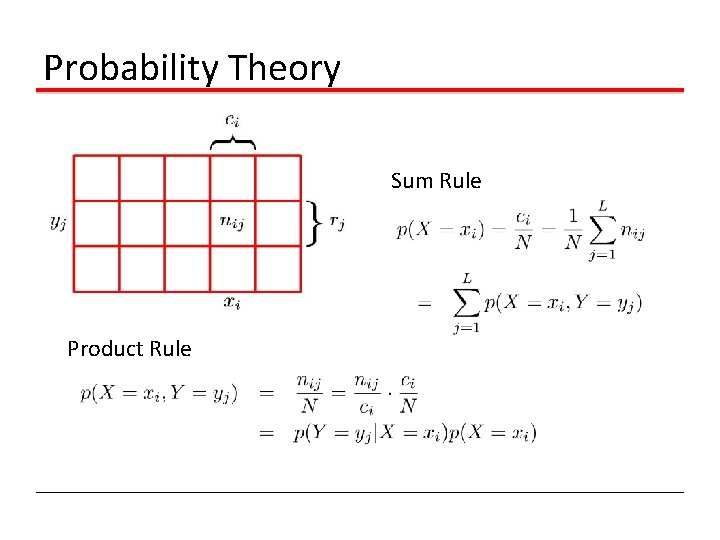
Probability Theory Sum Rule Product Rule

The Rules of Probability Sum Rule Product Rule

Bayes’ Theorem posterior likelihood × prior

Bayes’ Theorem: Model Version • Let M be model, E be evidence. • P(M|E) proportional to P(M) x P(E|M) Intuition • prior = how plausible is the event (model, theory) a priori before seeing any evidence. • likelihood = how well does the model explain the data?

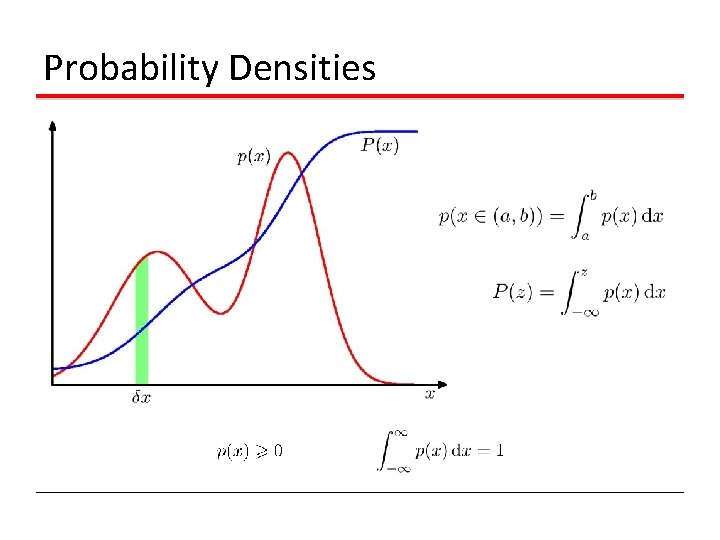
Probability Densities

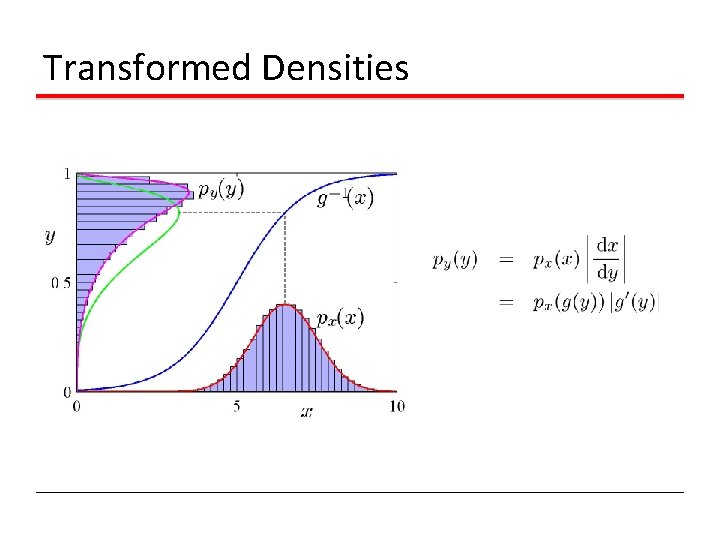
Transformed Densities

Expectations Conditional Expectation (discrete) Approximate Expectation (discrete and continuous)

Expectations are Linear • Let a. X + b. Y + c be a linear combination of two random variables (itself a random variable). • Then E[a. X + b. Y + c] = a. E[X] + b. E[Y] + c. • This holds whether or not X and Y are independent. • Good exercise to prove it.

Variances and Covariances Think about this difference: 1. Everybody gets a B. 2. 10 students get a C, 10 get an A. The average is the same – how to quantify the difference? Prove this. Hint: use the linearity of expectation.