LIMITS oh yeah Calculus has its limits AP

LIMITS … oh yeah, Calculus has its limits! AP CALCULUS MS. OLIFER

What you’ll learn about • Definition of Limit • Properties of Limits • One-Sided and Two-Sided Limits …and why Limits can be used to describe continuity, the derivative and the integral: the ideas giving the foundation of calculus.

Definition of Limit Example 1, pg. 69

Definition of Limit continued

Theorem 1 • For any constant k and c, Slide 2 - 5

One-Sided and Two-Sided Limits

One-Sided and Two-Sided Limits continued

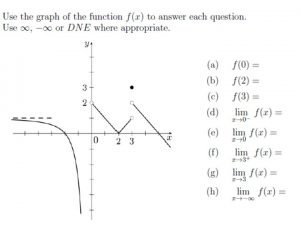
Example One-Sided and Two-Sided Limits Find the following limits from the given graph. 4 o 1 2 3

Limits: A Numerical and Graphical Approach THEOREM: As x approaches a, the limit of f (x) is L, if the limit from the left exists and the limit from the right exists and both limits are L. That is, if 1) and 2) then

Limits: A Numerical and Graphical Approach Example 1: Consider the function H given by Graph the function, and find each of the following limits, if they exist. When necessary, state that the limit does not exist. a) b)

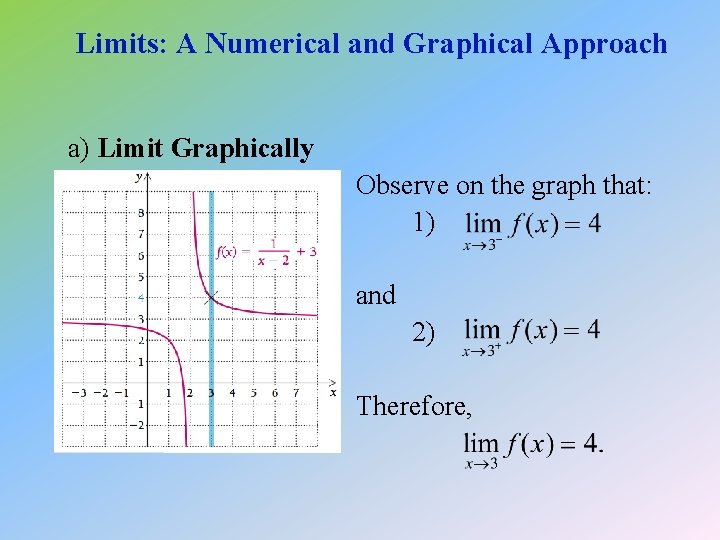
Limits: A Numerical and Graphical Approach a) Limit Numerically First, let x approach 1 from the left: H(x) 0 2 0. 5 3 Thus, it appears that 0. 8 3. 6 0. 9 3. 8 0. 99 3. 98 0. 999 3. 998

Limits: A Numerical and Graphical Approach a) Limit Numerically (continued) Then, let x approach 1 from the right: H(x) 2 0 1. 8 – 0. 4 Thus, it appears that 1. 1 – 1. 8 1. 01 1. 0001 – 1. 98 – 1. 9998

Limits: A Numerical and Graphical Approach a) Limit Numerically (concluded) Since 1) and 2) Then, does not exist.

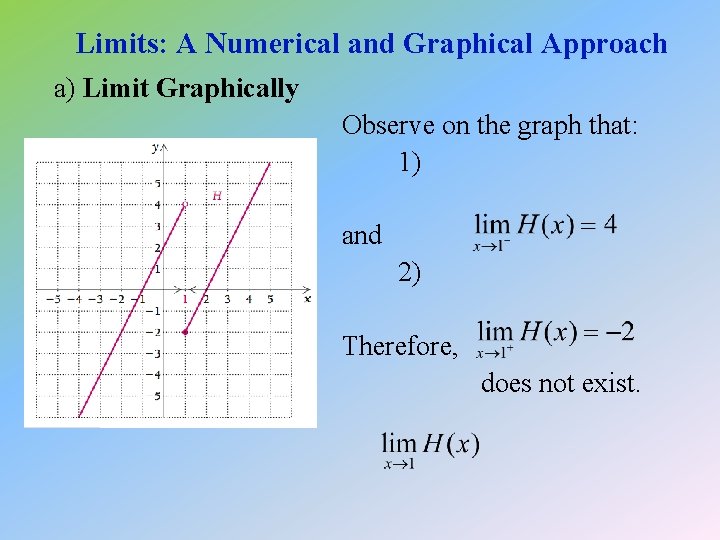
Limits: A Numerical and Graphical Approach a) Limit Graphically Observe on the graph that: 1) and 2) Therefore, does not exist.

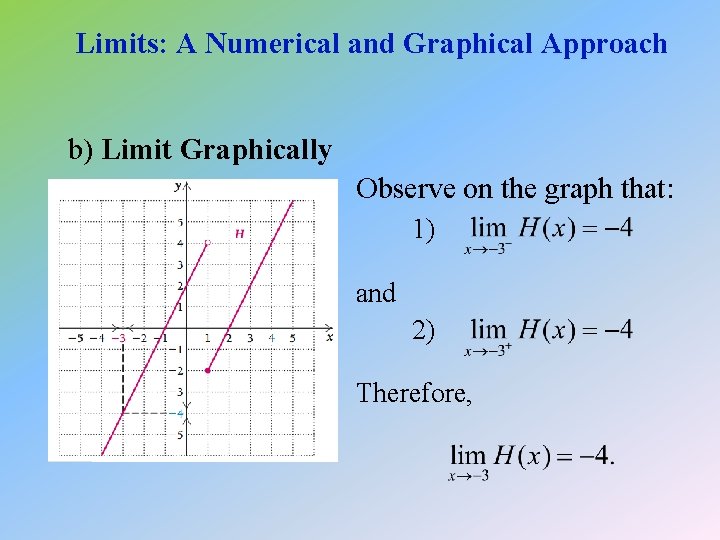
Limits: A Numerical and Graphical Approach b) Limit Numerically First, let x approach – 3 from the left: H(x) – 4 – 6 Thus, it appears that – 3. 5 – 3. 1 – 4. 2 – 3. 01 – 4. 02 – 3. 001 – 4. 002

Limits: A Numerical and Graphical Approach b) Limit Numerically (continued) Then, let x approach – 3 from the right: H(x) – 2 Thus, it appears that – 2. 5 – 3 – 2. 9 – 3. 8 – 2. 99 – 3. 98 – 2. 999 – 3. 998

Limits: A Numerical and Graphical Approach b) Limit Numerically (concluded) Since 1) and 2) Then,

Limits: A Numerical and Graphical Approach b) Limit Graphically Observe on the graph that: 1) and 2) Therefore,

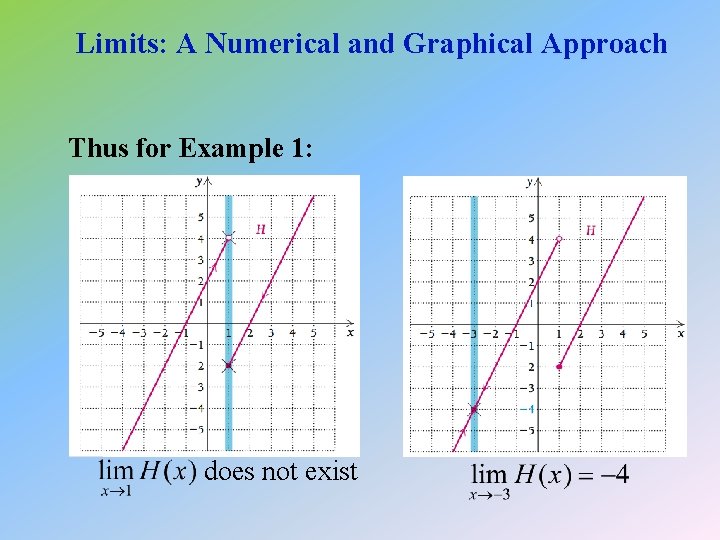
Limits: A Numerical and Graphical Approach The “Wall” Method: As an alternative approach to Example 1, we can draw a “wall” at x = 1, as shown in blue on the following graphs. We then follow the curve from left to right with pencil until we hit the wall and mark the location with an × , assuming it can be determined. Then we follow the curve from right to left until we hit the wall and mark that location with an ×. If the locations are the same, we have a limit. Otherwise, the limit does not exist.

Limits: A Numerical and Graphical Approach Thus for Example 1: does not exist

Limits: A Numerical and Graphical Approach Example 3: Consider the function f given by Graph the function, and find each of the following limits, if they exist. If necessary, state that the limit does not exist. a) b)

Limits: A Numerical and Graphical Approach a) Limit Numerically Let x approach 3 from the left and right: f (x) 2. 1 13 2. 5 5 2. 99 3. 5 3. 2 3. 1 3. 01 f (x) Thus,

Limits: A Numerical and Graphical Approach a) Limit Graphically Observe on the graph that: 1) and 2) Therefore,

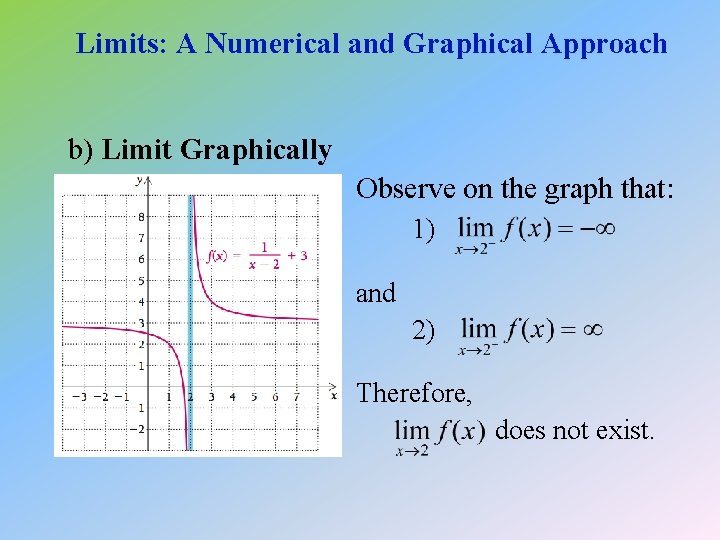
Limits: A Numerical and Graphical Approach b) Limit Numerically Let x approach 2 from the left and right: f (x) 1. 5 1 1. 9 – 7 1. 99 – 97 1. 999 – 997 f (x) 2. 5 5 2. 1 13 2. 01 103 2. 001 1003 Thus, does not exist.

Limits: A Numerical and Graphical Approach b) Limit Graphically Observe on the graph that: 1) and 2) Therefore, does not exist.

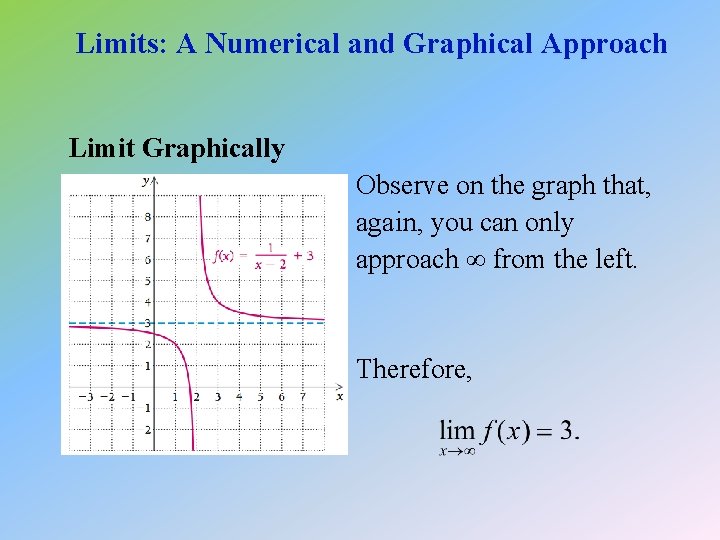
1. 1 Limits: A Numerical and Graphical Approach Example 4: Consider again the function f given by Find

Limits: A Numerical and Graphical Approach Limit Numerically Note that you can only approach ∞ from the left: 5 f (x) Thus, 10 1000 3. 125 3. 0102 3. 001

Limits: A Numerical and Graphical Approach Limit Graphically Observe on the graph that, again, you can only approach ∞ from the left. Therefore,

Properties of Limits

Properties of Limits continued Product Rule: Constant Multiple Rule:

Properties of Limits continued

Example Properties of Limits

Polynomial and Rational Functions

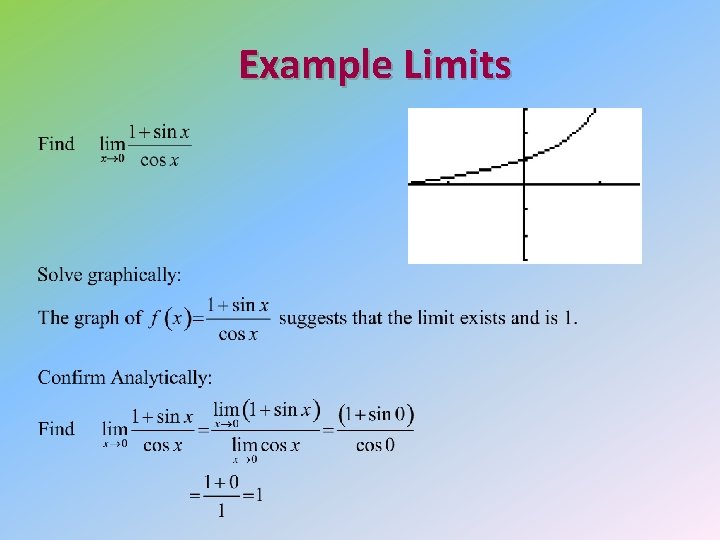
Example Limits

Example Limits

Example Limits [-6, 6] by [-10, 10]