Kapitel 4 Lernen als Optimierung SS 2009 Maschinelles

Kapitel 4: Lernen als Optimierung SS 2009 Maschinelles Lernen und Neural Computation 71

Lernen als Funktionsoptimierung • Gegeben: Fehlerfunktion (i. a. neg. log Likelihood) z. B. : • Gesucht: Gewichte (Parameter), die Funktion minimieren • Klassischer Fall von Funktionsoptimierung Optimierungstheorie SS 2009 Maschinelles Lernen und Neural Computation 72

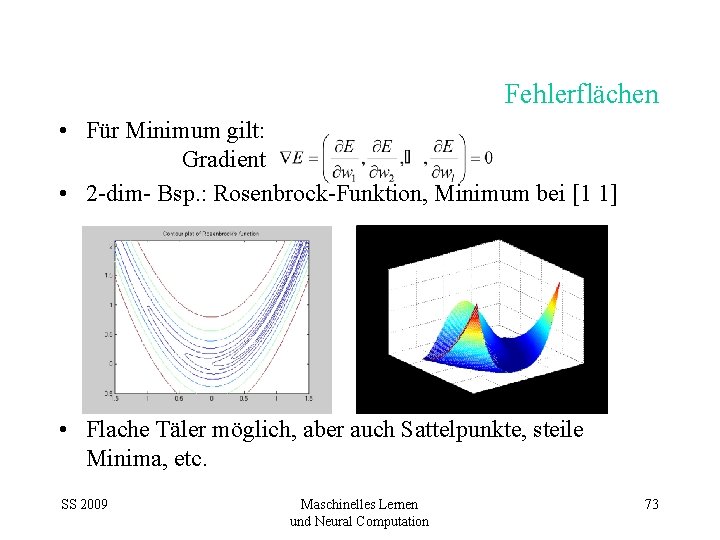
Fehlerflächen • Für Minimum gilt: Gradient • 2 -dim- Bsp. : Rosenbrock-Funktion, Minimum bei [1 1] • Flache Täler möglich, aber auch Sattelpunkte, steile Minima, etc. SS 2009 Maschinelles Lernen und Neural Computation 73

Gradient der Fehlerfunktion • Optimierung basiert auf Gradienteninformation: Beitrag der Fehlerfunktion Beitrag des Netzes • Backpropagation (nach Bishop 1995): effiziente Berechnung des Gradienten (Beitrag des Netzes): O(W) statt O(W 2), siehe p. 146 f • ist unabhängig von der gewählten Fehlerfunktion SS 2009 Maschinelles Lernen und Neural Computation 74

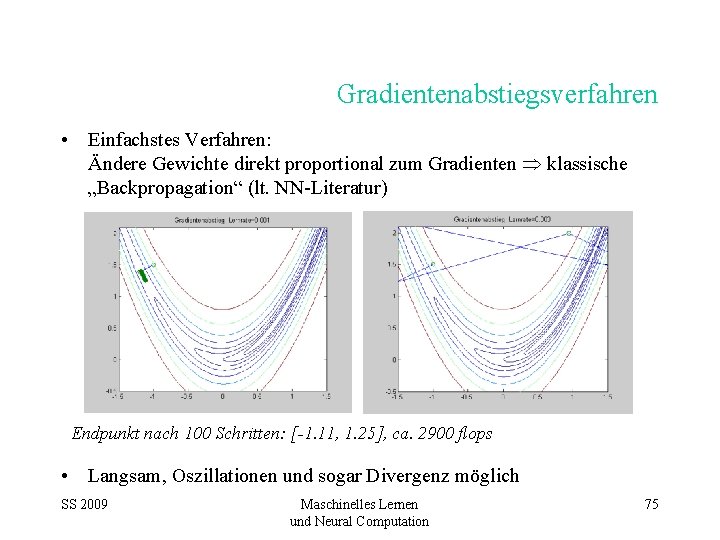
Gradientenabstiegsverfahren • Einfachstes Verfahren: Ändere Gewichte direkt proportional zum Gradienten klassische „Backpropagation“ (lt. NN-Literatur) Endpunkt nach 100 Schritten: [-1. 11, 1. 25], ca. 2900 flops • Langsam, Oszillationen und sogar Divergenz möglich SS 2009 Maschinelles Lernen und Neural Computation 75

Gradientenabstieg mit Momentum • Momentum=„Trägheit“ Endpunkt nach 100 Schritten: [0. 52, 0. 26]; ca. 3100 flops • Dämpft manche Oszillationen, erzeugt aber neue, • beschleunigt (vergleichbar mit rollender Kugel), • immer noch Divergenz möglich SS 2009 Maschinelles Lernen und Neural Computation 76

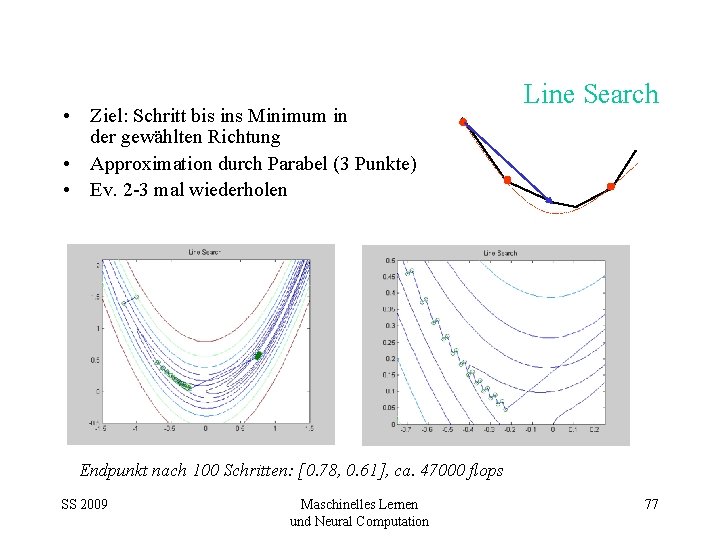
• Ziel: Schritt bis ins Minimum in der gewählten Richtung • Approximation durch Parabel (3 Punkte) • Ev. 2 -3 mal wiederholen Line Search Endpunkt nach 100 Schritten: [0. 78, 0. 61], ca. 47000 flops SS 2009 Maschinelles Lernen und Neural Computation 77

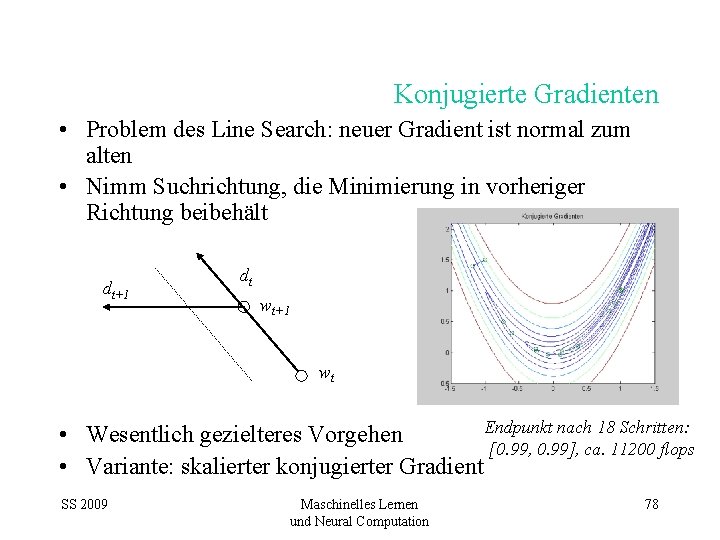
Konjugierte Gradienten • Problem des Line Search: neuer Gradient ist normal zum alten • Nimm Suchrichtung, die Minimierung in vorheriger Richtung beibehält dt+1 dt wt+1 wt Endpunkt nach 18 Schritten: • Wesentlich gezielteres Vorgehen [0. 99, 0. 99], ca. 11200 flops • Variante: skalierter konjugierter Gradient SS 2009 Maschinelles Lernen und Neural Computation 78

Quadratische Approximation • Annäherung der Fläche um einen beliebigen Punkt: Entspricht Paraboloid Hesse‘sche Matrix (alle 2. Ableitungen) • Annäherungsweise: • „Newton Richtung“, zeigt direkt Richtung Minimum (wenn Fläche quadratisch) • Newton Methode SS 2009 Maschinelles Lernen und Neural Computation 79

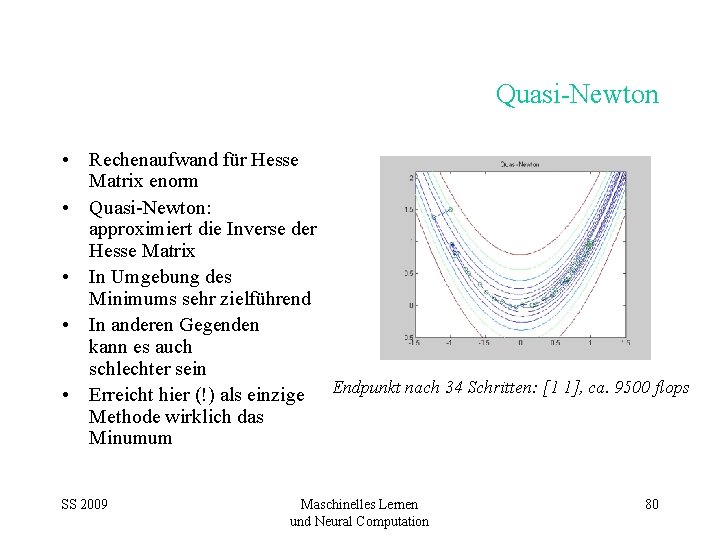
Quasi-Newton • Rechenaufwand für Hesse Matrix enorm • Quasi-Newton: approximiert die Inverse der Hesse Matrix • In Umgebung des Minimums sehr zielführend • In anderen Gegenden kann es auch schlechter sein • Erreicht hier (!) als einzige Endpunkt nach 34 Schritten: [1 1], ca. 9500 flops Methode wirklich das Minumum SS 2009 Maschinelles Lernen und Neural Computation 80

Mehrere Minima • Alle vorgestellten Verfahren sind lokale Optimierer • Globale Optimierer: Genetische Algorithmen, Stochastic Annealing • Es kann mehrere (lokale) Minima geben! • Verschiedene Minima können verschiedenen Teillösungen entsprechen • mehrere Durchläufe mit verschiedenen Initialisierungen • Aber: es gibt auch äquivalente Minima (durch Permutation der Hidden Units und Vertauschen der Vorzeichen): M!2 M äquivalente Minima (bei M H. U. ) SS 2009 Maschinelles Lernen und Neural Computation 81

Zusammenfassung • Gradientenbasierte Verfahren sind mächtige lokale Optimierer • Klassisches „Backpropagation“ (Gradientenabstieg) ist das schwächste davon • Aber: Backprop heißt effiziente Berechnung des Gradienten für neuronale Netze • Auch 2. Ableitung (Krümmung) nutzbar • Dringende Empfehlung: (skaliertes) konjugiertes Gradienten- oder Quasi-Newton-Verfahren verwenden! SS 2009 Maschinelles Lernen und Neural Computation 82