Investigating Identity and Inverse Matrices QUESTION What are

Investigating Identity and Inverse Matrices QUESTION: What are some properties of identity and inverse matrices? 1 1 Let A = 2 3 – 4 5 , B = – 7 identity matrix I = 1 0 0. 1 0. 8 6 , and C= 0. 6 0. 3. Consider the 2 2. Find AI, BI, and CI. What do you notice? 2 Find IA, IB, and IC using the matrices from Step 1. Is multiplication by the identity matrix commutative? 3 Let D = 4 Use matrix multiplication to decide which of the following is the inverse of the 7 4 5 3. The inverse of D is E = 3 – 4 matrix A in Step 1: 5 – 2 – 3 , 1 – 5 2 3 – 1 , or – 1 3 – 5. Find DE and ED. 7 2. – 5

Investigating Identity and Inverse Matrices DRAWING CONCLUSIONS For any 2 2 matrix A, what is true of the products AI and IA where I is the 2 2 identity matrix? Justify your answer mathematically. (Hint: Let A = a c b , and compute AI and IA. ) d 1 How is the relationship between I = 0 0 1 and other 2 2 matrices similar to the relationship between 1 and other real numbers? What do you think is the identity matrix for the set of 3 3 matrices? Check your answer by multiplying your proposed identity matrix by several 3 3 matrices.

Investigating Identity and Inverse Matrices DRAWING CONCLUSIONS What is the relationship between a matrix, its inverse, and the identity matrix? How is this relationship like the one that exists between a nonzero real number, its reciprocal, and 1? Does every nonzero matrix have an inverse? Explain. (Hint: Consider a 2 2 matrix whose first row contains all nonzero entries and whose second row contains all zero entries. ) Find the inverse of F = 2 1 7 4 a c b d = 2 1 7 4 by finding values of a, b, c, and d such that 1 0 0 1 .

Using Inverse Matrices The number 1 is a multiplicative identity for real numbers because 1 • a = a and a • 1 = a. For matrices, the n n identity matrix is the matrix that has 1’s on the main diagonal and 0’s elsewhere. 2 2 Identity Matrix I= 1 0 0 1 3 3 Identity Matrix I= 1 0 0 0 1 If A is any n n matrix and I is the n n identity matrix, then IA = A and AI = A. Two n n matrices are inverses of each other if their product (in both orders) is the n n identity matrix. For example, matrices A and B below are inverses of each other. 3 – 1 2 3 – 1 1 2 1 1 0 AB = = = I BA = = = I – 5 2 5 – 5 2 3 5 3 0 1 The symbol used for the inverse of A is A – 1.

Using Inverse Matrices The number 1 is a multiplicative identity for real numbers because 1 • a = a and a • 1 = a. For matrices, the n n identity matrix is the matrix that has 1’s on the main diagonal and 0’s elsewhere. THE INVERSE OF A 2 2 MATRIX The inverse of the matrix A = a c A – 1 = 1 | A| d –c –b a = b d 1 is d a d – c b –c –b a provided a d – c b 0.

Finding the Inverse of a 2 2 Matrix Find the inverse of A = 3 4 1. 2 SOLUTION A – 1 = CHECK 3 4 1 2 1 6– 4 2 – 4 – 1 1 = 3 2 2 – 4 – 1 = 3 1 1 2 – 2 3 2 You can check the inverse by showing that AA – 1 = I = A – 1 A. 1 – 2 1 2 3 2 = 1 0 0 1 1 1 2 – 2 3 2 and 3 4 1 1 = 2 0 0 1

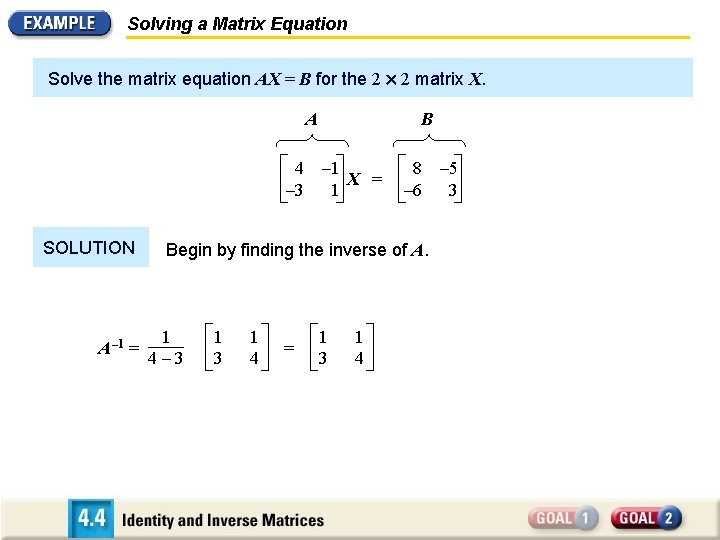
Solving a Matrix Equation Solve the matrix equation AX = B for the 2 2 matrix X. A 4 – 3 SOLUTION A – 1 = B – 1 X = 1 8 – 6 Begin by finding the inverse of A. 1 4– 3 1 4 = 1 3 1 4 – 5 3

Solving a Matrix Equation Solve the matrix equation AX = B for the 2 2 matrix X. A 4 – 3 B – 1 X = 1 8 – 6 – 5 3 To solve the equation for X, multiply both sides of the equation by A – 1 on the left. 1 3 1 4 4 – 3 – 1 X = 1 1 0 0 2 X = 1 0 – 2 – 3 IX = A – 1 B 2 0 – 2 – 3 X = A – 1 B X = 1 3 1 4 8 – 6 – 5 3 A – 1 AX = A – 1 B CHECK You can check the solution by multiplying A and X to see if you get B.

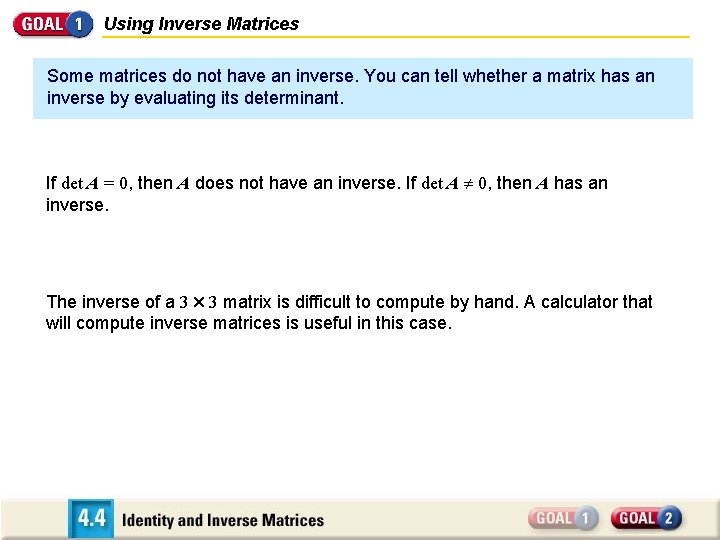
Using Inverse Matrices Some matrices do not have an inverse. You can tell whether a matrix has an inverse by evaluating its determinant. If det A = 0, then A does not have an inverse. If det A 0, then A has an inverse. The inverse of a 3 3 matrix is difficult to compute by hand. A calculator that will compute inverse matrices is useful in this case.

Using Inverse Matrices in Real Life A cryptogram is a message written according to a secret code. (The Greek word kruptos means hidden and the Greek word gramma means letter. ) The following technique uses matrices to encode and decode messages. First assign a number to each letter in the alphabet with 0 assigned to a blank space. _=0 E=5 J = 10 O = 15 T = 20 Y = 25 A=1 F=6 K = 11 P = 16 U = 21 Z = 26 B=2 G=7 L = 12 Q = 17 V = 22 C=3 H = 8 M = 13 D=4 I=9 N = 14 R = 18 W = 23 S = 19 X = 24 Then convert the message to numbers partitioned into 1 2 uncoded row matrices. To encode a message, choose a 2 2 matrix A that has an inverse and multiply the uncoded row matrices by A on the right to obtain coded row matrices.

Converting a Message Use the list below to convert the message GET HELP to row matrices. SOLUTION _=0 E=5 J = 10 O = 15 T = 20 Y = 25 A=1 F=6 K = 11 P = 16 U = 21 Z = 26 B=2 G=7 L = 12 Q = 17 V = 22 C=3 H=8 M = 13 R = 18 W = 23 D=4 I=9 N = 14 S = 19 X = 24 G E T _ H E L P [7 5] [20 0] [8 5] [12 16]

Encoding a Message CRYPTOGRAPHY Use A = 2 – 1 3 to encode the message GET HELP. – 2 SOLUTION The coded row matrices are obtained by multiplying each of the uncoded row matrices from the previous example by the matrix A on the right. UNCODED ROW MATRIX ENCODING MATRIX A CODED ROW MATRIX [7 5] 2 – 1 3 – 2 = [9 11] [20 0] 2 – 1 3 – 2 = [40 60] [8 5] 2 – 1 3 – 2 = [11 14] [12 16] 2 – 1 3 – 2 = [8 4] The coded message is 9, 11, 40, 60, 11, 14, 8, 4.

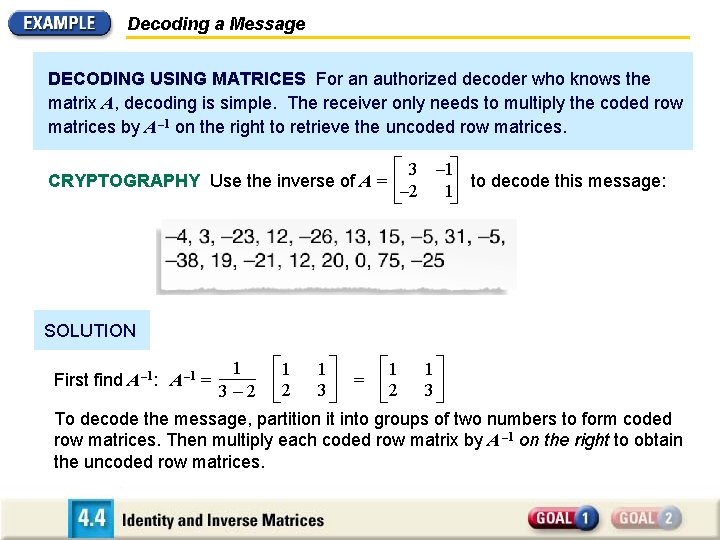
Decoding a Message DECODING USING MATRICES For an authorized decoder who knows the matrix A, decoding is simple. The receiver only needs to multiply the coded row matrices by A – 1 on the right to retrieve the uncoded row matrices. 3 – 2 CRYPTOGRAPHY Use the inverse of A = – 1 to decode this message: 1 SOLUTION First find A – 1: A – 1 = 1 3– 2 1 3 = 1 2 1 3 To decode the message, partition it into groups of two numbers to form coded row matrices. Then multiply each coded row matrix by A – 1 on the right to obtain the uncoded row matrices.

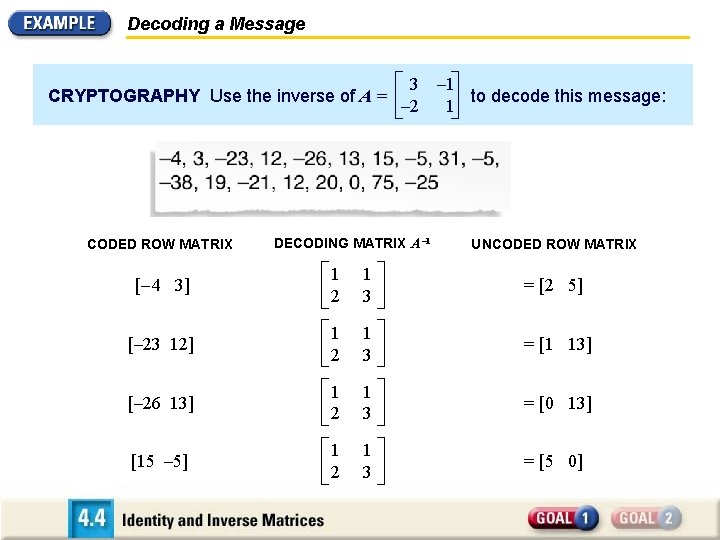
Decoding a Message CRYPTOGRAPHY Use the inverse of A = CODED ROW MATRIX 3 – 2 DECODING MATRIX A – 1 to decode this message: 1 UNCODED ROW MATRIX [– 4 3] 1 2 1 3 = [2 5] [– 23 12] 1 2 1 3 = [1 13] [– 26 13] 1 2 1 3 = [0 13] [15 – 5] 1 2 1 3 = [5 0]

Decoding a Message CRYPTOGRAPHY Use the inverse of A = CODED ROW MATRIX 3 – 2 DECODING MATRIX A – 1 to decode this message: 1 UNCODED ROW MATRIX [31 – 5] 1 2 1 3 = [21 16] [– 38 19] 1 2 1 3 = [0 19] [– 21 12] 1 2 1 3 = [3 15] [20 1 2 1 3 = [20 20] 0]

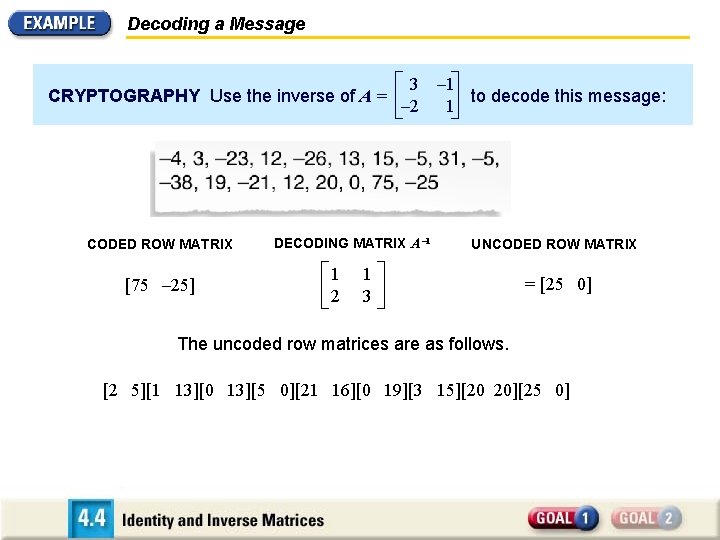
Decoding a Message CRYPTOGRAPHY Use the inverse of A = CODED ROW MATRIX [75 – 25] 3 – 2 DECODING MATRIX A – 1 1 2 – 1 to decode this message: 1 UNCODED ROW MATRIX 1 3 = [25 0] The uncoded row matrices are as follows. [2 5][1 13][0 13][5 0][21 16][0 19][3 15][20 20][25 0]

Decoding a Message CRYPTOGRAPHY Use the inverse of A = 3 – 2 – 1 to decode this message: 1 _=0 E=5 J = 10 O = 15 T = 20 Y = 25 A=1 F=6 K = 11 P = 16 U = 21 Z = 26 B=2 G=7 L = 12 Q = 17 V = 22 C=3 H = 8 M = 13 D=4 I=9 N = 14 R = 18 W = 23 S = 19 X = 24 You can read the message as follows: [2 5][1 13][0 13][5 0][21 16][0 19][3 15][20 20][25 0] B E A M _ M E _ U P _ S C O T T Y _