Internal Order and Symmetry GLY 4200 Fall 2019














- Slides: 23

Internal Order and Symmetry GLY 4200 Fall, 2019 © D. L. Warburton 2019 1

Symmetry • The simple symmetry operations not involving displacement are: § Rotation § Reflection § Inversion 2

Symmetry Elements • Each symmetry operation has an associated symmetry element § Rotation about an axis (A 2, A 3, A 4, or A 6 – in combination we use 2, 3, 4 or 6) § Reflection across a mirror plane § Inversion through a point, the center of symmetry 3

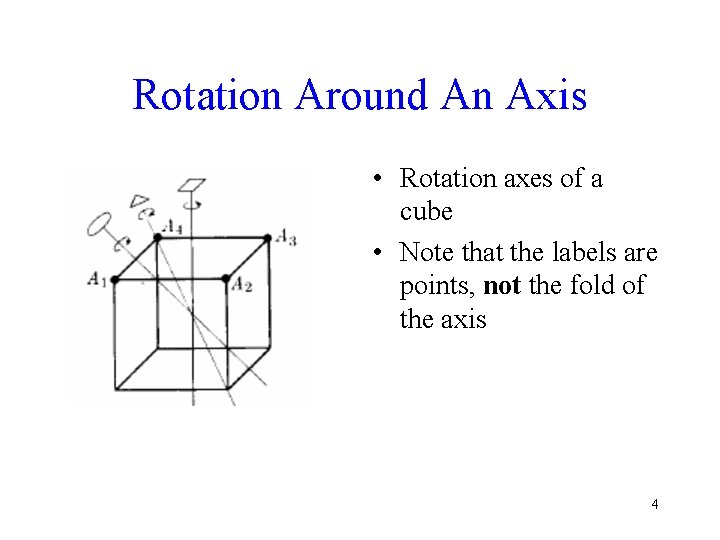
Rotation Around An Axis • Rotation axes of a cube • Note that the labels are points, not the fold of the axis 4

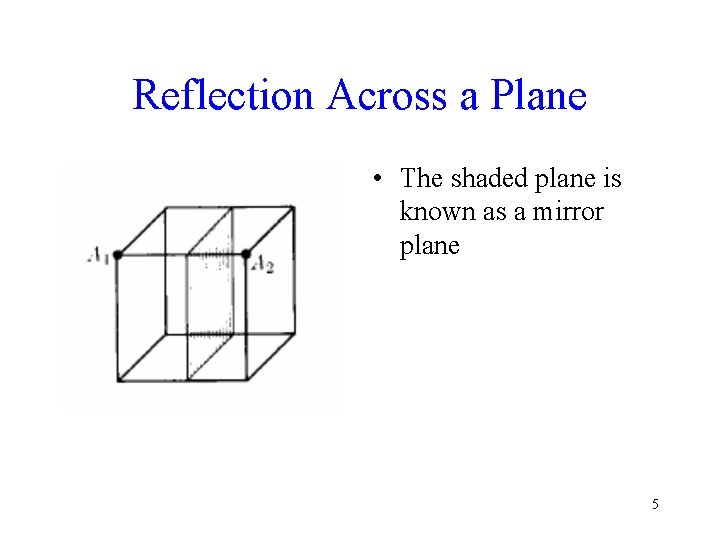
Reflection Across a Plane • The shaded plane is known as a mirror plane 5

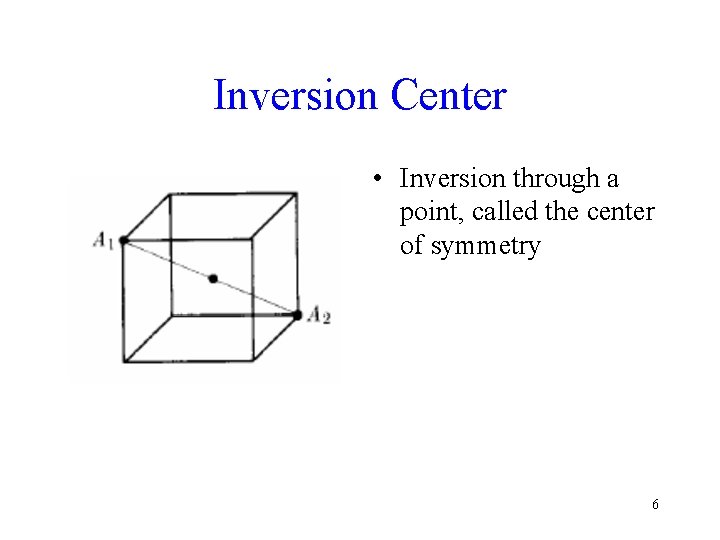
Inversion Center • Inversion through a point, called the center of symmetry 6

Symmetry Operation • Any action which, when performed on an object, leaves the object in a manner indistinguishable from the original object • Example – sphere § Any action performed on a sphere leaves the sphere in a manner identical to the original § A sphere thus has the highest possible symmetry 7

Identity Operation • All groups must have an identity operation • We choose an A 1 rotation as the identity operation • A 1 involves rotation by 360º/n, where n is the fold of the axis • Therefore A 1 = 360º/1 = 360º 8

Combinations of Simple Operations • We may combine our simple symbols in certain ways • 2/m means a two-fold rotation with a mirror plane perpendicular to it • Similarly 4/m and 6/m 9

Parallel Mirror Planes • 2 mm 2 fold with two parallel mirror planes • 3 m 3 fold with 3 parallel mirror planes • 4 mm 4 fold with 2 sets of parallel mirror planes • 6 mm 6 fold with 2 sets of parallel mirror planes 10

Special Three Fold Axis • 3/m 3 fold with a perpendicular mirror plane • Equivalent to a 6 fold rotation inversion 11

2/m 2/m • May be written 2/mmm • Three 2 -fold axes, mutually perpendicular, with a mirror plane perpendicular to each 12

4/m 2/m • A four fold axis has a mirror plane perpendicular to it • There is a two-fold axis, with a ⊥ mirror plane, ⊥ to the four-fold axis – the A 4 duplicate the A 2 90º away • There is a second set of two-fold axes, with ⊥ mirror planes, ⊥ to the four-fold axis – the A 4 duplicate the A 2’s 90º away 13

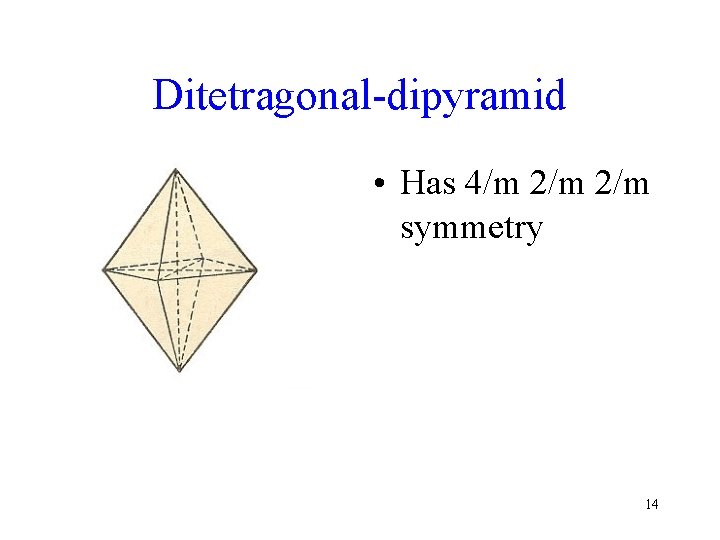
Ditetragonal-dipyramid • Has 4/m 2/m symmetry 14

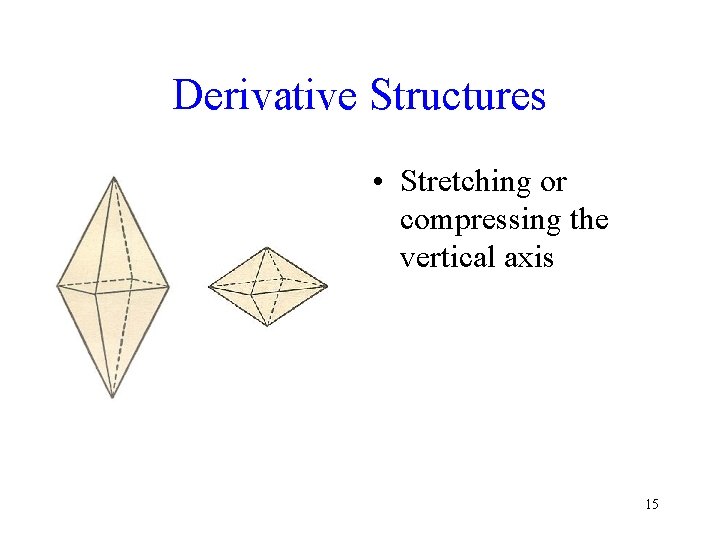
Derivative Structures • Stretching or compressing the vertical axis 15

Hermann – Mauguin symbols • The symbols we have been demonstrating are called Hermann – Mauguin (H-M) symbols • There are other systems in use, but the H-M symbols are used in mineralogy, and are easy to understand than some of the competing systems 16

Complex Symmetry Operations • The operations defined thus far are simple operations • Complex operations involve a combination of two simple operations • Two possibilities are commonly used § Roto-inversion § Roto-reflection • It is not necessary that either operation exist separately 17

Roto-Inversion • This operation involves rotation through a specified angle around a specified axis, followed by inversion through the center of symmetry • The operations are denoted bar 1, bar 2, bar 3, bar 4, or bar 6 18

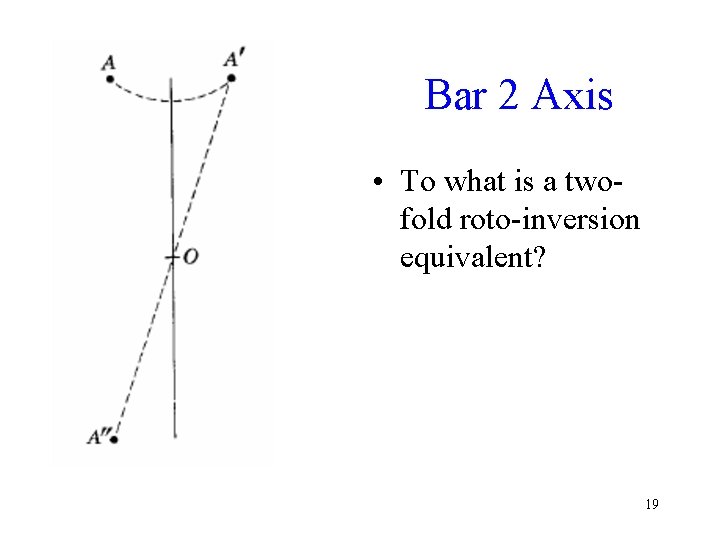
Bar 2 Axis • To what is a twofold roto-inversion equivalent? 19

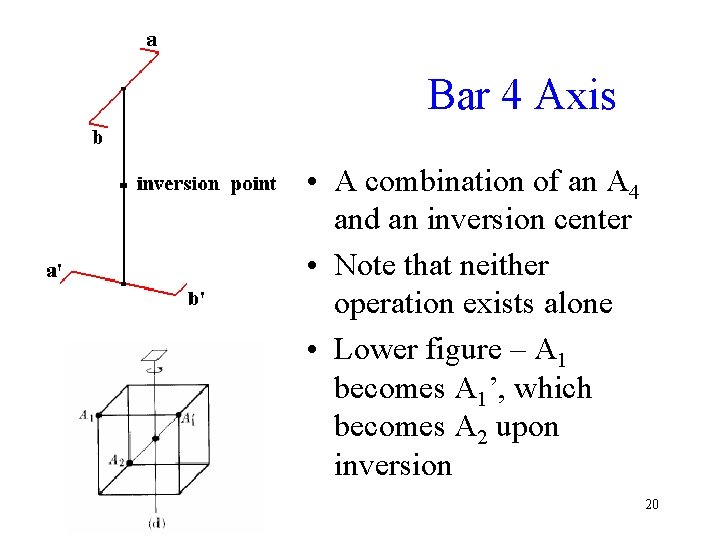
Bar 4 Axis • A combination of an A 4 and an inversion center • Note that neither operation exists alone • Lower figure – A 1 becomes A 1’, which becomes A 2 upon inversion 20

Hexagonal Scalenohedron • This was model #11 in the plastic set • The vertical axis is a bar. A 3, not an A 6 • Known as a scalenohedron because each face is a scalene triangle • The horizontal red axes are A 2 • There are mp’s to the A 2 axes • The H-M symbol is bar 3 2/m 21

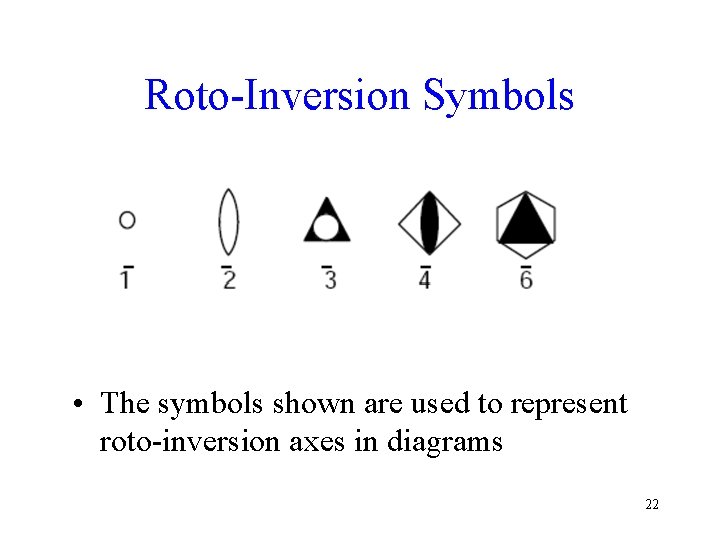
Roto-Inversion Symbols • The symbols shown are used to represent roto-inversion axes in diagrams 22

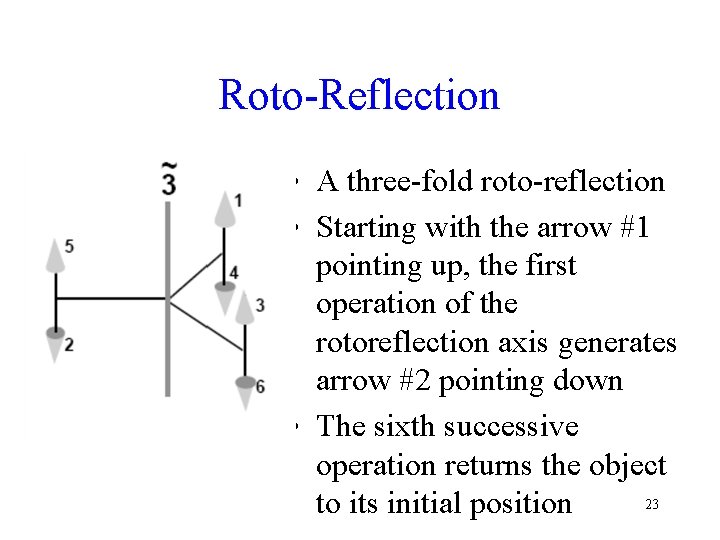
Roto-Reflection • A three-fold roto-reflection • Starting with the arrow #1 pointing up, the first operation of the rotoreflection axis generates arrow #2 pointing down • The sixth successive operation returns the object 23 to its initial position
![Complexes of the type [m(aa)3]tn Complexes of the type [m(aa)3]tn](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20200%20200%22%3E%3C/svg%3E) Complexes of the type [m(aa)3]tn
Complexes of the type [m(aa)3]tn Gly
Gly Gly
Gly 9300 to 34800
9300 to 34800 Srx 4200
Srx 4200 Issai standards
Issai standards 61000x12
61000x12 Audit and compliance principles
Audit and compliance principles Via optica
Via optica Symmetry powerpoint presentation
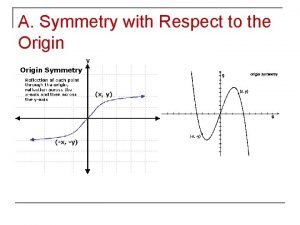
Symmetry powerpoint presentation What is origin symmetry
What is origin symmetry Dm 31 s 2019
Dm 31 s 2019 Internal control introduction
Internal control introduction Vouching in auditing
Vouching in auditing Rotations on the coordinate plane
Rotations on the coordinate plane Isosceles trapezium order of rotational symmetry
Isosceles trapezium order of rotational symmetry What is the order of rotational symmetry of a manx cross
What is the order of rotational symmetry of a manx cross Tom suk
Tom suk Answer
Answer Altaeast
Altaeast Natural order sentence example
Natural order sentence example Antagonistic effect
Antagonistic effect First order drug elimination
First order drug elimination Second order change
Second order change
![Complexes of the type [m(aa)3]tn Complexes of the type [m(aa)3]tn](https://slidetodoc.com/wp-content/uploads/2020/12/3015715_d8412bc28f0c7b6a8c2ea3744ce60d97-300x225.jpg)