Initiation la programmation imprative et algorithmique Cours 7

Initiation à la programmation impérative et algorithmique Cours 7 – Récursivité Largement inspiré des cours : Vercouter, Del Mondo & Delestre, Hérault, Mainguenaud (INSA de Rouen) Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Définition et exemples Une entité est récursive lorsqu’on l’utilise pour la définir. Factorielle 0! = 1 n! = n(n - 1)! Suite de fibonacci F(0) = 0 F(1) = 1 F(n) = F(n – 1) + F(n – 2), n>1 Poupée russe Une poupée russe est : • une poupée « pleine » • une poupée vide contenant une poupée russe Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Exemple de pseudo-code Ø Factorielle fonction fact (n : Naturel) : Naturel debut si (n=0) OU (n=1) alors retourner 1 sinon retourner n*fact(n-1) finsi fin Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Récursivité terminale On parle de récursivité terminale lorsque l’appel récursif est la dernière instruction de la fonction et qu’elle est isolée. fonction plus(a, b : Entier) : Entier debut si b=0 alors retourner a sinon retourner plus(a+1, b-1) finsi fin => plus(4, 2)=plus(5, 1)=plus(6, 0)=6 Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Récursivité non terminale On parle de récursivité non terminale lorsque l’appel récursif n’est pas la dernière instruction de la fonction et/ou qu’elle n’est pas isolée (fait partie d’une expression). fonction plus(a, b : Entier) : Entier debut si b=0 alors retourner a sinon retourner 1+plus(a, b-1) finsi fin => plus(4, 2)=1+plus(4, 1)=1+1+plus(4, 0)=6 Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Méthode Pour écrire un algorithme récursif, il faut analyser le problème et identifier : • Le ou les cas particuliers, par ex. qui initient la récursion • Le cas général qui effectue la récursion Lorsqu’on écrit un algorithme récursif, au moment de l’appel récursif, on se place en tant qu’utilisateur de l’algorithme : on considère donc que le problème est résolu Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

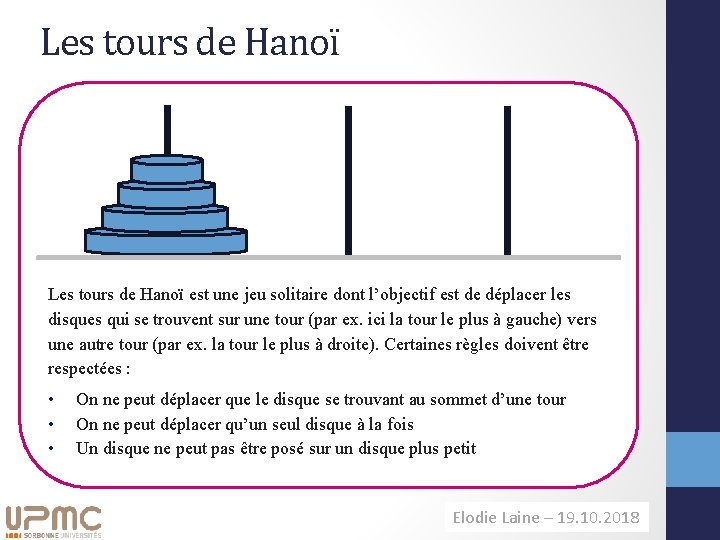
Les tours de Hanoï est une jeu solitaire dont l’objectif est de déplacer les disques qui se trouvent sur une tour (par ex. ici la tour le plus à gauche) vers une autre tour (par ex. la tour le plus à droite). Certaines règles doivent être respectées : • • • On ne peut déplacer que le disque se trouvant au sommet d’une tour On ne peut déplacer qu’un seul disque à la fois Un disque ne peut pas être posé sur un disque plus petit Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

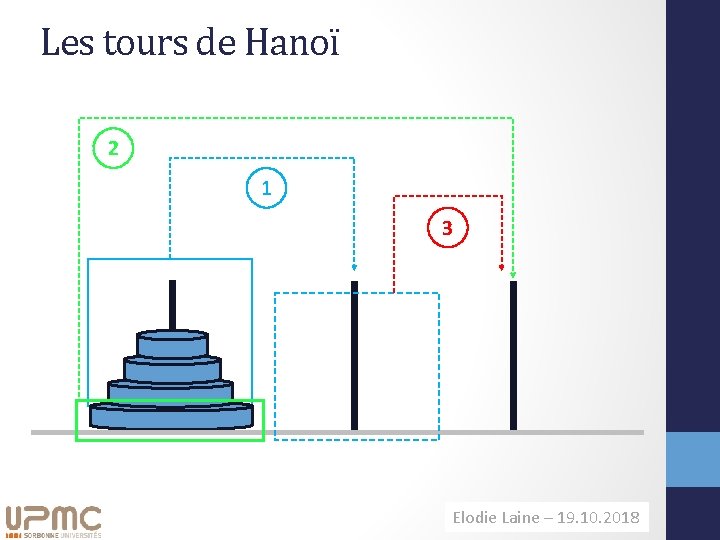
Les tours de Hanoï 2 1 3 Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Les tours de Hanoï Type défini dans le programme Opérations disponibles Pour résoudre le problème des tours de Hanoï, on dispose des fonctions suivantes : • fonction depiler. Tour (t : Tour. De. Hanoi, d : Disque) Cette fonction permet d’extraire un disque d d’une tour de Hanoï t • fonction empiler. Tour (t : Tour. De. Hanoi, d : Disque) Cette fonction permet de poser un disque d sur une tour de Hanoï t Objectif L’objectif consiste à écrire une fonction récursive visant à résoudre le problème des tours de Hanoï : fonction resoudre. Tours. De. Hanoi (nb. Disques. ADeplacer : Entier, source, destination, intermediaire : Tour. De. Hanoi) Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Les tours de Hanoï fonction resoudre. Tours. De. Hanoi (nb. Disques. ADeplacer : Entier, source, destination, intermediaire : Tour. De. Hanoi) Declaration d : Disque debut si nb. Disques. ADeplacer > 0 alors resoudre. Tour. De. Hanoi(nb. Disques. ADeplacer-1, source, intermediaire, destination) depiler(source, d) empiler(destination, d) resoudre. Tour. De. Hanoi(nb. Disques. ADeplacer-1, intermediaire, destination, source) finsi fin Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Tris récursifs Objectif L’objectif consiste à écrire une fonction récursive visant à trier des valeurs dans un tableau : fonction trier(t : Tableau[1. . MAX] d’Elements, nb. Elements : Entier) Tris non récursifs La compléxité des tris non récursifs vus jusqu’à présent est quadratique : • Tri à bulles (O(n 2)) • Tri par sélection (O(n 2)) • Tri par insertion (O(n 2)) Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Tris récursifs Principe L’algorithme des tris récursifs est basé sur le principe suivant : • • • Diviser : Le tableau à trier est divisé en deux Régner : Les deux sous-tableaux sont triés indépendemment Combiner : Les deux tableaux sont combinés Plus particulièrement, le tri rapide (ou quick-sort) repose sur une stratégie efficace de division du tableau (partitionnement). Il se déroule comme suit : 1/ Partitionnement du tableau autour d’un élément pivot de sorte que tous les éléments du sous-tableau gauche sont plus petits que le pivot 2/ Tri des sous-tableaux gauche et droit de la même façon Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Le tri rapide (quick sort) fonction tri. Rapide(t : Tableau[1. . MAX] d’Entier, nb : Entier) debut tri. Rapide. Recursif(t, 1, nb) fin fonction tri. Rapide. Recursif (t : Tableau[1. . MAX] d’Entier, d, f : Entier) Declaration indice. Pivot : Entier debut si d < f alors partitionner(t, d, f, indice. Pivot) tri. Rapide. Recursif(t, d, indice. Pivot – 1) tri. Rapide. Recursif(t, indice. Pivot + 1, f) finsi fin Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

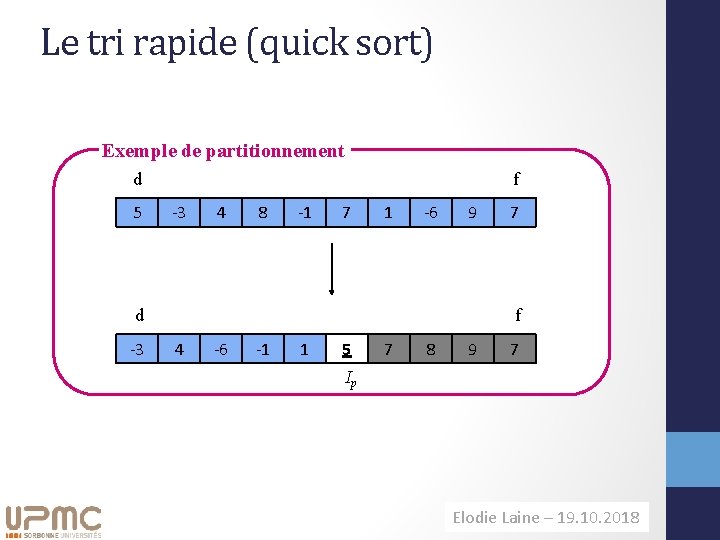
Le tri rapide (quick sort) Exemple de partitionnement d 5 f -3 4 8 -1 7 1 -6 9 d -3 7 f 4 -6 -1 1 5 7 8 9 7 Ip Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

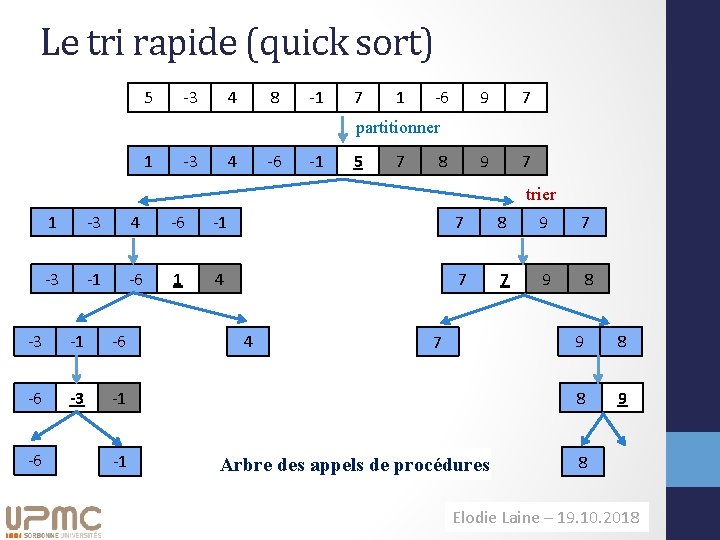
Le tri rapide (quick sort) 5 -3 4 8 -1 7 1 -6 9 7 partitionner 1 -3 4 -6 -1 5 7 8 trier 1 -3 4 -6 -1 7 8 9 7 -3 -1 -6 1 4 7 7 9 8 -3 -1 -6 -6 -3 -1 -6 -1 4 7 Arbre des appels de procédures 9 8 8 9 8 Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

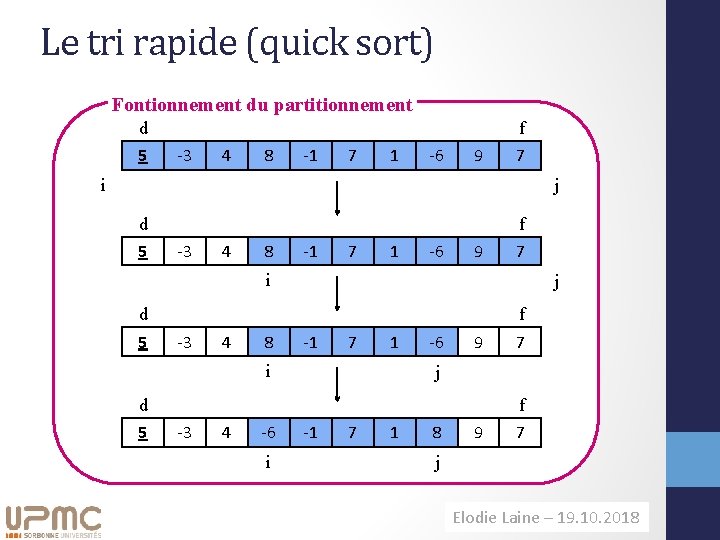
Le tri rapide (quick sort) Fontionnement du partitionnement d 5 f -3 4 8 -1 7 1 -6 9 7 i j d 5 f -3 4 8 -1 7 1 i -6 9 j d 5 7 f -3 4 -6 i -1 7 1 8 9 7 j Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

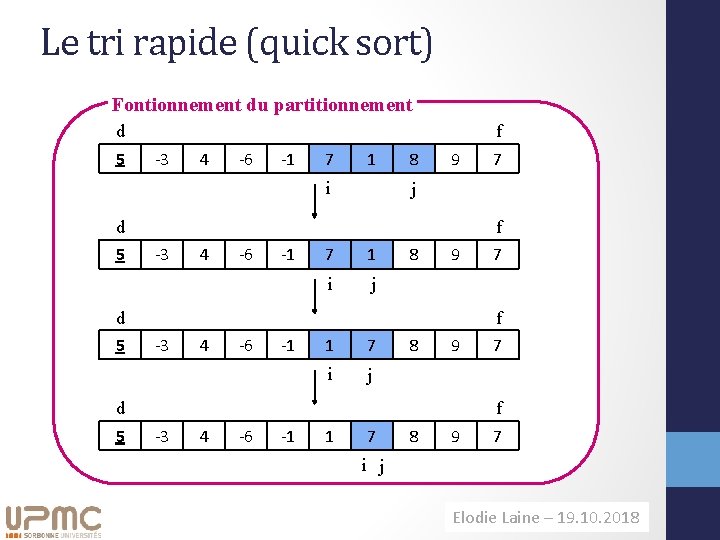
Le tri rapide (quick sort) Fontionnement du partitionnement d 5 f -3 4 -6 -1 7 1 i 8 9 j d 5 f -3 4 -6 -1 7 1 i j 8 9 d 5 7 f -3 4 -6 -1 1 7 i j 8 9 d 5 7 7 f -3 4 -6 -1 1 7 8 9 7 i j Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

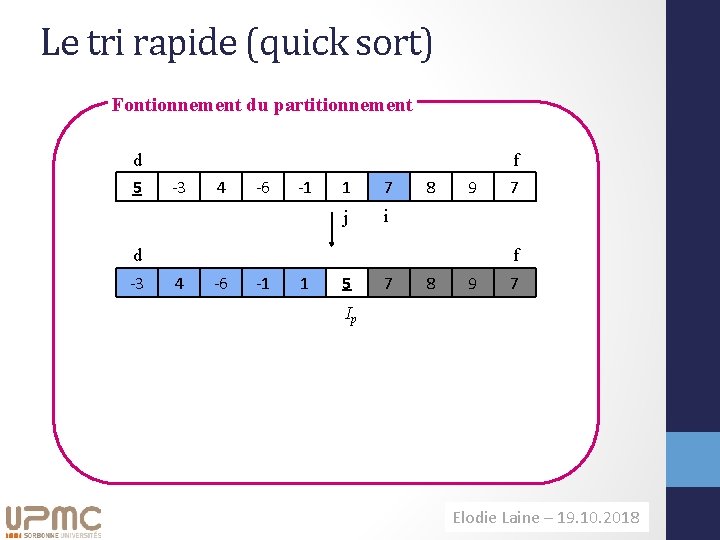
Le tri rapide (quick sort) Fontionnement du partitionnement d 5 f -3 4 -6 -1 1 7 j i 8 9 d -3 7 f 4 -6 -1 1 5 7 8 9 7 Ip Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Le tri rapide (quick sort) fonction partitionner(t : Tableau[1. . MAX] d’Entier, debut, fin : Entier) Declaration i, j, pivot, indice. Pivot : Entier debut pivot ← t[debut] i ← debut j ← fin tant que i ≤ j faire tant que t[i] ≤ pivot et i ≤ j faire i←i+1 fintantque tant que t[j] ≥ pivot et i ≤ j faire j←j– 1 fintantque si i ≤ j alors echanger(t[i], t[j]) finsi fintantque indice. Pivot ← j echanger(t[debut], t[j]) fin Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Le tri rapide (quick sort) fonction partitionner(t : Tableau[1. . MAX] d’Entier, debut, fin : Entier) Declaration i, j, pivot, indice. Pivot : Entier debut pivot ← t[debut] i ← debut j ← fin tant que i ≤ j faire si t[i] ≤ pivot alors i←i+1 sinon si t[j] ≥ pivot alors j←j– 1 sinon echanger(t[i], t[j]) finsi fintantque indice. Pivot ← j echanger(t[debut], t[j]) fin Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Le tri rapide (quick sort) Calcul de la complexité La fonction de partitionnement a une complexite en n. La complexité du tri rapide dépend dont du nombre d’appels récursifs (hauteur h de l’arbre de récursion) • • • Dans le meilleur des cas, le partitionnement coupe le tableau en deux parties de même longueur (à plus ou moins 1 près) On a : n = 2 h, donc h = log 2 n Donc on a Ω(nlog 2 n) Dans le pire des cas, le partitionnement coupe le tableau en deux sous tableaux, l’un de longeur 1 et l’autre n – 1 Dans ce cas h = n Et donc on a O(n 2) En moyenne on a θ(nlog 2 n) Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard

Conclusion • Les algorithmes récursifs sont simples et permettent de résoudre des problèmes complexes. • Il existe deux types de récursivité : • terminale, qui algorithmiquement peut être transformée en nonrécursivité • non terminale • Les algorithmes récursifs sont le plus souvent plus gourmands en ressource que leurs équivalents non récursifs. • Il existe plusieurs algorithmes de tri que le peut classer selon la méthode utilisée (itératifs ou récursifs) et leur performance • D’autres méthodes de tri existent, qui ne sont pas présentées dans ce cours : le tri par fusion, le shellsort, le tri par tas (ou heapsort), le radixsort. . etc. Elodie Laine– – 11. 09. 2014 19. 10. 2018 H. Richard