Information Retrieval Models Probabilistic Models Cheng Xiang Zhai

Information Retrieval Models: Probabilistic Models Cheng. Xiang Zhai Department of Computer Science University of Illinois, Urbana-Champaign

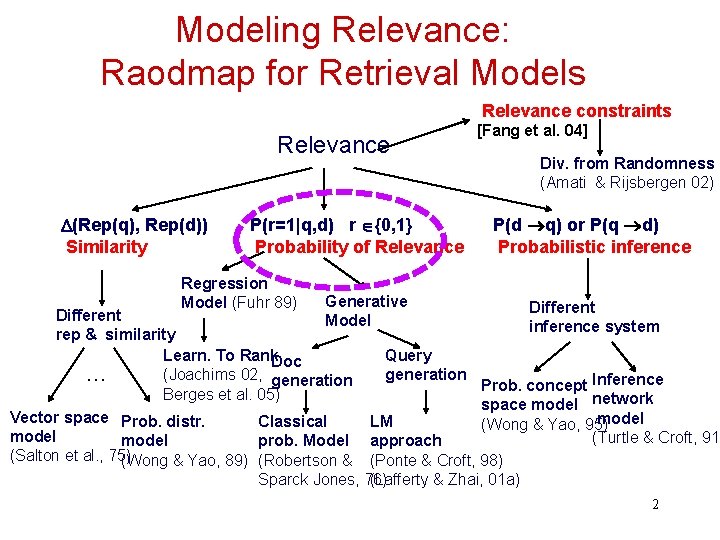
Modeling Relevance: Raodmap for Retrieval Models Relevance constraints Relevance (Rep(q), Rep(d)) Similarity P(r=1|q, d) r {0, 1} Probability of Relevance Regression Model (Fuhr 89) [Fang et al. 04] Div. from Randomness (Amati & Rijsbergen 02) P(d q) or P(q d) Probabilistic inference Generative Model Different inference system rep & similarity Learn. To Rank. Doc Query (Joachims 02, generation … Prob. concept Inference Berges et al. 05) space model network Vector space Prob. distr. model Classical LM (Wong & Yao, 95) model (Turtle & Croft, 91) model prob. Model approach (Salton et al. , 75) (Wong & Yao, 89) (Robertson & (Ponte & Croft, 98) Sparck Jones, 76) (Lafferty & Zhai, 01 a) 2

The Basic Question What is the probability that THIS document is relevant to THIS query? Formally… 3 random variables: query Q, document D, relevance R {0, 1} Given a particular query q, a particular document d, p(R=1|Q=q, D=d)=?

Probability of Relevance • Three random variables – Query Q – Document D – Relevance R {0, 1} • Goal: rank D based on P(R=1|Q, D) – Evaluate P(R=1|Q, D) – Actually, only need to compare P(R=1|Q, D 1) with P(R=1|Q, D 2), I. e. , rank documents • Several different ways to refine P(R=1|Q, D) 4

Probabilistic Retrieval Models: Intuitions Suppose we have a large number of relevance judgments (e. g. , clickthroughs: “ 1”=clicked; “ 0”= skipped) We can score documents based on Query(Q) Doc (D) Rel (R) ? Q 1 D 1 1 Q 1 D 2 1 Q 1 D 3 0 Q 1 D 4 0 Q 1 D 5 1 … Q 1 D 1 0 Q 1 D 2 1 Q 1 D 3 0 Q 2 D 3 1 Q 3 D 1 1 Q 4 D 2 1 Q 4 D 3 0 … P(R=1|Q 1, D 1)=1/2 P(R=1|Q 1, D 2)=2/2 P(R=1|Q 1, D 3)=0/2 … What if we don’t have (sufficient) search log? We can approximate p(R=1|Q, D)! Different assumptions lead to different models 5

Refining P(R=1|Q, D): Generative models • Basic idea – Define P(Q, D|R) – Compute O(R=1|Q, D) using Bayes’ rule Ignored for ranking D • Special cases – Document “generation”: P(Q, D|R)=P(D|Q, R)P(Q|R) – Query “generation”: P(Q, D|R)=P(Q|D, R)P(D|R) 6

Document Generation Model of relevant docs for Q Model of non-relevant docs for Q Assume independent attributes A 1…Ak …. (why? ) Let D=d 1…dk, where dk {0, 1} is the value of attribute Ak (Similarly Q=q 1…qk ) 7

Robertson-Sparck Jones Model (Robertson & Sparck Jones 76) (RSJ model) Two parameters for each term Ai: pi = P(Ai=1|Q, R=1): prob. that term Ai occurs in a relevant doc qi = P(Ai=1|Q, R=0): prob. that term Ai occurs in a non-relevant doc How to estimate parameters? Suppose we have relevance judgments, “+0. 5” and “+1” can be justified by Bayesian estimation 8

RSJ Model: No Relevance Info (Croft & Harper 79) (RSJ model) How to estimate parameters? Suppose we do not have relevance judgments, - We will assume pi to be a constant - Estimate qi by assuming all documents to be non-releva N: # documents in collection ni: # documents in which term Ai occurs 9

RSJ Model: Summary • The most important classic prob. IR model • Use only term presence/absence, thus also referred to as Binary Independence Model • Essentially Naïve Bayes for doc ranking • Most natural for relevance/pseudo feedback • When without relevance judgments, the model parameters must be estimated in an ad hoc way • Performance isn’t as good as tuned VS model 10

Improving RSJ: Adding TF Basic doc. generation model: Let D=d 1…dk, where dk is the frequency count of term Ak 2 -Poisson mixture model Many more parameters to estimate! (how many exactly? ) 11

BM 25/Okapi Approximation (Robertson et al. 94) • Idea: Approximate p(R=1|Q, D) with a simpler function that share similar properties • Observations: – log O(R=1|Q, D) is a sum of term weights Wi – Wi= 0, if TFi=0 – Wi increases monotonically with Tfi – Wi has an asymptotic limit • The simple function is 12

Adding Doc. Length & Query TF • Incorporating doc length – Motivation: The 2 -Poisson model assumes equal document length – Implementation: “Carefully” penalize long doc • Incorporating query TF – Motivation: Appears to be not well-justified – Implementation: A similar TF transformation • The final formula is called BM 25, achieving top TREC performance 13

The BM 25 Formula “Okapi TF/BM 25 TF” 14

Extensions of “Doc Generation” Models • Capture term dependence (Rijsbergen & Harper 78) • Alternative ways to incorporate TF (Croft 83, Kalt 96) • Feature/term selection for feedback (Okapi’s TREC reports) • Estimate of the relevance model based on pseudo feedback, to be covered later [Lavrenko & Croft 01] 15

What You Should Know • Basic idea of probabilistic retrieval models • How to use Bayes Rule to derive a general document-generation retrieval model • How to derive the RSJ retrieval model (i. e. , binary independence model) • Assumptions that have to be made in order to derive the RSJ model • The two-Poisson model and the heuristics introduced to derive BM 25 16