Formal Retrieval Frameworks Cheng Xiang Zhai Department of

Formal Retrieval Frameworks Cheng. Xiang Zhai (翟成祥) Department of Computer Science Graduate School of Library & Information Science Institute for Genomic Biology, Statistics University of Illinois, Urbana-Champaign http: //www-faculty. cs. uiuc. edu/~czhai, czhai@cs. uiuc. edu 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 1

Outline • Risk Minimization Framework [Lafferty & Zhai 01, Zhai & Lafferty 06] • Axiomatic Retrieval Framework [Fang et al. 04, Fang & Zhai 05, Fang & Zhai 06] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 2

Risk Minimization Framework 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 3

Risk Minimization: Motivation • Long-standing IR Challenges – Improve IR theory • Develop theoretically sound and empirically effective models • Go beyond the limited traditional notion of relevance (independent, topical relevance) – Improve IR practice • Optimize retrieval parameters automatically • SLMs are very promising tools … – How can we systematically exploit SLMs in IR? – Can SLMs offer anything hard/impossible to achieve in traditional IR? 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 4

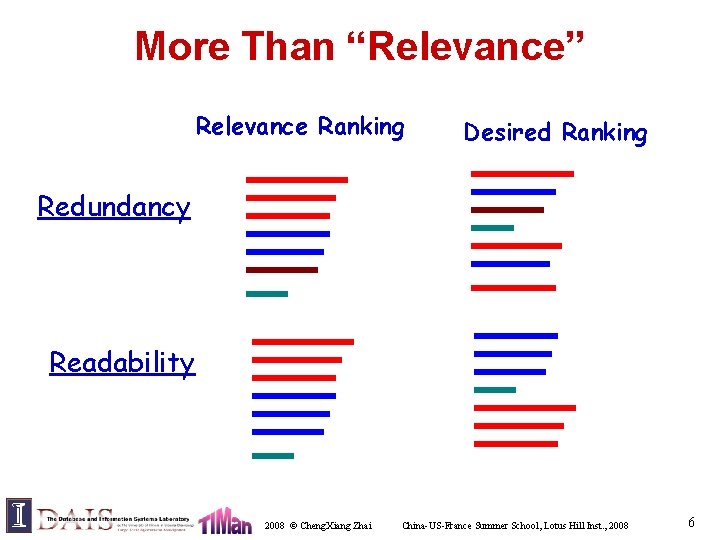
Long-Standing IR Challenges • Limitations of traditional IR models – Strong assumptions on “relevance” • Independent relevance • Topical relevance – Can we go beyond this traditional notion of relevance? • Difficulty in IR practice – Ad hoc parameter tuning – Can’t go beyond “retrieval” to support info. access in general 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 5

More Than “Relevance” Relevance Ranking Desired Ranking Redundancy Readability 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 6

Retrieval Parameters • Retrieval parameters are needed to – model different user preferences – customize a retrieval model according to different queries and documents • So far, parameters have been set through empirical experimentation • Can we set parameters automatically? 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 7

Systematic Applications of Language Models to IR • Many different variants of language models have been developed, but are there many more models to be studied? • Can we establish a road map for exploring language models in IR? 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 8

Two Main Ideas of the Risk Minimization Framework • Retrieval as a decision process • Systematic language modeling 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 9

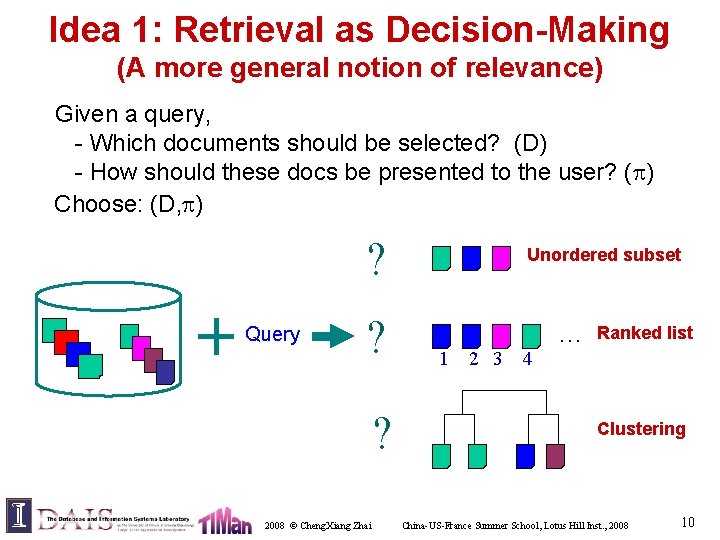
Idea 1: Retrieval as Decision-Making (A more general notion of relevance) Given a query, - Which documents should be selected? (D) - How should these docs be presented to the user? ( ) Choose: (D, ) ? Query ? ? 2008 © Cheng. Xiang Zhai Unordered subset 1 2 3 4 … Ranked list Clustering China-US-France Summer School, Lotus Hill Inst. , 2008 10

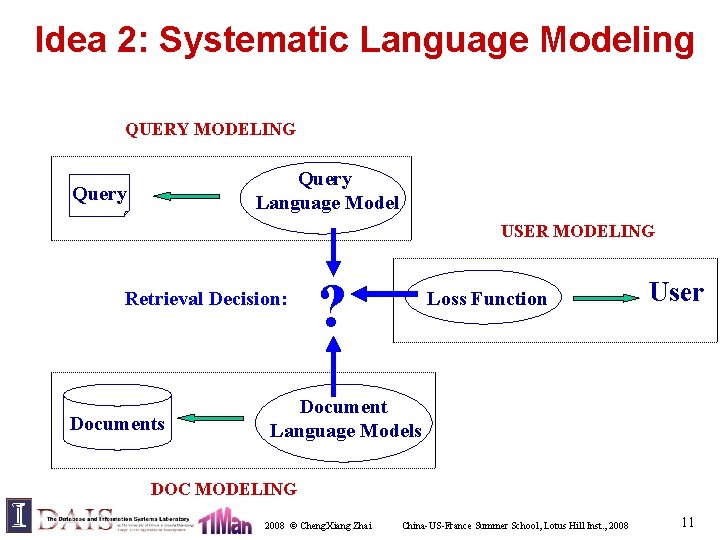
Idea 2: Systematic Language Modeling QUERY MODELING Query Language Model Query USER MODELING Retrieval Decision: Documents ? Loss Function User Document Language Models DOC MODELING 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 11

Generative Model of Document & Query [Lafferty & Zhai 01 b] Us er U q Partially observed Sourc e observed R d S Query Document inferred 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 12

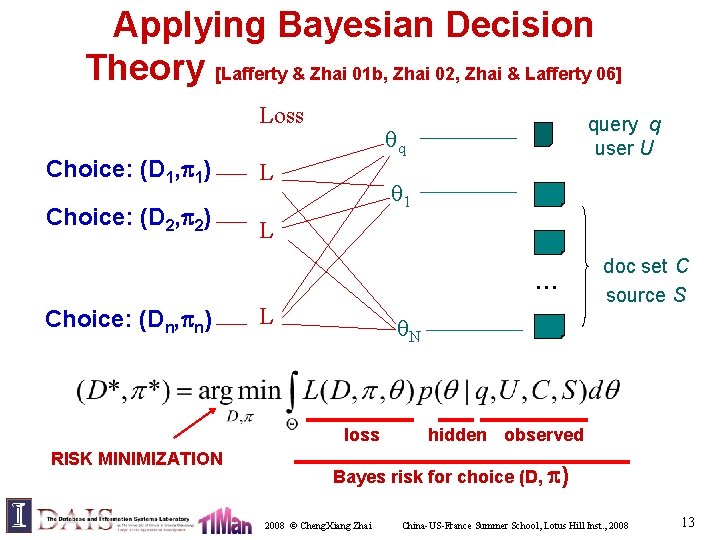
Applying Bayesian Decision Theory [Lafferty & Zhai 01 b, Zhai 02, Zhai & Lafferty 06] Loss Choice: (D 1, 1) L Choice: (D 2, 2) L query q user U q 1 . . . Choice: (Dn, n) L N loss RISK MINIMIZATION doc set C source S hidden observed Bayes risk for choice (D, ) 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 13

Benefits of the Framework • Systematic exploration of retrieval models (covering almost all the existing retrieval models as special cases) • Derive general retrieval principles (risk ranking principle) • Automatic parameter setting • Go beyond independent-relevance (subtopic retrieval) 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 14

Special Cases of Risk Minimization • Set-based models (choose D) • Ranking models (choose ) – Independent loss Probabilistic relevance model Generative Relevance Theory Vector-space Model Two-stage LM KL-divergence model • Relevance-based loss • Distance-based loss – Dependent loss • MMR loss • MDR loss Boolean model Subtopic retrieval model 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 15

Case 1: Two-stage Language Models Loss function U Risk ranking formula q Stage 2: compute Stage 2 (Mixture model) Stage 1 S d Stage 1: compute Two-stage smoothing (Dirichlet prior smoothing) 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 16

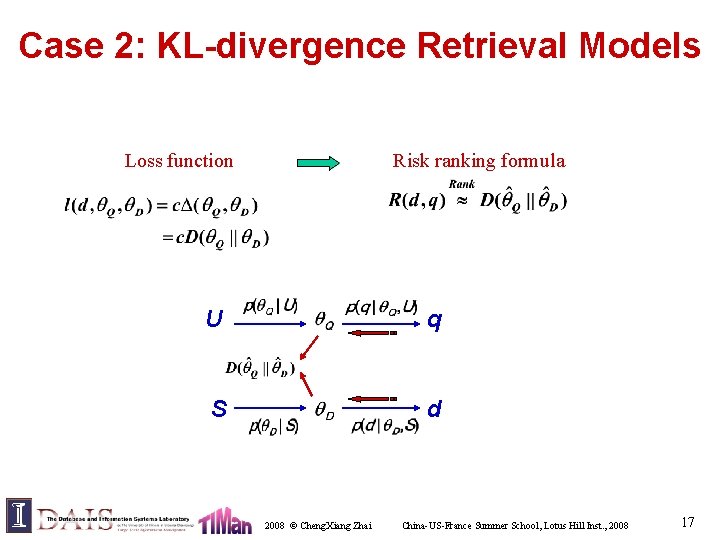
Case 2: KL-divergence Retrieval Models Loss function Risk ranking formula U q S d 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 17

Case 3: Aspect Generative Model of Document & Query Us er U Sourc e q Query d Document =( 1, …, k) S PLSI: LDA: 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 18

Optimal Ranking for Independent Loss Decision space = {rankings} Sequential browsing Independent loss Independent risk = independent scoring “Risk ranking principle” [Zhai 02] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 19

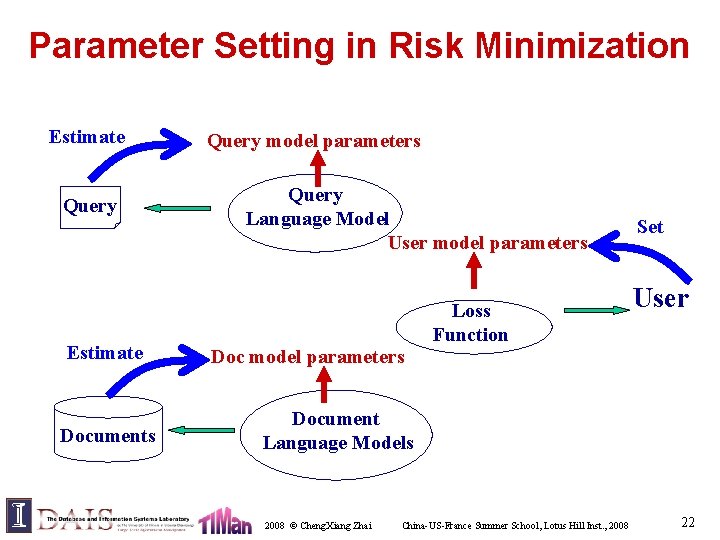
Automatic Parameter Tuning • Retrieval parameters are needed to – model different user preferences – customize a retrieval model to specific queries and documents • Retrieval parameters in traditional models – EXTERNAL to the model, hard to interpret – Parameters are introduced heuristically to implement “intuition” – No principles to quantify them, must set empirically through many experiments – Still no guarantee for new queries/documents • Language models make it possible to estimate parameters… 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 20

The Way to Automatic Tuning. . . • Parameters must be PART of the model! – Query modeling (explain difference in query) – Document modeling (explain difference in doc) • De-couple the influence of a query on parameter setting from that of documents – To achieve stable setting of parameters – To pre-compute query-independent parameters 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 21

Parameter Setting in Risk Minimization Estimate Query Estimate Documents Query model parameters Query Language Model User model parameters Doc model parameters Loss Function Set User Document Language Models 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 22

Generative Relevance Hypothesis [Lavrenko 04] • • • Generative Relevance Hypothesis: – For a given information need, queries expressing that need and documents relevant to that need can be viewed as independent random samples from the same underlying generative model A special case of risk minimization when document models and query models are in the same space Implications for retrieval models: “the same underlying generative model” makes it possible to – Match queries and documents even if they are in different languages or media – Estimate/improve a relevant document model based on example queries or vice versa 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 23

Risk minimization can easily go beyond independent relevance… 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 24

Aspect Retrieval Query: What are the applications of robotics in the world today? Find as many DIFFERENT applications as possible. Aspect judgments Example Aspects: A 1: spot-welding robotics A 2: controlling inventory A 3: pipe-laying robots A 4: talking robot A 5: robots for loading & unloading memory tapes A 6: robot [telephone] operators A 7: robot cranes …… d 1 d 2 d 3 …. dk A 1 A 2 A 3 …. . . Ak 1 1 0 0… 0 0 0 1 1 1… 0 0 0… 1 0 1 0. . . 0 1 Must go beyond independent relevance! 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 25

Evaluation Measures • Aspect Coverage (AC): measures per-doc coverage – #distinct-aspects/#docs – Equivalent to the “set cover” problem, NP-hard • Aspect Uniqueness(AU): measures redundancy – #distinct-aspects/#aspects – Equivalent to the “volume cover” problem, NP-hard • 0 0 d 1 01 0 0 1 #doc 1 #asp 2 #uniq-asp 2 AC: 2/1=2. 0 AU: 2/2=1. 0 Examples Accumulated counts 0 1 d 2 01 1 0 0 2 5 4 4/2=2. 0 4/5=0. 8 2008 © Cheng. Xiang Zhai 1 0 d 3 00 1 3 8 5 5/3=1. 67 5/8=0. 625 …. . . …… …… China-US-France Summer School, Lotus Hill Inst. , 2008 26

Dependent Relevance Ranking • In general, the computation of the optimal ranking is NP-hard • A general greedy algorithm – Pick the first document according to INDEPENDENT relevance – Given that we have picked k documents, evaluate the CONDITIONAL relevance of each candidate document – Choose the document that has the highest conditional relevance value 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 27

Loss Function L( k+1 | 1 … k ) known d 1 dk ? dk+1 … Maximal Marginal Relevance (MMR) 1 k k+1 Novelty/Redundancy Nov ( k+1 | 1 … k ) The best dk+1 is novel & relevant Relevance Rel( k+1 ) Maximal Diverse Relevance (MDR) 1 Aspect Coverage Distrib. p(a| i) The best dk+1 is complementary in coverage k k+1 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 28

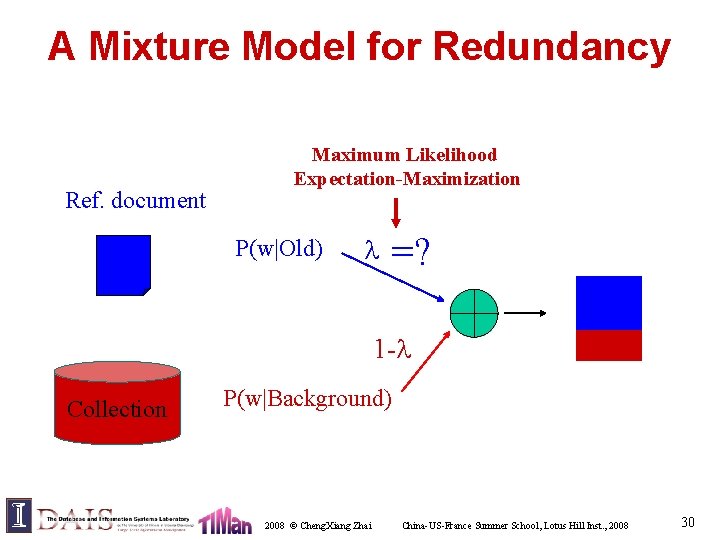
Maximal Marginal Relevance (MMR) Models • Maximizing aspect coverage indirectly through redundancy elimination • Conditional-Rel. = novel + relevant • Elements – Redundancy/Novelty measure – Combination of novelty and relevance 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 29

A Mixture Model for Redundancy Ref. document Maximum Likelihood Expectation-Maximization P(w|Old) =? 1 - Collection P(w|Background) 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 30

Cost-based Combination of Relevance and Novelty Relevance score 2008 © Cheng. Xiang Zhai Novelty score China-US-France Summer School, Lotus Hill Inst. , 2008 31

Maximal Diverse Relevance (MDR) Models • Maximizing aspect coverage directly through aspect modeling • Conditional-rel. = complementary coverage • Elements – Aspect loss function – Generative Aspect Model 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 32

Aspect Generative Model of Document & Query Us er U Sourc e q Query d Document =( 1, …, k) S PLSI: LDA: 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 33

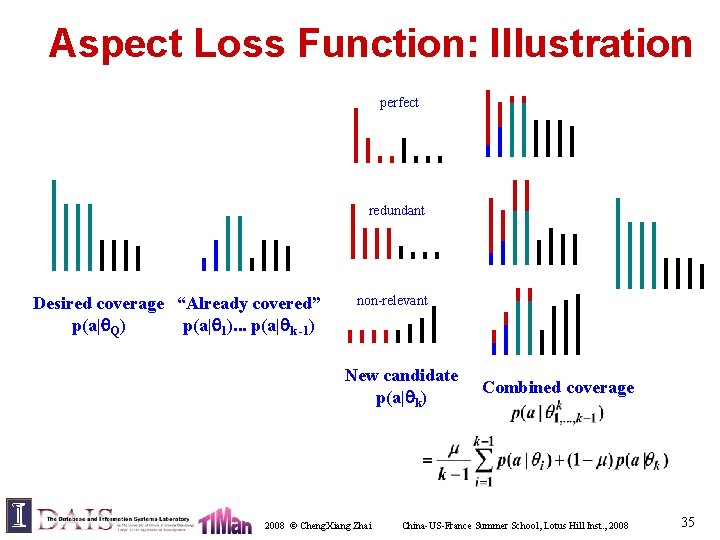
Aspect Loss Function U q S d 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 34

Aspect Loss Function: Illustration perfect redundant Desired coverage “Already covered” p(a| Q) p(a| 1). . . p(a| k -1) non-relevant New candidate p(a| k) 2008 © Cheng. Xiang Zhai Combined coverage China-US-France Summer School, Lotus Hill Inst. , 2008 35

Risk Minimization: Summary • Risk minimization is a general probabilistic retrieval framework – Retrieval as a decision problem (=risk min. ) – Separate/flexible language models for queries and docs • Advantages – A unified framework for existing models – Automatic parameter tuning due to LMs – Allows for modeling complex retrieval tasks • • Lots of potential for exploring LMs… For more information, see [Zhai 02] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 36

Future Research Directions • Modeling latent structures of documents – Introduce source structures (naturally suggest structure-based smoothing methods) • Modeling multiple queries and clickthroughs of the same user – Let the observation include multiple queries and clickthroughs • Collaborative search – Introduce latent interest variables to tie similar users together • Modeling interactive search 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 37

Axiomatic Retrieval Framework Most of the following slides are from Hui Fang’s presentation 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 38

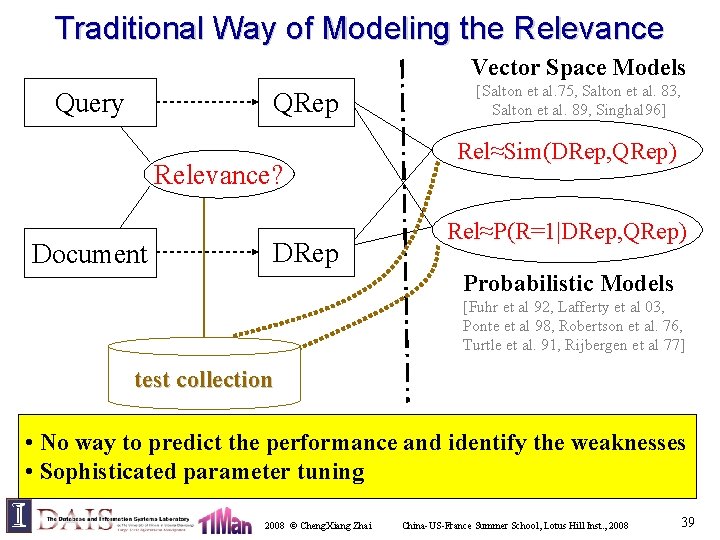
Traditional Way of Modeling the Relevance Vector Space Models Query QRep Relevance? Document DRep [Salton et al. 75, Salton et al. 83, Salton et al. 89, Singhal 96] Rel≈Sim(DRep, QRep) Rel≈P(R=1|DRep, QRep) Probabilistic Models [Fuhr et al 92, Lafferty et al 03, Ponte et al 98, Robertson et al. 76, Turtle et al. 91, Rijbergen et al 77] test collection • No way to predict the performance and identify the weaknesses • Sophisticated parameter tuning 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 39

No Way to Predict the Performance 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 40

Sophisticated Parameter Tuning “k 1, b and k 3 are parameters which depend on the nature of the queries and possibly on the database; k 1 and b default to 1. 2 and 0. 75 respectively, but smaller values of b are sometimes advantageous; in long queries k 3 is often set to 7 or 1000. ” [Robertson et al. 1999] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 41

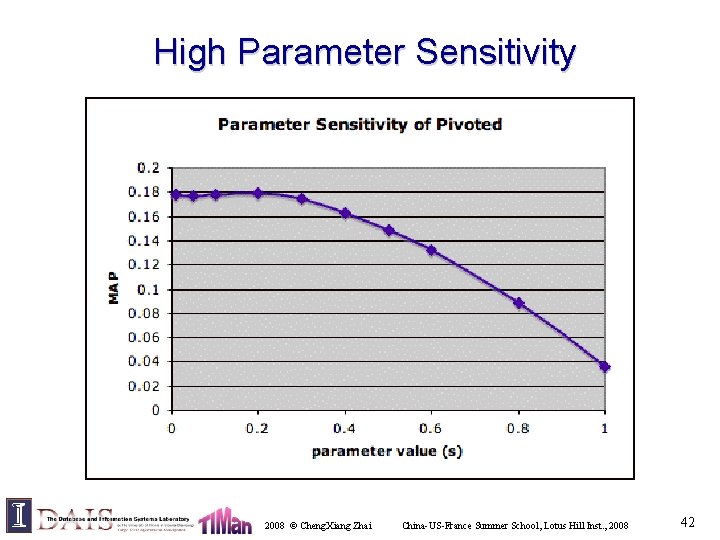
High Parameter Sensitivity 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 42

Hui Fang’s Thesis Work [Fang 07] Propose a novel axiomatic framework, where relevance is directly modeled with term-based constraints – Predict the performance of a function analytically [Fang et al. , SIGIR 04] – Derive more robust and effective retrieval functions [Fang & Zhai, SIGIR 05, Fang & Zhai, SIGIR 06] – Diagnose weaknesses and strengths of retrieval functions [Fang & Zhai, under review] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 43

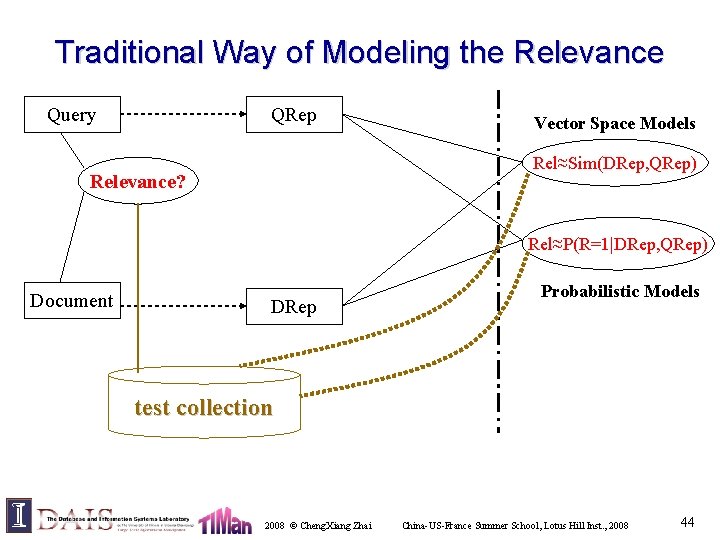
Traditional Way of Modeling the Relevance Query QRep Vector Space Models Rel≈Sim(DRep, QRep) Relevance? Rel≈P(R=1|DRep, QRep) Document DRep Probabilistic Models test collection 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 44

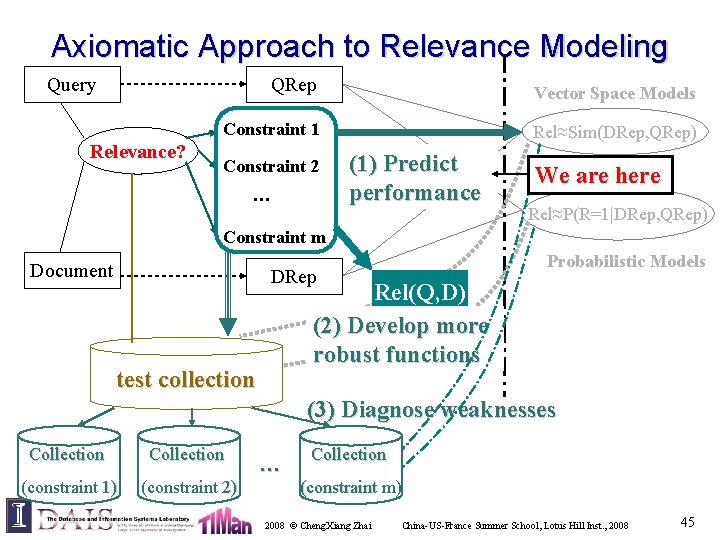
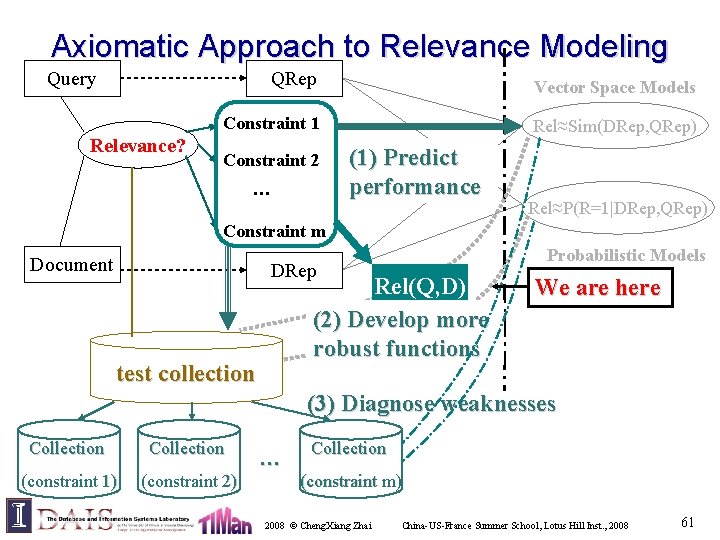
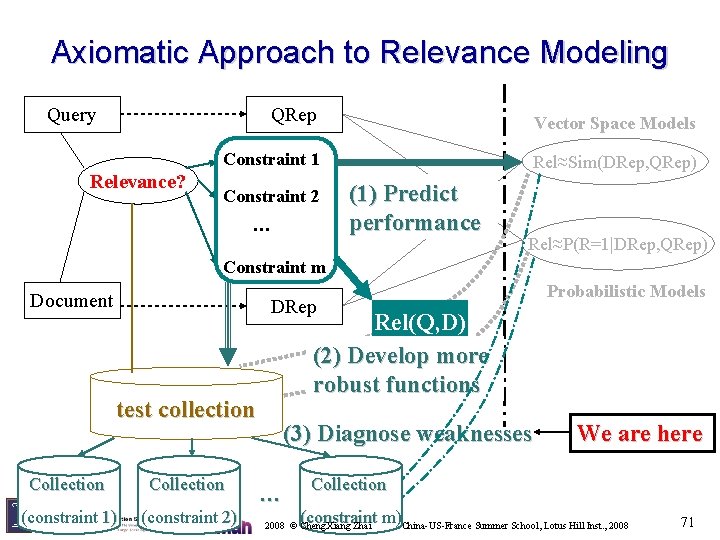
Axiomatic Approach to Relevance Modeling Query Relevance? QRep Vector Space Models Constraint 1 Rel≈Sim(DRep, QRep) Constraint 2 … (1) Predict performance We are here Rel≈P(R=1|DRep, QRep) Constraint m Document Probabilistic Models DRep Rel(Q, D) (2) Develop more robust functions test collection (3) Diagnose weaknesses Collection (constraint 1) (constraint 2) … Collection (constraint m) 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 45

Part 1: Define retrieval constraints [Fang et. al. SIGIR 2004] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 46

Empirical Observations in IR (Cont. ) • Pivoted Normalization Method 1+ln(c(w, d)) • Dirichlet Prior Method • Okapi Method 2008 © Cheng. Xiang Zhai Parameter sensitivity Document Inversed Alternative Term Length Document TF Frequency transformation Normalization Frequency China-US-France Summer School, Lotus Hill Inst. , 2008 47

Research Questions • How can we formally characterize these necessary retrieval heuristics? • Can we predict the empirical behavior of a method without experimentation? 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 48

Term Frequency Constraints (TFC 1) TF weighting heuristic I: Give a higher score to a document with more occurrences of a query term. • TFC 1 Let q be a query with only one term w. If and q: w d 1: d 2: then 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 49

Term Frequency Constraints (TFC 2) TF weighting heuristic II: Favor a document with more distinct query terms. • TFC 2 Let q be a query and w 1, w 2 be two query terms. Assume and If and q: w 1 w 2 d 1: d 2: then 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 50

Term Discrimination Constraint (TDC) IDF weighting heuristic: Penalize the words popular in the collection; Give higher weights to discriminative terms. Query: SVM Tutorial IDF(SVM)>IDF(Tutorial) Doc 1 Assume Doc 2 … … Tutorial SVM Tutorial … . . . … SVM SVM Tutorial … 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 51

Term Discrimination Constraint (Cont. ) • TDC Let q be a query and w 1, w 2 be two query terms. q: w 1 w 2 Assume and If for all other words w. d 1: d 2: and then 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 52

Length Normalization Constraints(LNCs) Document length normalization heuristic: Penalize long documents(LNC 1); Avoid over-penalizing long documents (LNC 2). • LNC 1 Let q be a query. If for some word q: d 1: d 2: but for other words then • LNC 2 Let q be a query. If q: d 1: d 2: and then 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 53

TF-LENGTH Constraint (TF-LNC) TF-LN heuristic: Regularize the interaction of TF and document length. • TF-LNC Let q be a query with only one term w. If q: w d 1: d 2: and then 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 54

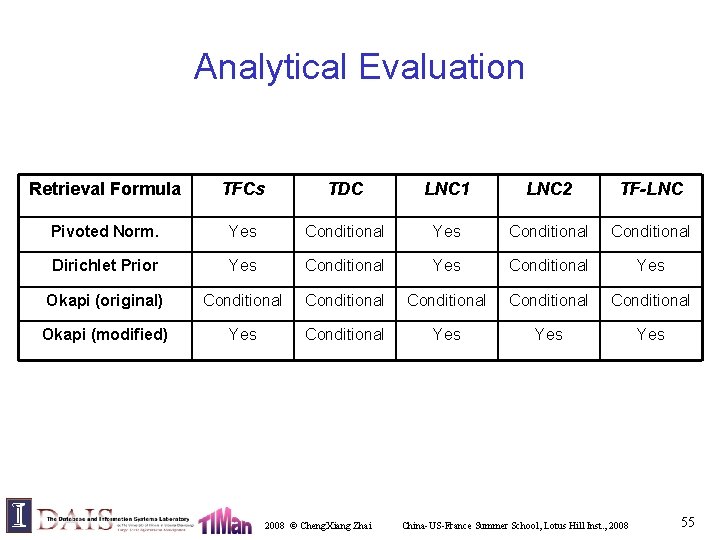
Analytical Evaluation Retrieval Formula TFCs TDC LNC 1 LNC 2 TF-LNC Pivoted Norm. Yes Conditional Dirichlet Prior Yes Conditional Yes Okapi (original) Conditional Conditional Okapi (modified) Yes Conditional Yes Yes 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 55

Term Discrimination Constraint (TDC) IDF weighting heuristic: Penalize the words popular in the collection; Give higher weights to discriminative terms. Query: SVM Tutorial IDF(SVM)>IDF(Tutorial) Doc 1 Assume Doc 2 … … Tutorial SVM Tutorial … . . . … SVM SVM Tutorial … 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 56

Benefits of Constraint Analysis • Provide an approximate bound for the parameters – A constraint may be satisfied only if the parameter is within a particular interval. • Compare different formulas analytically without experimentations – When a formula does not satisfy the constraint, it often indicates non-optimality of the formula. • Suggest how to improve the current retrieval models – Violation of constraints may pinpoint where a formula needs to be improved. 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 57

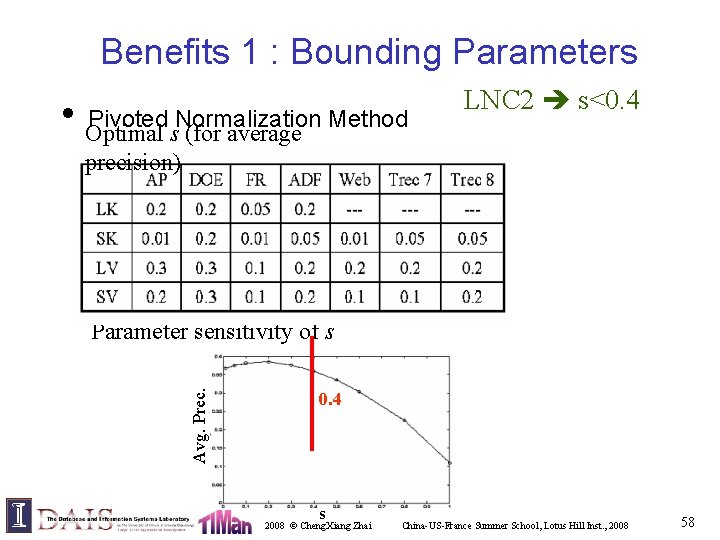
Benefits 1 : Bounding Parameters • Optimal Pivoted Normalization Method s (for average LNC 2 s<0. 4 precision) Avg. Prec. Parameter sensitivity of s 0. 4 s 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 58

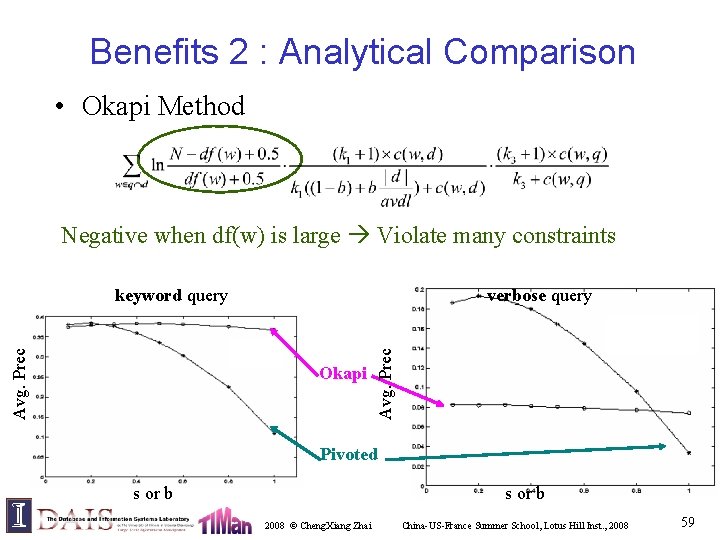
Benefits 2 : Analytical Comparison • Okapi Method Negative when df(w) is large Violate many constraints verbose query Okapi Avg. Prec keyword query Pivoted s or b 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 59

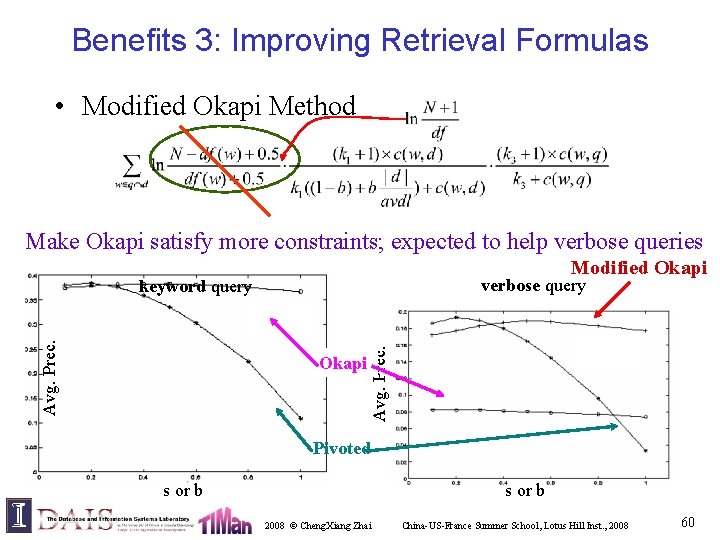
Benefits 3: Improving Retrieval Formulas • Modified Okapi Method Make Okapi satisfy more constraints; expected to help verbose queries Modified Okapi verbose query Okapi Avg. Prec. keyword query Pivoted s or b 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 60

Axiomatic Approach to Relevance Modeling Query Relevance? QRep Vector Space Models Constraint 1 Rel≈Sim(DRep, QRep) Constraint 2 … (1) Predict performance Rel≈P(R=1|DRep, QRep) Constraint m Document Probabilistic Models DRep Rel(Q, D) (2) Develop more robust functions test collection We are here (3) Diagnose weaknesses Collection (constraint 1) (constraint 2) … Collection (constraint m) 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 61

Part 2: Derive new retrieval functions [Fang & Zhai SIGIR 05, Fang & Zhai SIGIR 06] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 62

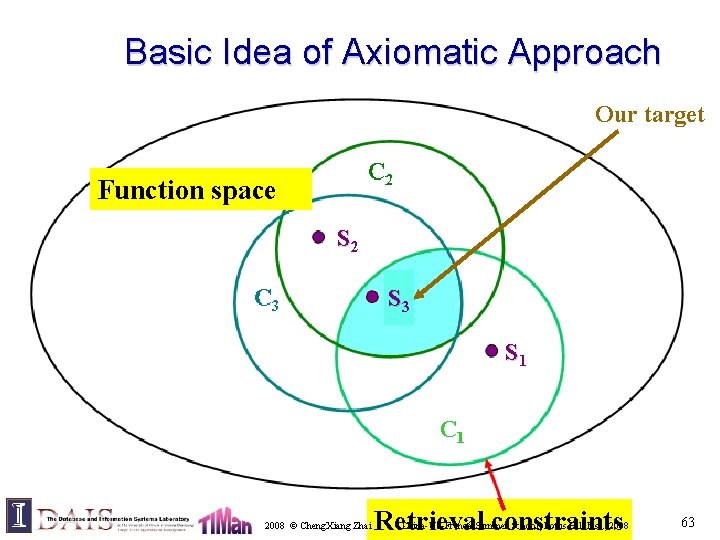
Basic Idea of Axiomatic Approach Our target C 2 Functionspace Function S 22 C 3 SS 33 SS 11 C 1 2008 © Cheng. Xiang Zhai Retrieval constraints China-US-France Summer School, Lotus Hill Inst. , 2008 63

Function Space Define the function space inductively Q: cat big D: dog big Primitive weighting function (f) S(Q, D) = S( , ) = f ( , ) Query growth function (h) S(Q, D) = S( , )+h( , , ) )+g( , , ) Document growth function (g) S(Q, D) = S( , 2008 © Cheng. Xiang Zhai ) = S( , China-US-France Summer School, Lotus Hill Inst. , 2008 64

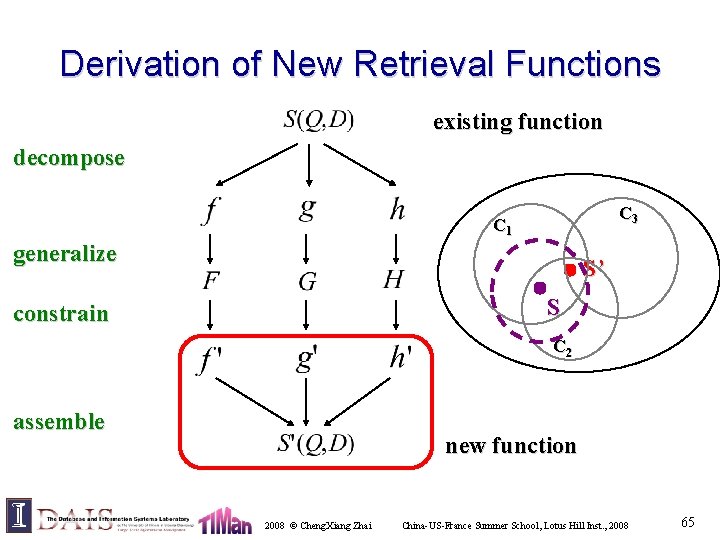
Derivation of New Retrieval Functions existing function decompose C 3 C 1 generalize S’ S constrain C 2 assemble new function 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 65

Representative Derived Function QTF IDF TF length normalization 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 66

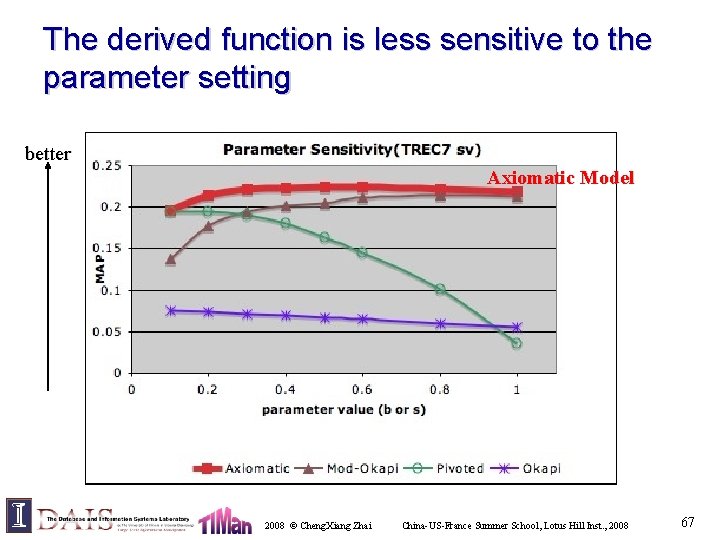
The derived function is less sensitive to the parameter setting better Axiomatic Model 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 67

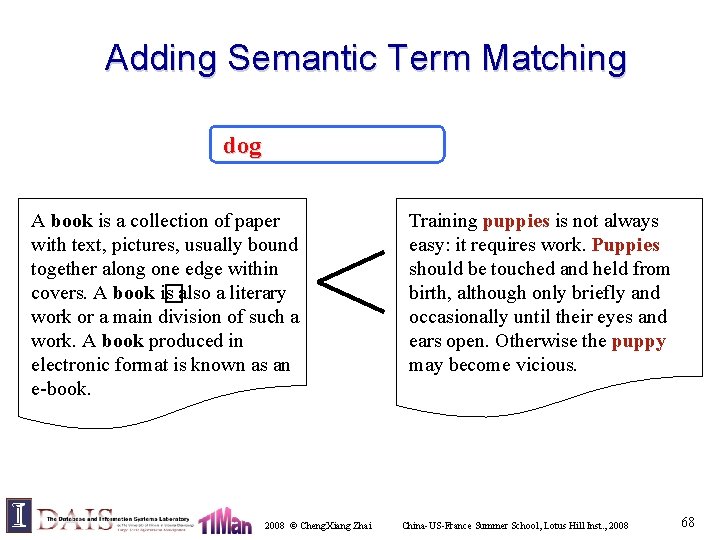
Adding Semantic Term Matching dog A book is a collection of paper with text, pictures, usually bound together along one edge within covers. A book is �also a literary work or a main division of such a work. A book produced in electronic format is known as an e-book. 2008 © Cheng. Xiang Zhai Training puppies is not always easy: it requires work. Puppies should be touched and held from birth, although only briefly and occasionally until their eyes and ears open. Otherwise the puppy may become vicious. China-US-France Summer School, Lotus Hill Inst. , 2008 68

General Approach to Semantic Term Matching • Select semantic similar terms • Expand original query with the selected terms dog 1 puppy 0. 5 doggy 0. 5 hound 0. 5 bone Key challenge: How to weight selected terms? 0. 1 The proposed axiomatic approach provides guidance on how to weight terms appropriately. 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 69

Effectiveness of Semantic Term Matching ROBUST 04 Syntactic term matching ROBUST 05 MAP P@20 0. 248 0. 352 0. 192 0. 379 0. 302 0. 399 0. 292 0. 502 (baseline) Semantic term matching (21. 8%) 2008 © Cheng. Xiang Zhai (51. 0%) China-US-France Summer School, Lotus Hill Inst. , 2008 70

Axiomatic Approach to Relevance Modeling Query Relevance? QRep Vector Space Models Constraint 1 Rel≈Sim(DRep, QRep) Constraint 2 … (1) Predict performance Rel≈P(R=1|DRep, QRep) Constraint m Document DRep test collection Collection (constraint 1) (constraint 2) Probabilistic Models Rel(Q, D) (2) Develop more robust functions (3) Diagnose weaknesses … We are here Collection (constraint m)China-US-France Summer School, Lotus Hill Inst. , 2008 © Cheng. Xiang Zhai 71

Part 3: Diagnostic evaluation for IR models [Fang & Zhai, under review] 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 72

Existing evaluation provides little explanation for the performance differences test collection Query: dog Doc 1: Retrieval Function MAP=0. 25 Doc 2: … Docn: trec 8 wt-2 g fr 88 -89 Pivoted 0. 244 0. 288 0. 218 Dirichlet 0. 257 0. 302 0. 202 How to diagnose weaknesses and strengths of retrieval functions? 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 73

Relevance-Preserving Perturbations Perturb term statistics in documents and keep relevance status document scaling perturbation: c. D(d, d, K) concatenate every document with itself K times 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 74

Summary of Perturbations • • • Relevance addition Noise addition Internal term growth Document scaling Relevant document concatenation Non-relevant document concatenation Noise deletion Document addition Document deletion 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 75

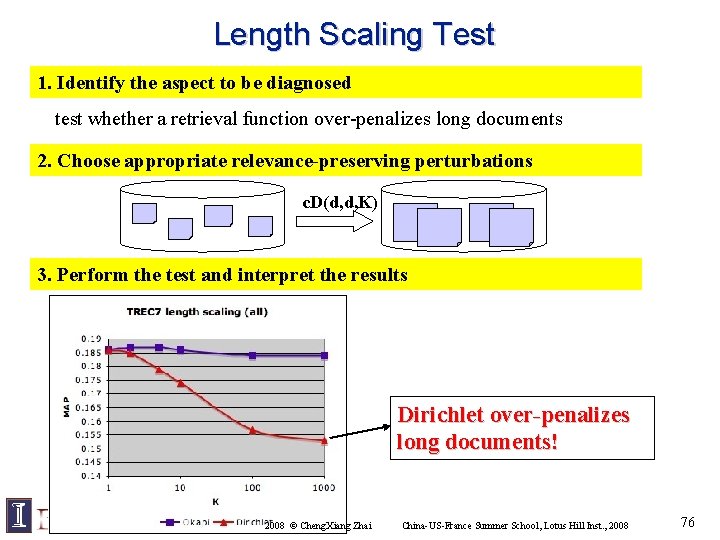
Length Scaling Test 1. Identify the aspect to be diagnosed test whether a retrieval function over-penalizes long documents 2. Choose appropriate relevance-preserving perturbations c. D(d, d, K) 3. Perform the test and interpret the results Dirichlet over-penalizes long documents! 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 76

Summary of Diagnostic Tests • Length variation sensitivity tests – Length variance reduction test – Length variance amplification test – Length scaling test • Term noise resistance tests – Term noise addition test • TF-LN balance Tests – Single query term growth – Majority query term growth – All query term growth 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 77

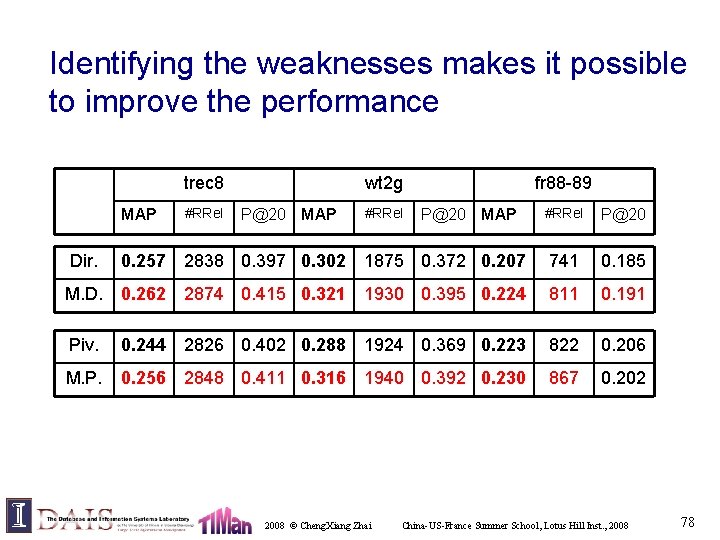
Identifying the weaknesses makes it possible to improve the performance trec 8 MAP #RRel wt 2 g P@20 MAP #RRel fr 88 -89 P@20 MAP #RRel P@20 Dir. 0. 257 2838 0. 397 0. 302 1875 0. 372 0. 207 741 0. 185 M. D. 0. 262 2874 0. 415 0. 321 1930 0. 395 0. 224 811 0. 191 Piv. 0. 244 2826 0. 402 0. 288 1924 0. 369 0. 223 822 0. 206 M. P. 0. 256 2848 0. 411 0. 316 1940 0. 392 0. 230 867 0. 202 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 78

Axiomatic Framework: Summary • A new way of examining and developing retrieval models • Facilitate analytical study of retrieval models • Applicable to the development of all kinds of ranking functions • Limitation: – Constraints can be subjective – Not constructive (thus must rely on other techniques to reduce the search space) • Combined with machine learning? 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 79

Lecture 4: Key Points • Retrieval problem can be generally formalized as a statistical decision problem – Nicely incorporate generative models into a retrieval framework – Serve as a road map for exploring new retrieval models – Make it easier to model complex retrieval problems (interactive retrieval) • Axiomatic framework makes it possible to analyze a retrieval function without experimentation – Facilitate theoretical study of retrieval models (“impossibility theorem”? ) – Offer a general methodology for thinking about and improving retrieval models 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 80

Readings • The risk minimization paper: – http: //sifaka. cs. uiuc. edu/czhai/riskmin. pdf • Hui Fang’s thesis: – http: //www. cs. uiuc. edu/techreports. php? report=UIUCD CS-R-2007 -2847 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 81

Discussion • Risk minimization for multimedia retrieval – Add generative models of images and video to the framework – Unifying multimedia with text as a common language • Axiomatic approaches – Constraints for ranking multimedia information items – Add constraints to a statistical learning framework (e. g. , add constraints as prior or regularization) 2008 © Cheng. Xiang Zhai China-US-France Summer School, Lotus Hill Inst. , 2008 82