Inflation and String Cosmology Andrei Linde Why do
























- Slides: 34

Inflation and String Cosmology Andrei Linde

Why do we need inflation? Problems of the standard Big Bang theory: What was before the Big Bang? Why is our universe so homogeneous (better than 1 part in 10000) ? Why is it isotropic (the same in all directions)? Why all of its parts started expanding simultaneously? Why it is flat? flat Why parallel lines do not intersect? Why it contains so many particles?

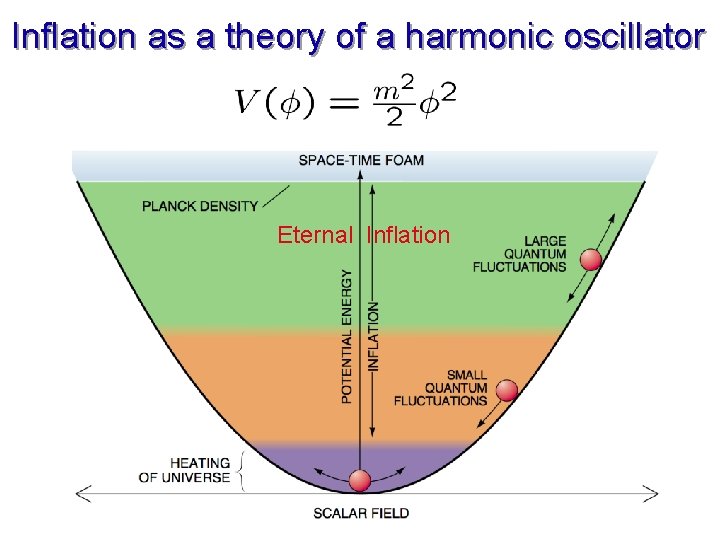
Inflation as a theory of a harmonic oscillator Eternal Inflation

Equations of motion: Einstein: Klein-Gordon: Compare with equation for the harmonic oscillator with friction:

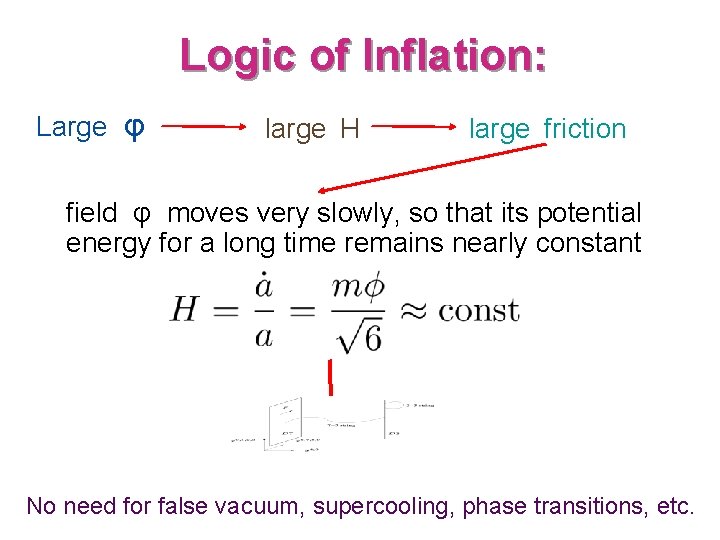
Logic of Inflation: Large φ large H large friction field φ moves very slowly, so that its potential energy for a long time remains nearly constant No need for false vacuum, supercooling, phase transitions, etc.

Predictions of Inflation: 1) The universe should be homogeneous, isotropic and flat, = 1 + O(10 -4) [ Observations: the universe is homogeneous, isotropic and flat, = 1 + O(10 -2) • Inflationary perturbations should be gaussian and adiabatic, with flat spectrum, ns = 1+ O(10 -1) Observations: perturbations are gaussian and adiabatic, with flat spectrum, ns = 1 + O(10 -2)

Tensor Perturbations? In the simplest chaotic inflation model the ratio of tensor to scalar perturbations is r = 0. 13 In almost all other models r is incredibly small, which makes finding B-mode rather problematic At present, the bet for finding B-mode looks like a bet for simplicity (simplest chaotic inflation) versus sophistication (almost everything else)

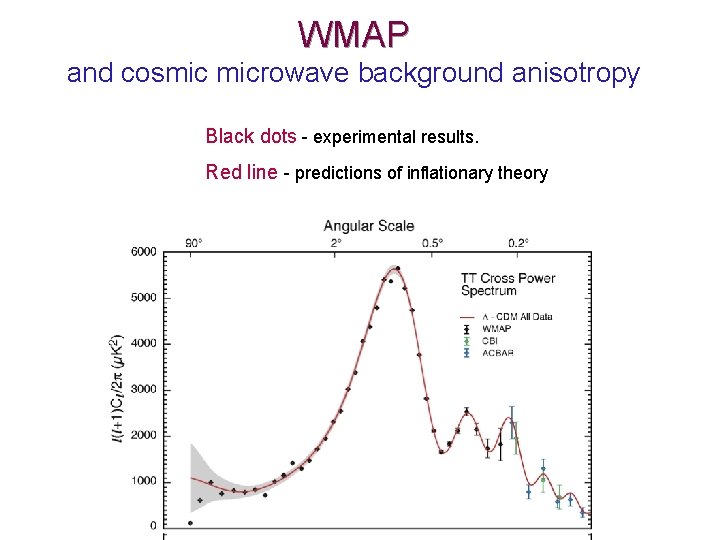
WMAP and cosmic microwave background anisotropy Black dots - experimental results. Red line - predictions of inflationary theory

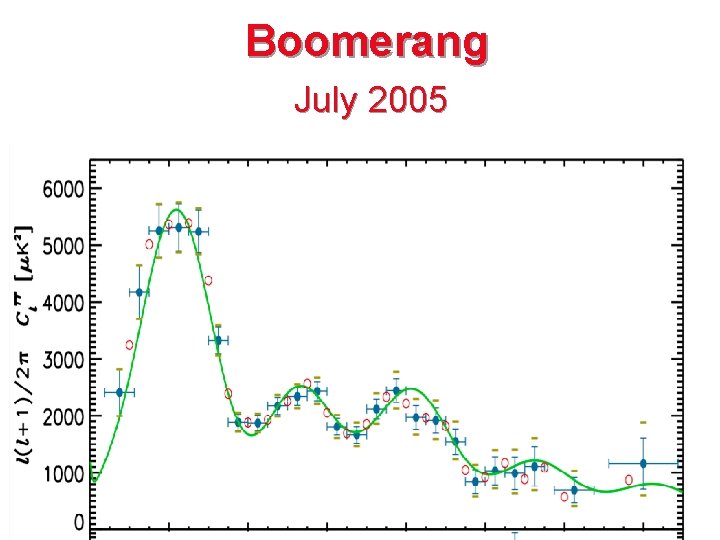
Boomerang July 2005

Name Recognition Alex Vilenkin Stephen Hawking

Inflation in String Theory The volume stabilization problem: A potential of theory obtained by compactification in string theory of type IIB: X and Y are canonically normalized field corresponding to the dilaton field and to the volume of the compactified space; is the field driving inflation The potential with respect to X and Y is very steep, these fields rapidly run down, and the potential energy V vanishes. We must stabilize these fields. Dilaton stabilization: Volume stabilization: Giddings, Kachru, Polchinski 2001 KKLT construction Kachru, Kallosh, A. L. , Trivedi 2003 Burgess, Kallosh, Quevedo, 2003

Volume stabilization Kachru, Kallosh, A. L. , Trivedi 2003 Basic steps of the KKLT scenario: 1) Start with a theory with runaway potential discussed above 2) Bend this potential down due to (nonperturbative) quantum effects 1. 3) Uplift the minimum to the state with positive vacuum energy by adding a positive energy of an anti-D 3 brane in warped Calabi-Yau space Ad. S minimum Metastable d. S minimum

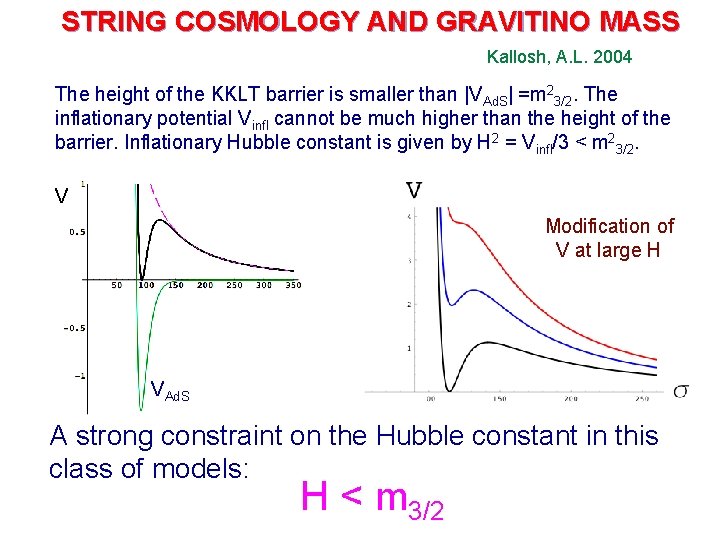
STRING COSMOLOGY AND GRAVITINO MASS Kallosh, A. L. 2004 The height of the KKLT barrier is smaller than |VAd. S| =m 23/2. The inflationary potential Vinfl cannot be much higher than the height of the barrier. Inflationary Hubble constant is given by H 2 = Vinfl/3 < m 23/2. V Modification of V at large H VAd. S A strong constraint on the Hubble constant in this class of models: H < m 3/2

But do we have stability even before inflation? Finding supersymmetric Ad. S extrema before uplifting does not imply positivity of the mass matrix. For example, if one fixes the dilaton by fluxes and after that fixes the volume, one may get instability. Choi, Falkowski, Nilles, Olechowski, Pokorski 2004 There are known examples where all moduli are stable after uplifting, but one should check it for each new model. A possible way to solve this problem once and for all is to consider supersymmetric Minkowski vacua instead of Ad. S. If one finds such a state, it is automatically stable.

Why supersymmetry of Minkowski vacuum implies stability? In a supersymmetric Minkowski extremum at one has If one deviates by from the position of this extremum, one always finds that is higher order in than Therefore in a vicinity of one has That is why the supersymmetric state with V = 0 is stable.

A new class of KKLT models Kallosh, A. L. hep-th/0411011 Using racetrack superpotential with two exponents one can obtain a supersymmetric Minkowski vacuum without any uplifting of the potential Inflation in the new class of KKLT models can occur at H >> m 3/2 No correlation between the gravitino mass, the height of the barrier and the Hubble constant during inflation

Adding axion-dilaton and complex moduli Kallosh, A. L. , Pillado, hep-th/0511042 Solutions of these equations preserve supersymmetry in Minkowski space, which guarantees vacuum stability.

Main conclusions after 2 years of investigation: It is possible to stabilize internal dimensions, and obtain an accelerating universe. Eventually, our part of the universe will decay and become 10120 ten-dimensional, but it will only happen in 10 years Apparently, vacuum stabilization can be achieved in 10100 - 101000 different ways. This means that the potential energy V of string theory may have 10100 - 101000 minima where we (or somebody else) can enjoy life…

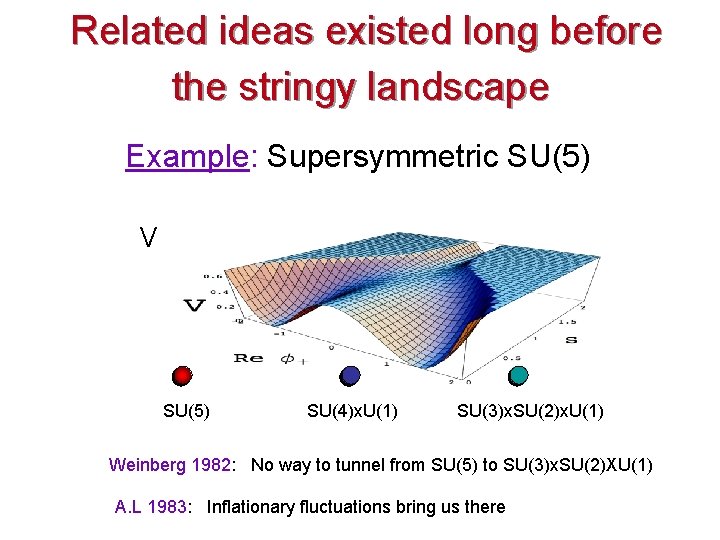
Related ideas existed long before the stringy landscape Example: Supersymmetric SU(5) V SU(5) SU(4)x. U(1) SU(3)x. SU(2)x. U(1) Weinberg 1982: No way to tunnel from SU(5) to SU(3)x. SU(2)XU(1) A. L 1983: Inflationary fluctuations bring us there

Self-reproducing Inflationary Universe

It was never easy to discuss anthropic principle, even with friends… But recently the concept of the string theory landscape came to the rescue

String Theory Landscape Perhaps 10100 - 101000 different minima Lerche, Lust, Schellekens 1987 Bousso, Polchinski; Susskind; Douglas, Denef, …

Curvaton Web Usually people believe that the amplitude of inflationary perturbations is constant, ~ 10 -5 everywhere. However, in the curvaton version of inflationary scenario the value of is different in different exponentially large parts of the universe. A. L. , Mukhanov, astro-ph/0511736

Dark matter Example: Dark matter in the axion field. Standard lore: If the axion mass is smaller than 10 -5 e. V, the amount of dark matter in the axion field contradicts observations, for a typical initial value of the axion field. Anthropic argument: We cannot live in the parts of the universe with a typical initial value of the axion field. We can live only in those rare parts where the initial value of the axion field was sufficiently small to ensure that This is what we see now. Without anthropic arguments, it would look like a miracle. A. L. 1988, Aguirre, Rees, Tegmark, Wilczek (today in astro-ph)

Thus in addition to a DISCRETE set of parameters corresponding to 101000 vacua of string theory, we may have many CONTINUOUS parameters, such as the amplitude of density perturbations, the ratio of dark matter to baryons, etc. , which depend on cosmological dynamics. Some of these parameters are strongly constrained by anthropic principle.

Fundamental versus environmental Example: why do we live in a 3 D space? Karch, Randall: Only D 3 and D 7 branes survive after a cosmological dynamics of brane gas in Ad. S. We may live on D 3 or at the intersection of D 7, which may help to explain why our universe is 3 D. A problem: Friedmann universe dominated by a negative cosmological constant collapses together with all branes contained in it.

Anthropic approach to the same issue: Ehrenfest, 1917: Stable planetary and atomic systems are possible only in 3 D space. Indeed, for D > 3 planetary system are unstable, whereas for D < 3 there is NO gravity forces between stars and planets. This fact, in combination with inflation and string theory implies that if inflationary 3 D space-time is possible, then we should live in a 4 D space even if other compactifications are much more probable If one wants to suggest an alternative solution to a problem that is solved by anthropic principle, one is free to try. But it may be more productive to concentrate on many problems that do not have an anthropic solution

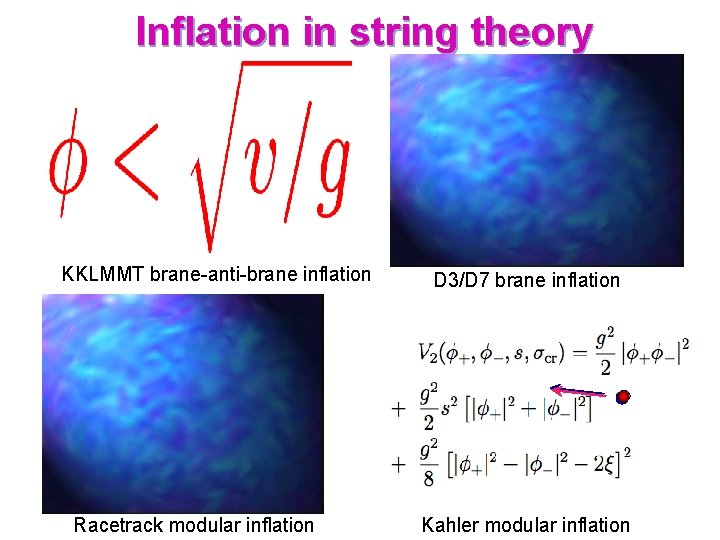
Two types of string inflation models: Moduli Inflation. Brane inflation. The simplest class of models. They use only the fields that are already present in the KKLT model. The inflaton field corresponds to the distance between branes in Calabi-Yau space. Historically, this was the first class of string inflation models.

Inflation in string theory KKLMMT brane-anti-brane inflation Racetrack modular inflation D 3/D 7 brane inflation Kahler modular inflation

Taking Advantage of Eternal Inflation in Stringy Landscape Eternal inflation is a general property of all landscapebased models: The fields eternally jump from one minimum to another, and the universe continues to expand exponentially. After a very long stage of cosmological evolution, the probability that the energy density at a given point is equal to V becomes given by the following “thermodynamic” expression (the square of the HH wave function): Here S is the Gibbons-Hawking entropy for d. S space. It does not require a modification proposed by Tye et al, and it does not describe quantum creation of the universe.

500 Let 10 flowers blossom > 0 < 0 = 0

However, at some point the fields must stop jumping, as in old inflation, and start rolling, as in new or chaotic inflation: the last stage of inflation must be of the slow-roll type. Otherwise we would live in an empty open universe with << 1. How can we create initial conditions for a slow-roll inflation after the tunneling?

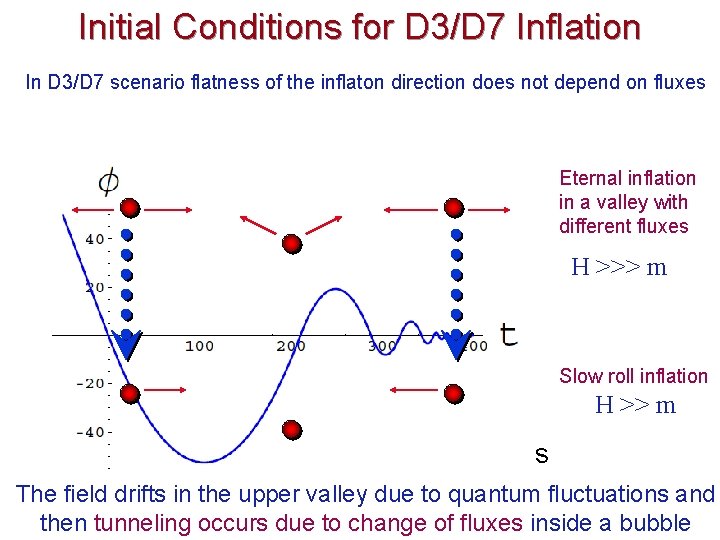
Initial Conditions for D 3/D 7 Inflation In D 3/D 7 scenario flatness of the inflaton direction does not depend on fluxes V Eternal inflation in a valley with different fluxes H >>> m Slow roll inflation H >> m s The field drifts in the upper valley due to quantum fluctuations and then tunneling occurs due to change of fluxes inside a bubble

The resulting scenario: 1) The universe eternally jumps from one d. S vacuum to another due to formation of bubbles. Each bubble contains a new d. S vacuum. The bubbles contain no particles unless this process ends by a stage of a slow-roll inflation. Here is how: 2) At some stage the universe appears in d. S state with a large potential but with a flat inflaton direction, as in D 3/D 7 model. Quantum fluctuations during eternal inflation in this state push the inflaton field S in all directions along the inflaton valley. 3) Eventually this state decays, and bubbles are produced. Each of these bubbles may contain any possible value of the inflaton field S, prepared by the previous stage. A slow-roll inflation begins and makes the universe flat. It produces particles, galaxies, and the participants of this conference: )
 Boltzmann brain theory
Boltzmann brain theory Licenseid=string&content=string&/paramsxml=string
Licenseid=string&content=string&/paramsxml=string Futa cum inflation
Futa cum inflation Hey hey bye bye
Hey hey bye bye Cosmology
Cosmology Critical density
Critical density Scale factor cosmology
Scale factor cosmology Axis of evil cosmology
Axis of evil cosmology Definition of cosmology
Definition of cosmology Cosmology
Cosmology Crossover cosmology
Crossover cosmology Concordance model of cosmology
Concordance model of cosmology Cosmology
Cosmology Cosmology
Cosmology Newton cosmology
Newton cosmology Cosmology
Cosmology Intro to cosmology
Intro to cosmology Jain geography universe
Jain geography universe Const char *s
Const char *s Public class person private name
Public class person private name String str
String str Linde pakistan limited
Linde pakistan limited Linde cryopump
Linde cryopump Fredrik linde
Fredrik linde Rudolf krause
Rudolf krause Merlin linde
Merlin linde Linde verfahren
Linde verfahren Merlin linde
Merlin linde Eesti
Eesti Carte de linde
Carte de linde Bioneer
Bioneer Linde meneghin
Linde meneghin Aei maj
Aei maj Why printing money causes inflation
Why printing money causes inflation Don't ask why why why
Don't ask why why why