Incremental formal verification of hardware Hana Chockler Alexander

Incremental formal verification of hardware Hana Chockler Alexander Ivrii Arie Matsliah Shiri Moran Ziv Nevo IBM Research - Haifa

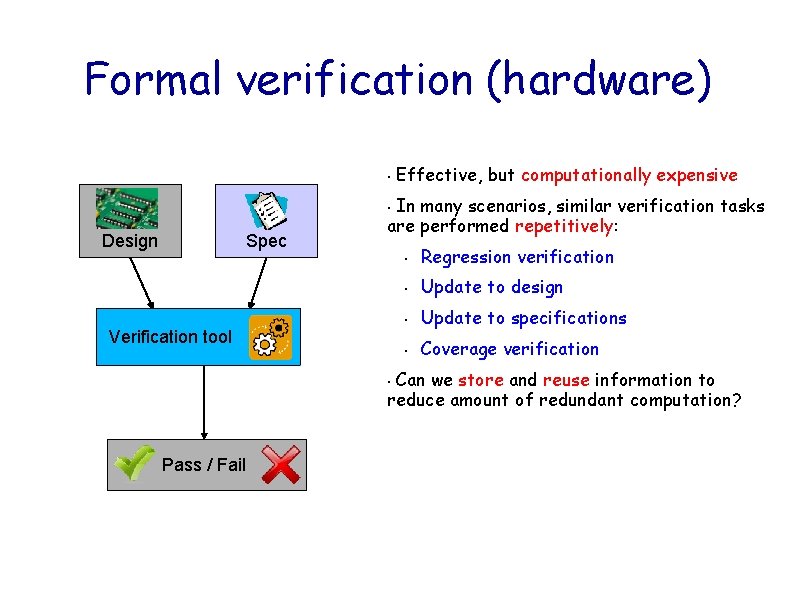
Formal verification (hardware) • Effective, but computationally expensive In many scenarios, similar verification tasks are performed repetitively: • Design Spec Verification tool • Regression verification • Update to design • Update to specifications • Coverage verification Can we store and reuse information to reduce amount of redundant computation? • Pass / Fail

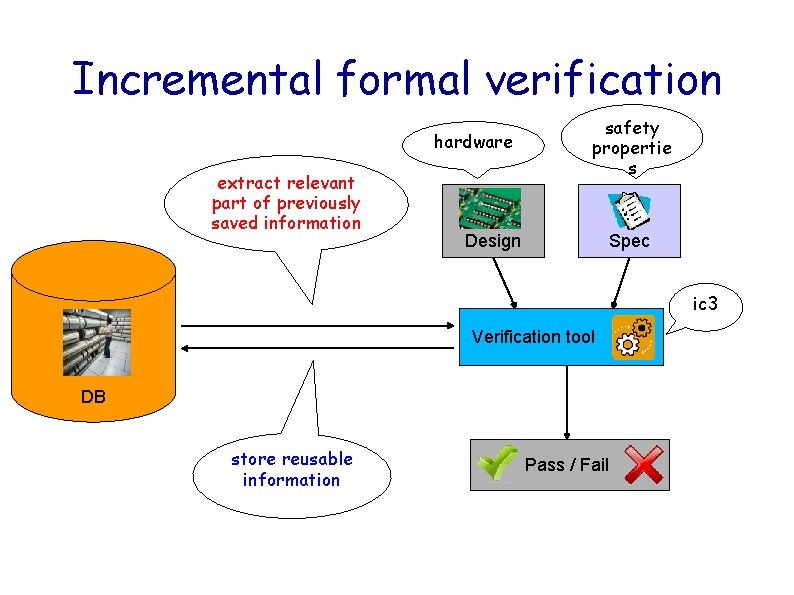
Incremental formal verification hardware extract relevant part of previously saved information safety propertie s Design Spec ic 3 Verification tool DB store reusable information Pass / Fail

Outline ● inductive proofs and inductive strengthening ● saving information ● ● – ic 3 overview – what is saved? reusing saved information – extracting relevant parts (w. r. t. new design/spec) – checking if verification can be concluded – injecting into ic 3 conclusion and experimental results

FSMs and safety properties ● ● ● T – transition relation R – all reachable states Ri – states reachable within i steps from I P – (safety) property R Rk-1 … t) ● I – initial states ┐P s, ● x 1, x 2, …, xn – state variables (latches) T( ● All states R 2 R 1 I

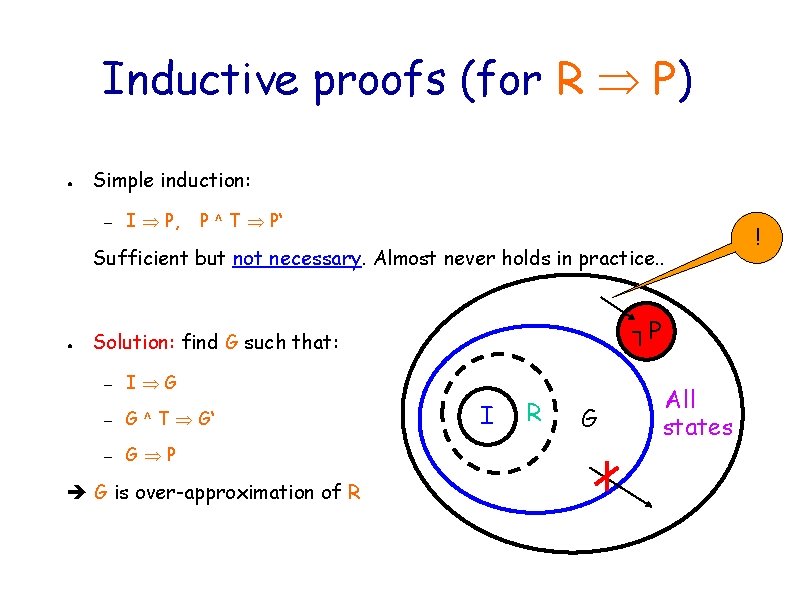
Inductive proofs (for R P) ● Simple induction: – I P, P ^ T P‘ Sufficient but not necessary. Almost never holds in practice. . ● ┐P Solution: find G such that: – I G – G ^ T G‘ – G P G is over-approximation of R I R G All states !

ic 3 - basic properties ● Complete – always terminates with correct result ● SAT based, no unrolling ● If P is invariant, produces a CNF formula G, s. t. : – ● I G – G ^ T G’ – G P ┐P I R G All states If not, produces a (generalized) CEX α 0, α 1, …, αk s. t. : – all α 0 states belong to I – all αi states lead to some αi+1 state – αk is in ┐P I a 0 a 1 … ┐P ak

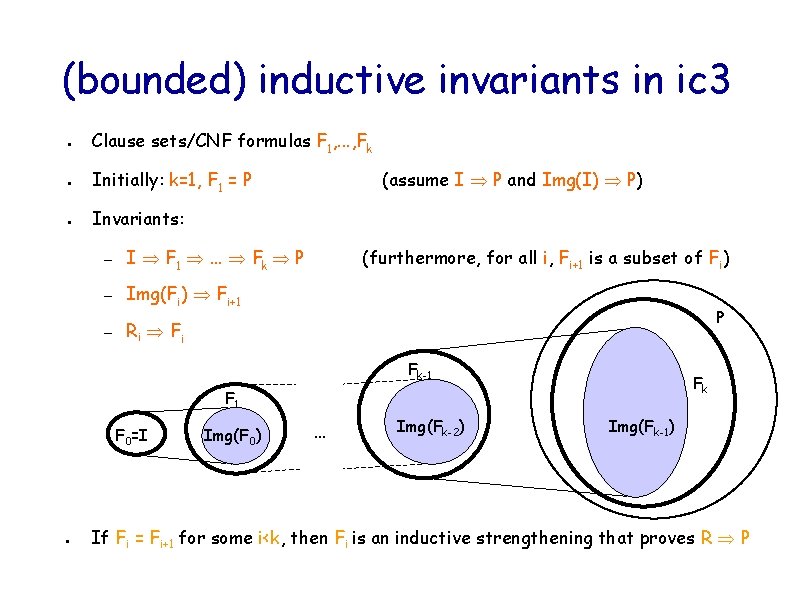
(bounded) inductive invariants in ic 3 ● Clause sets/CNF formulas F 1, . . . , Fk ● Initially: k=1, F 1 = P ● (assume I P and Img(I) P) Invariants: – I F 1 . . . Fk P – Img(Fi) Fi+1 – (furthermore, for all i, Fi+1 is a subset of Fi) P Ri F i Fk-1 Fk F 1 F 0=I ● Img(F 0) … Img(Fk-2) Img(Fk-1) If Fi = Fi+1 for some i<k, then Fi is an inductive strengthening that proves R P

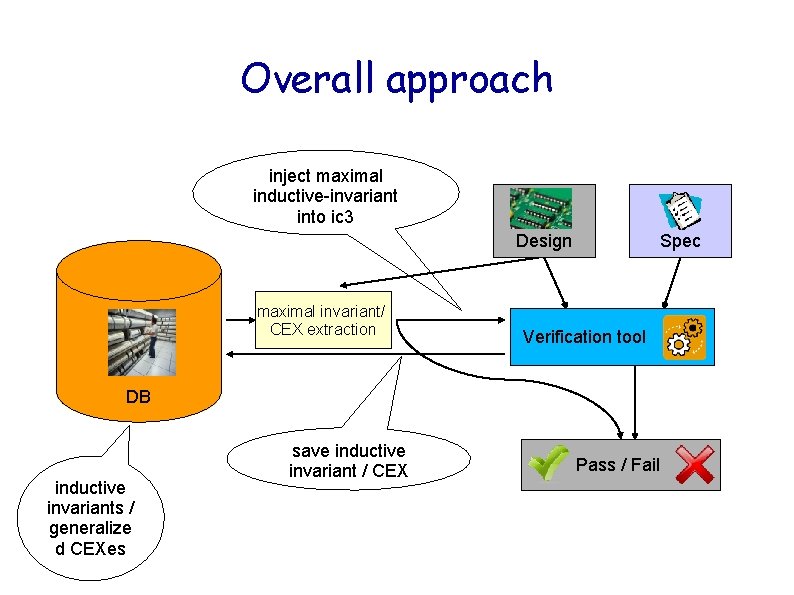
ic 3 progress and termination ● ● ● Inductive clauses that block “bad state predecessors” are added to the sets Fi, in a way that maintains the containment invariants Once in a while, clauses are “pushed” to higher Fi’s ic 3 terminates when either: – Fi=Fi+1 for some i we save the inductive invariant Fi – it finds a CEX: chain of bad state predecessors that starts at I we generalize and save the CEX + we save the absolute invariants * Absolute inductive invariants are those clauses that were “pushed” beyond Fk

How to reuse saved invariants? Finding maximal inductive invariant ● Input: I, T, P and C = {c 1, …, cm} - candidate invariant clauses ● Output: PASS or maximum subset Q of C such that I Q and Q ^ T Q‘ * Note: if Q 1 ^ T Q’ 1 and Q 2 ^ T Q‘ 2 then (Q 1 U Q 2) ^ T (Q’ 1 U Q’ 2) • Once such Q is found, we can “inject” it into ic 3 by conjoining Q with all sets Fi • This saves ic 3 the effort of “rediscovering” the invariants from Q

Finding Q using a SAT solver * that supports Solve. With. Assumptions(a 1, . . . , ak) 1. cnfize T and I, set Q: =C 2. remove from Q all clauses that are not implied by I 3. for every ci in Q, introduce two auxiliary vars: xi and y’i 4. for every i, cnfize xi ci and y’i ┐c’i 5. Solve. With. Assumptions(x 1, . . . , x|Q|, (y’ 1 v. . . v y’|Q|)) 6. if unsat: if sat: Q is invariant remove from Q each ci with assign(y’i)=1 and goto 5 7. if Q P output PASS, ow return Q

Overall approach inject maximal inductive-invariant into ic 3 Design maximal invariant/ CEX extraction Spec Verification tool DB inductive invariants / generalize d CEXes save inductive invariant / CEX Pass / Fail

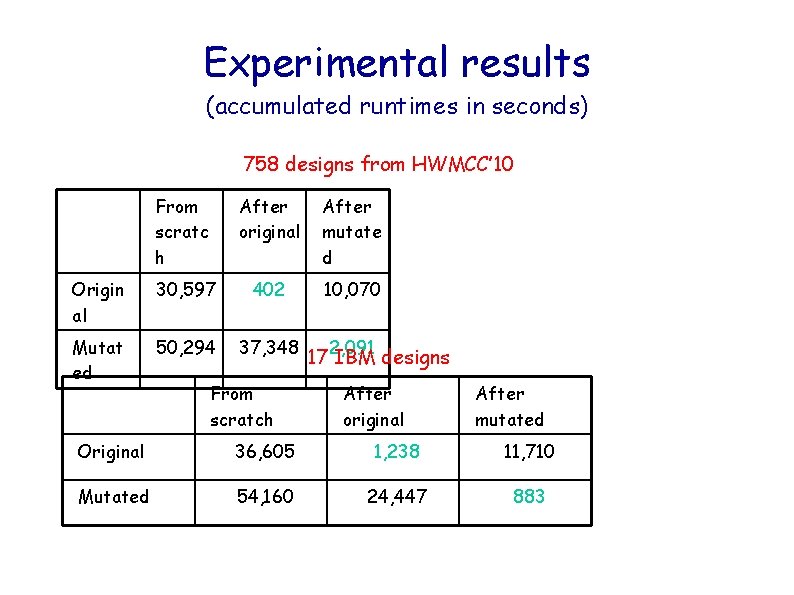
Experimental results (accumulated runtimes in seconds) 758 designs from HWMCC’ 10 From scratc h After original After mutate d Origin al 30, 597 402 10, 070 Mutat ed 50, 294 37, 348 From scratch 17 2, 091 IBM designs After original After mutated Original 36, 605 1, 238 11, 710 Mutated 54, 160 24, 447 883

Concluding remarks ● ● ● ic 3 can be used to save small inductive proofs, and generalized CEXes the technique is robust since ic 3 invariants and CEXes involve only state variables makes coverage and regression verification almost immediate parts from inductive proofs can be used even if design/spec has significantly changed saved information is reusable even when verification result changes

The End

Generalizing assignments ● Input: circuit C and assignment a such that C(a)=y ● Output: partial assignment a’ such that C(b)=y for all extensions b of a’ * a’ is obtained by subst. some of the 0, 1 values in a with x (don’t cares) Standard algs: • start from root and propagate “cares” • start from leaves and propagate “don’t cares”

Generalizing assigns. with solver ● Input: circuit C and assignment a such that C(a)=y ● Output: partial assignment a’ such that C(b)=y for all extensions b of a’ 1. cnfize C 2. Solve. With. Assumptions(┐(C(a)=y), a 1, . . . , an) * must return unsat (BCP) 3. if ai participates in the conflict set a’i = ai else set a’i = x

Generalizing assigns. with solver 1. cnfize C 2. Solve. With. Assumptions(┐(C(a)=y), a 1, . . . , an) * must return unsat (BCP) 3. if ai participates in the conflict set a’i = ai else set a’i = x Advantages: 1. easy to enforce additional constraints (e. g. learnt clauses and invars) 2. can order the variables in the assumptions acc. to some priority 3. can run after standard algs 4. no real solving – just BCP 5. shrinks by additional 30 -40% after ternary simulation (like in PDR)