I Observations exprimentales 1 En lumire monochromatique Lumire

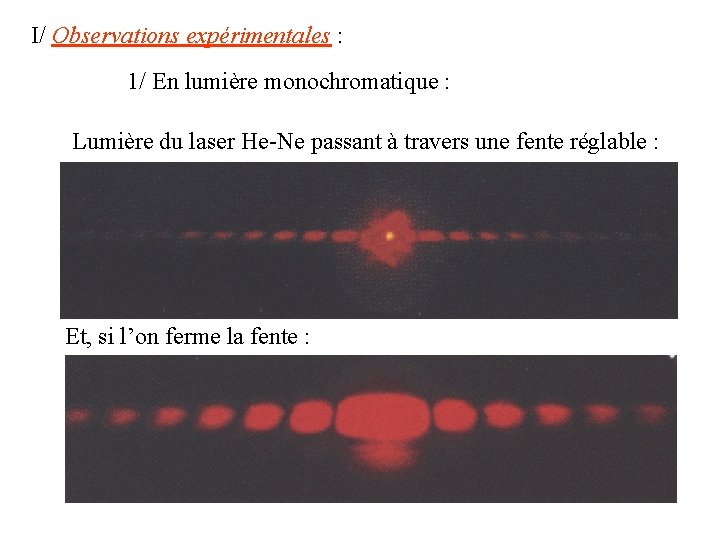
I/ Observations expérimentales : 1/ En lumière monochromatique : Lumière du laser He-Ne passant à travers une fente réglable : Et, si l’on ferme la fente :

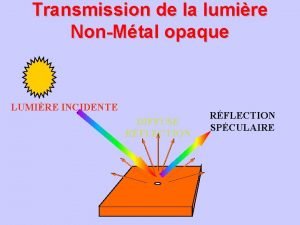
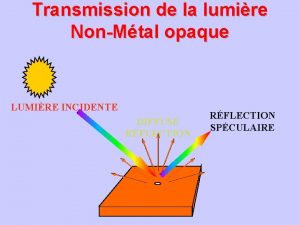
I/ Observations expérimentales : 1/ En lumière monochromatique : Lumière du laser He-Ne passant à travers une ouverture circulaire :

I/ Observations expérimentales : 2/ En lumière blanche : Lorsque la fente est suffisamment petite on observe :
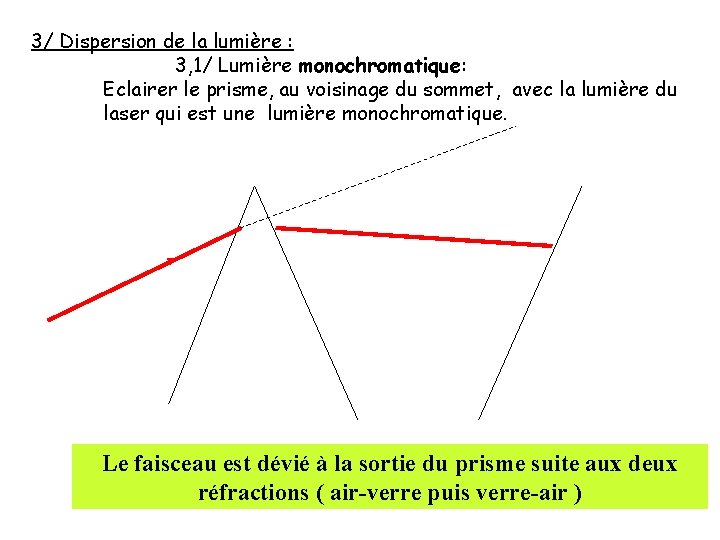
3/ Dispersion de la lumière : 3, 1/ Lumière monochromatique: Eclairer le prisme, au voisinage du sommet, avec la lumière du laser qui est une lumière monochromatique. Le faisceau est dévié à la sortie du prisme suite aux deux réfractions ( air-verre puis verre-air )
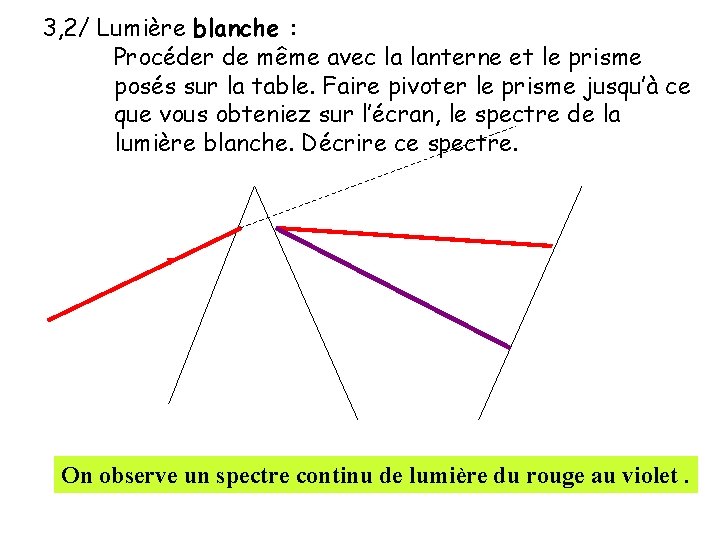
3, 2/ Lumière blanche : Procéder de même avec la lanterne et le prisme posés sur la table. Faire pivoter le prisme jusqu’à ce que vous obteniez sur l’écran, le spectre de la lumière blanche. Décrire ce spectre. On observe un spectre continu de lumière du rouge au violet.

II/ Modèle ondulatoire de la lumière: 1/ La lumière est une onde: La lumière qu’il s’agisse d’une lumière monochromatique, ou de lumière polychromatique est diffractée. Elle peut donc être décrite comme une onde. Il s’agit d’une onde électromagnétique car la perturbation qui se propage modifie les champs magnétique et électrique perpendiculairement au sens de propagation. Le phénomène de diffraction est d’autant plus important que les dimensions de l’objet diffractant sont faibles. La figure de diffraction est orthogonale à la dimension longitudinale de l’objet diffractant. Les dimensions de la fente ou de l’objet responsable de cette diffraction sont de l’ordre de grandeur de la longueur d’onde de la lumière utilisée.

2/ La lumière se propage dans le vide : Contrairement aux ondes mécaniques qui nécessitent un milieu matériel, la lumière se propage dans le vide. On peut recevoir sur Terre la lumière des étoiles ayant traversé le vide intersidéral. La célérité de la lumière dans le vide est voisine de 3. 108 m. s-1 Quelle que soit la fréquence de l’onde. Sa valeur exacte est c = 299 792 458 m. s-1, elle a été fixée à cette valeur par une convention internationale c’est une constante fondamentale du système international d’unités. Elle sert depuis à la définition du mètre ( 1983 ) : le mètre m est la distance parcourue dans le vide par la lumière en 1/299 792 458 s. La lumière se propage aussi dans les milieux transparents.

3/ Longueurs d’onde dans le vide: Soit une lumière monochromatique (par exemple la lumière du laser que l’on peut considérer comme monochromatique) ; elle peut être représentée par une onde progressive sinusoïdale de fréquence n. La longueur d’onde dans le vide est donnée par la relation : l 0 = c. T = c/n * l 0 se mesure en mètres (nm dans le cas de la lumière) ; c en m. s -1 ; n en hertz (Hz) Exemple : le laser He-Ne émet une lumière monochromatique de longueur d’onde l 0 = 632, 8 nm. Il lui correspond une fréquence n telle que n = c / l 0 = 299792458 /632, 8. 10 -9 = 4, 738. 1014 Hz. Cas d’une lumière polychromatique : l’œil humain peut percevoir une infinité de radiations monochromatiques dont les fréquences sont comprises grossièrement entre 7, 5. 1014 Hz et 3, 7. 1014 Hz. Les couleurs correspondantes s’étalent entre le rouge foncé (l 0 800 nm) et le violet (l 0 400 nm). D’autres ondes électromagnétiques se propagent à la manière de la lumière, mais ne sont pas perceptibles à l’œil: Infrarouge, Ultraviolet, Ondes radio (hertziennes), micro-ondes, rayons X, etc. . . (voir livre Doc 15 page 53).

4/ Propagation de la lumière dans les milieux transparents et dispersion de la lumière : 4. 1 Invariance de la fréquence. La fréquence d’une onde électromagnétique est imposée par la source. Elle ne dépend pas du milieu de propagation et ne varie donc pas lors d’un changement de milieu.

4. 2 Indice d’un milieu et vitesse de propagation. La célérité v d’une onde lumineuse dépend du milieu dans lequel elle se propage. Définition : l’indice de réfraction n d’un milieu transparent est donné par la relation : n = c / v. La célérité de la lumière dans le vide étant la plus grande vitesse possible, il en résulte que n 1. Remarque : n est un nombre sans dimension. Quelques exemples : n air 1, 0 ; n eau 1, 3 ; n verre ordinaire 1, 5 ; n diamant 2, 4 ….

4. 3 Indice et longueur d’onde. Dans le vide, une radiation de fréquence n a une longueur d’onde l 0 telle que l 0 = c / n. Dans un milieu transparent d’indice n on a : n = c / v et l = v / n. On peut donc écrire : l= ? La longueur d’onde d’une radiation de fréquence donnée dépend du milieu de propagation.

4. 4 Dispersion de la lumière. La lumière blanche est décomposée par un prisme donc la déviation dépend de la couleur et donc de la fréquence. En appliquant la seconde loi de Descartes pour la réfraction, on peut écrire : nair sin i = nverre sin r. Le premier terme étant constant et r variant pour chaque radiation colorée, on peut en déduire que l’indice de réfraction du verre dépend de la “ couleur ” et donc de la fréquence de la radiation qui le traverse. On montre que lorsque n diminue, n diminue aussi. Sachant que v = c / n et que n dépend de la fréquence de l’onde, on peut conclure que v dépend de la fréquence de la radiation. Les milieux transparents, autres que l’air, sont dispersifs. C’est cette propriété qui permet d’obtenir des spectres de lumières polychromatiques.
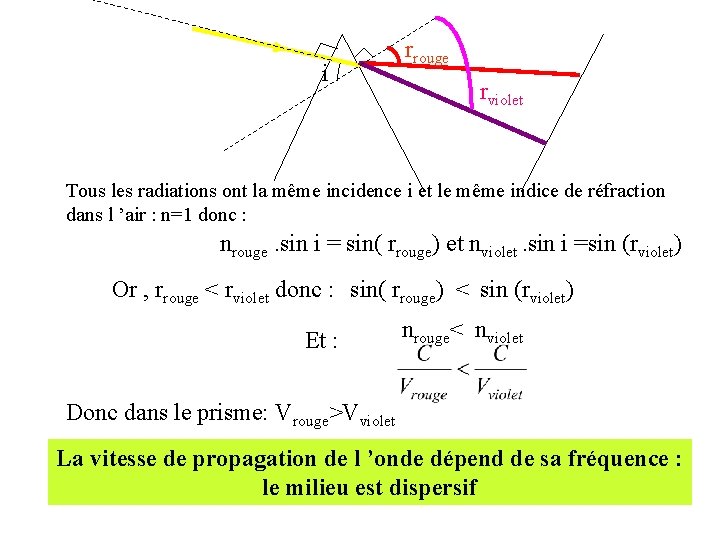
i rrouge rviolet Tous les radiations ont la même incidence i et le même indice de réfraction dans l ’air : n=1 donc : nrouge. sin i = sin( rrouge) et nviolet. sin i =sin (rviolet) Or , rrouge < rviolet donc : sin( rrouge) < sin (rviolet) Et : nrouge< nviolet Donc dans le prisme: Vrouge>Vviolet La vitesse de propagation de l ’onde dépend de sa fréquence : le milieu est dispersif

5/ Diffraction de la lumière : Nous avons mis en évidence expérimentalement une relation simple entre la longueur d’onde l 0 la largeur de l’objet diffractant et la largeur de la figure de diffraction : q (radians) = l 0 (m) a(m) Le phénomène de diffraction est d’autant plus important que la taille de l’objet diffractant est petite.

- Slides: 16