Graphs of Motion Physics Notes Introduction to Graphs
















- Slides: 22

Graphs of Motion Physics Notes

Introduction to Graphs are mathematical pictures. They are the best way to convey a description of real world events in a compact form. Graphs of motion come in several types depending upon which of the kinematic quantities (time, displacement, velociy, or acceleration) are assigned to which axis.

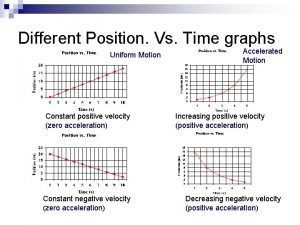
Displacement/Time Slope equals velocity. The “y” intercept equals the initial displacement. When two curves coincide, the two objects have the same displacement at that time.

Displacement/time

Displacement/time Straight lines imply constant velocity. Curved lines imply acceleration. An object undergoing constant acceleration traces a portion of a parabola. Average velocity is the slope of the straight line connecting the endpoints of a curve.

Displacement/time When the slope is negative, the object is traveling in the negative direction. Positive slope implies motion in the positive direction. Negative slope implies motion in the negative direction. Zero slope implies a state of rest.

Displacement/time

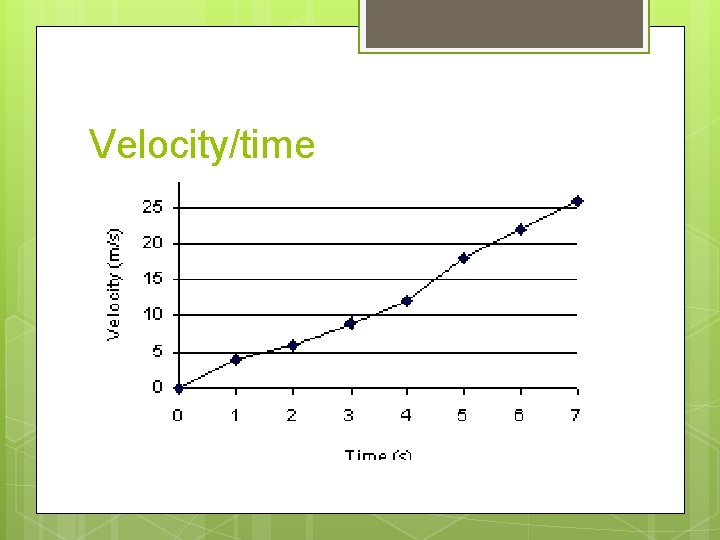
Velocity/time Not the same as displacement/time graphs. In a velocity/time graph, higher means faster not farther. Slope equals acceleration. The “y” intercept equals the initial velocity. When two curves coincide, the two objects have the same velocity at that time.

Velocity/time Straight lines imply uniform acceleration. Curved lines imply non-uniform acceleration. An object undergoing constant acceleration traces a straight line.

Velocity/time

Velocity/time Since a curved line has no single slope, we must decide what we mean when we asked for the acceleration of an object. If the average acceleration is desired, draw a line connecting the endpoints of the curve and calculate slope. If the instantaneous acceleration is desired, take the limit of this slope as the time interval shrinks to zero, that means take the slope of a tangent to a curve at any point.

Velocity/time

Velocity/time Positive slope implies an increase in velocity in the positive direction. Negative slope implies an increase in velocity in the negative direction. Zero slope implies motion with constant velocity.

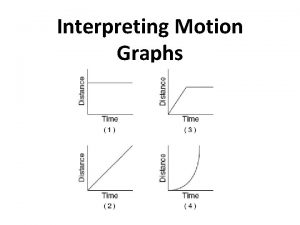
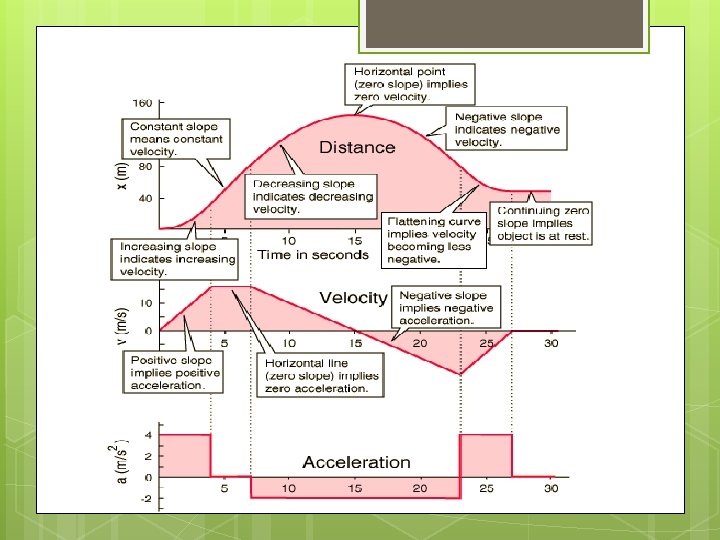
How to determine displacement, velocity, and acceleration? Given a graph of any of these quantities (displacement, velocity, or acceleration), it is always possible in principle to determine the other two.

How to determine displacement, velocity, and acceleration from a graph? When acceleration is constant, the average velocity is just the average of the initial and final values in an interval. To find the displacement of the object during a specific interval, simply find the area under each segment of the line. See example on next slide.


Fundamentals of physics The first derivative of displacement with respect to time is velocity. The derivative of a function is the slope of a line tangent to its curve at a given point. The inverse operation of the derivative is called the integral

Fundamentals of physics The integral of a function is the cumulative area between the curve and the horizontal axis over some interval. This inverse relation between the actions of derivative (slope) and integral (area) it is called the fundamental theorem of calculus.

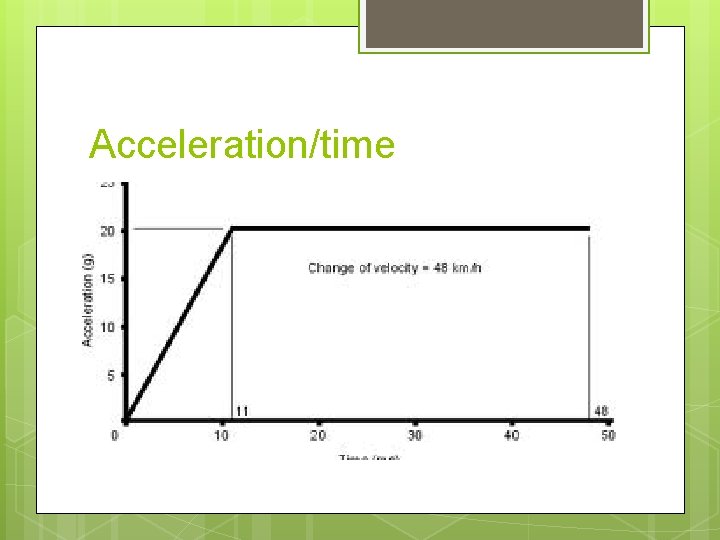
Acceleration/time graphs of objects that have a constant velocity will be a horizontal line collinear with a horizontal axis. On this type of graph…slope is meaningless. The “y” intercept equals the initial acceleration.

Acceleration/time When two curves coincide, the two objects have the same acceleration at that time. An object undergoing constant acceleration traces a horizontal line. Zero slope implies motion with constant acceleration. Acceleration is the rate of change of velocity with time.

Acceleration/time

Acceleration/time Transforming a velocity/time graph to acceleration/time graph means calculating the slope of a line tangent to the curve at any point (this is called finding the derivative). The reverse process involves calculating the cumulative area under the curve (finding the integral). The area under the curve equals the change in velocity.
 Waves physics notes
Waves physics notes Scanything
Scanything State testing and testability tips
State testing and testability tips Speed and velocity
Speed and velocity Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Polynomial end behavior chart
Polynomial end behavior chart Hooke's law notes
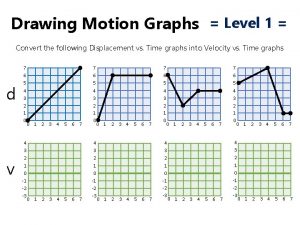
Hooke's law notes Drawing motion graphs
Drawing motion graphs Motion graphs warm up answer key
Motion graphs warm up answer key Motion graph story book project
Motion graph story book project Interpret the graph below
Interpret the graph below Always-on
Always-on Http //camillasenior.homestead.com/motion graphs.pdf
Http //camillasenior.homestead.com/motion graphs.pdf Tvtat
Tvtat Kinematics motion in one dimension
Kinematics motion in one dimension Cube wisc
Cube wisc Physics 111 lecture notes
Physics 111 lecture notes Conceptual physics chapter 8
Conceptual physics chapter 8 Physics 101 lecture
Physics 101 lecture Conceptual physics chapter 4
Conceptual physics chapter 4 Physics 101 lecture notes pdf
Physics 101 lecture notes pdf Ap physics 2 notes
Ap physics 2 notes Advanced higher physics formula sheet
Advanced higher physics formula sheet