GRAFOS ALGORITMOS FUNDAMENTALES ESTRUCTURAS DE DATOS MATRIZ DE

GRAFOS: ALGORITMOS FUNDAMENTALES ESTRUCTURAS DE DATOS

MATRIZ DE CAMINOS � Es una matriz cuadrada P, � Que representa si hay o no camino � Entre dos vertices Vi y Vj

CIERRE TRANSITIVO � Es el grafo resultante de la matriz de caminos � Si un grafo es fuertemente conexo �Su cierre transitivo es un grafo completo

UN POSIBLE ALGORITMO � � Entre Vi y Vj puede haber camino � Directo, cuando A[i][j] == 1, camino de long. 1 � O pasando por otros vertices Si solo analizamos pasar por un Vk extra � Cuando A[i][k] == 1 && A[k][j] == 1, Long. 2 � Si Vk puede ser V 1 o V 2 o … Vn, realmente (A[i][1] && A[1][j]) || (A[i][2] && A[2][j]) || (A[i][n] && A[3][n]) � Que representa A * A, A 2 � � Nos indica solo si hay un camino de long. 2 entre Vi y Vj La matriz de caminos indicara si hay camino ya sea � De long. 1 o de long. 2 o de long. 3 o de long. N, es decir: B = A + A 2 + A 3 + A 4 +…. An

WARSHALL: MAS EFICIENTE � El anterior algoritmo � Es poco eficiente, peor � Cuando el grafo tiene muchos vertices � Warshall propuso otro algoritmo � Mas eficiente � Calcular una secuencia de matrices cuadradas � De 0 s(no hay camino) y 1 s(hay camino) � P 0, P 1, P 2, P 3… PN � La diferencia entre Pk y Pk-1 � Se basa añadir un vertice Vk-1 al analisis � Para saber y a traves de Vk-1 hay camino entre V 1 y Vj

COMO FUNCIONA � Existe una matriz inicial P 0 � � Inidica si hay o no camino DIRECTO de Vi a Vj La matriz que le sigue P 1 Indicaria si hay o no camino DIRECTO (Esto ya lo sabe P 0) � O pasando por V 0 (añade este vertice al analisis) � � P 2 Indicaria si hay camino DIRECTO o pasando por V 0 (Esto ya lo sabe P 1) � O pasando por V 1 � � P 3 Indicaria si hay camino DIRECTO o pasando por V 0, o V 1 (Lo sabe P 2) � O pasando por V 2 � � Pk Indicaria lo que ya sabe Pk-1 � O pasando por Vk-1 �

EL ALGORITMO ENTONCES � Debemos encontrar Pn � Sabiendo que Pk[i][j] es 1 si � Pk-1[i][j] es 1 o � Pk-1[i][k] && Pk-1[k][j] � En otras palabras:

WARSHALL IMPLEMENTADO Matriz. Ady Warshall(Grafo G){ int i, j, k; Matriz. Ady P; Copiar. Matrices(P, G. A); for(k = 0; k < G. nvertices; k++){ for(i = 0; i < G. nvertices; i++){ for(j = 0; j < G. nvertices; i++){ P[i][j]= P[i][j] || (P[i][k] && P[k][j]); } } }return P; }

CAMINOS MAS CORTOS � Frecuentemente, se desea conocer � Cual es el camino mas corto � Entre � En en una red un par de vertices este caso � Si importa cuantos caminos existen � Si ya conozco un camino, pero encuentro uno mejor, sustituir � Se aplica el algoritmo de Dijkstra � Es un algoritmo avido, ya que � Resuelve el problema en sucesivos pasos � En cada paso � Selecciona la solucion mas optima

DIJKSTRA � Dado � Las � Al un V 0, Dijkstra busca un conjunto D con menores distancias de V 0 al resto de vertices inicio, solo conocemos � Las distancias de los adyacentes � D es inicializada a � Factor de peso para los adyacentes, Infinito para los no adyacentes �D va ser mejorado sucesivamente � Escogiendo � Que tenga la distancia mas corta V 0, Vk � Probamos � Se el vertice Vk no elegido antes si pasando por Vk puede obtener distancias mas cortas de las que tenemos � Para cada Vertice restante del grafo

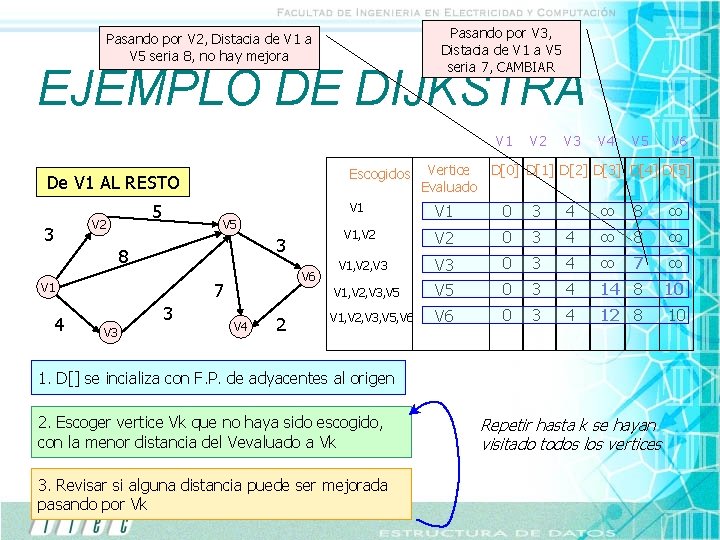
Pasando por V 3, Distacia de V 1 a V 5 seria 7, CAMBIAR Pasando por V 2, Distacia de V 1 a V 5 seria 8, no hay mejora EJEMPLO DE DIJKSTRA V 1 Escogidos De V 1 AL RESTO 5 V 2 3 V 5 3 8 V 6 7 V 1 4 3 V 3 2 V 3 V 4 V 5 V 6 D[0] D[1] D[2] D[3] D[4] D[5] V 1 0 3 4 ∞ 8 ∞ V 1, V 2, V 3 0 3 4 ∞ 7 ∞ V 5 0 3 4 14 8 10 V 6 0 3 4 12 8 10 V 1, V 2, V 3, V 5 V 4 Vertice Evaluado V 2 V 1, V 2, V 3, V 5, V 6 1. D[] se incializa con F. P. de adyacentes al origen 2. Escoger vertice Vk que no haya sido escogido, con la menor distancia del Vevaluado a Vk 3. Revisar si alguna distancia puede ser mejorada pasando por Vk Repetir hasta k se hayan visitado todos los vertices

DIKSTRA 1. Se crea una lista de VDiks con todos los vertices del grafo, y cada VDiks creado tambien se encola 2. Se saca de la cola el menor VDiks por distancia(vmenor) 3. Por cada VDiks v de la lista, se revisa Si su vertice es adyacente al vertice de vmenor y si pasando por vmenor se puede conseguir una mejor distancia Si es asi, se modifica v con los nuevos datos 4. Se repite todo desde el paso 2 hasta que no haya nada mas en la cola

CAMINOS MAS CORTOS ENTRE TODOS LOS PARES DE VERTICES � Es una generalizacion de lo anterior � Si se puede obtener la menor distancia � � De un V 0 al resto Tambien se puede obtener La menor distancia de todos los vertices � Al resto � � Se podria aplicar Dijkstra A cada vertice � Y obtener n vectores D, o , una matriz F � � Pero se puede aplicar otro algoritmo

FLOYD � Este � Se algoritmo se basa en Warshall calculaba una secuencia de matrices Pk � Cada Pk evaluaba dos opciones � Que Pk-1 indicara camino entre Vi y Vj o � Que Pk-1 indicara camino entre Vi y Vj � Pasando � Floyd por Vk tambien calcula Fk, pero � Cada Fk escogera la menor distancia entre � Distancia entre Vi y Vj, indicado por Fk-1 o � Distancia entre Vi y Vj pasando por Vk, indicado por Fk-1

ARBOL DE EXPANSION DE COSTE MINIMO � Dado un grafo G �No dirigido �Valorado, con pesos no negativos � El arbol de expansion minima �Es un grafo parcial conexo a partir de G �Tal que la suma de sus aristas sea minima � Ejemplo �Redes de aplicacion de comunicaciones, de costo minimo

ALGORITMO DE PRIM � Dado � Un el grafo, se debe seleccionar vertice de inicio v � Dicho vertice v se añade a un conjunto W � Escoger el vertice u que no pertenezca a. W � Adyacente a cualquiera de los vertices de W � Y que tenga un costo minimo � Añadir el vertice u al conjunto W � Repetir proceso hasta que V == W

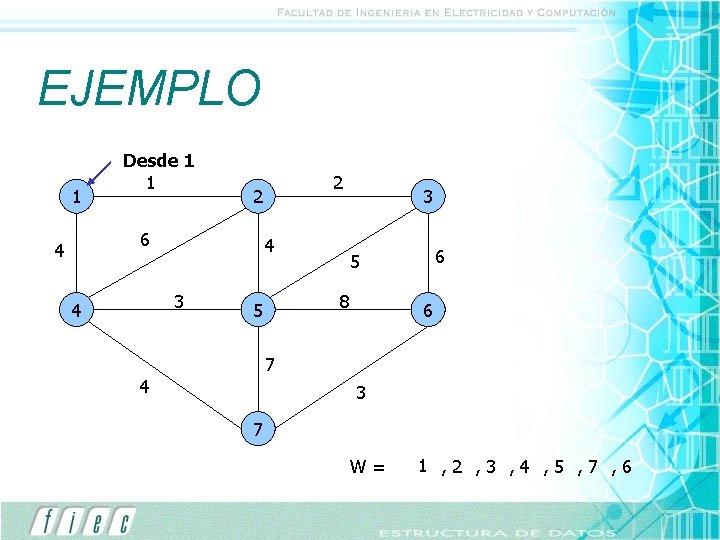
EJEMPLO 1 Desde 1 1 6 4 4 3 4 2 2 3 8 5 6 7 4 3 7 W= 1 , 2 , 3 , 4 , 5 , 7 , 6

PRIM 1. Se crea un grafo nuevo con los mismos vertices del grafo original 2. vorigen se marca como visitado 3. Los arcos de vorigen, cuyos vertices destino no han sido visitados, se encolan por peso 4. Se desencola el menor en peso de los arcos no visitados(amenor) y su vertice destino se marca como visitado 5. En el nuevo grafo, se lanza el arco correspondiente a amenor(de ida y vuelta) 6. Se repite todo desde el punto 3 pero para un vorigen igual al vertice del arco sacado(amenor) hasta que el numero de vertices marcados como visitados sea igual al numero de vertices del grafo

ALGORITMO DE KRUSKAL � Kruskal se basa en el concepto de � Componentes � Sabemos � Deben � Lo que en el arbol de expansion aparecer todos los vertices de G que no sabemos aun � Es � Lo conexas que arcos escoger para unirlos que a Kruskal le interesara elegir � Son los arcos, no los vertices, como en Prim

COMO FUNCIONA � Primero � Estos � Luego añadir todos los vertices al arbol A forman n componentes conexas elegir el arco de costo minimo � Que no haya sido elegido anteriormente y que � No una dos vertices de una misma componente � Este � Se proceso se repite hasta que hayan unido todos los vertices � Es decir, n-1 veces

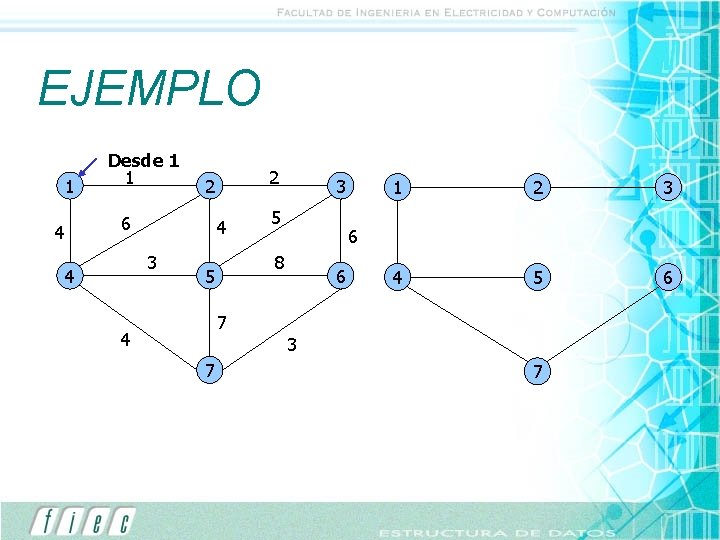
EJEMPLO 1 4 Desde 1 1 6 4 3 4 2 2 3 5 2 3 4 5 6 6 8 5 1 6 7 4 3 7 7