F 4 6 Statistikens grunder 15 p dagtid

F 4 -6 Statistikens grunder, 15 p dagtid HT 2012 Föreläsningar F 4 -F 6

Repe titio Tolkning av sannolikhet Frekventistisk n. A /n → P(A) då n → ∞ Klassisk antal(A) / antal(Ω) = P(A) storlek(A) / storlek(Ω) = P(A) Subjektiv (personlig) insats/total vinst = P(A) n

Repe titio Lite mängdlära n • Låt e 1, e 2, osv. beteckna element • Låt A, B beteckna mängder av element – Klamrar brukar användas {∙} – Ex. A = {1, 2} • Om ei tillhör A skriver vi ei ∈ A – Ex. 1 ∈ {1, 2} • Om A är en delmängd av B skriver vi A ⊆ B – Ex. A = {1, 2} ⊂ B = {1, 2, 3, 4, 5, 6} – Strikt delmängd betecknas ⊂ – Delmängd betecknas ⊆

Repe titio Lite mängdlära, forts. Antag att Ω = {1, 2, 3, 4, 5, 6} och att A = {1, 2}, B = {2, 3, 4} och C = {3} • Komplementet till en mängd är allt som inte ingår i mängden och betecknas med Ā eller A’ – Ex. Ā = {3, 4, 5, 6} • Unionen av mängder betecknas med ∪ – Ex. A ∪ B = {1, 2, 3, 4} • Snittet av mängder betecknas med ∩ – Ex. A ∩ B = {2} n

Repe titio Lite mängdlära, forts. • Tomma mängden är delmängden till Ω som inte innehåller några element alls. Betecknas med ∅. • Två mängder är disjunkta (oförenliga) om snittet är tomt – Ex. A = {1, 2} och C = {3} A∩B=∅ n

Övning Ett kort dras slumpmässigt ur en kortlek bestående av de vanliga 52 korten. Deiniera händelserna • A = ”rött kort, • B = ”kung” • C = ”spader” (a) Vilka par av A, B och C är disjunkta? (b) Tolka följande händelser och rita Venndiagram: i. Ā ii. A ∩ B iii. A ∩ C iv. A ∪ B v. A ∪ C vi. (A ∪ C)

Repe titio En axiomatisk teori Kolmogorovs axiom: En sannolikhet är en funktion P som tilldelar varje möjlig händelse A i ett utfallsrum Ω ett tal P (A) , så att följande villkor är uppfyllda: • P(A) ≥ 0 • P(Ω) = 1 • Om A 1, A 2, . . . , Ak, är parvis disjunkta händelser i S, då är P(A 1 ∪ A 2 ∪. . . ∪ Ak) = P(A 1) + P(A 2) +. . . + P(Ak) n

Repe titio n En axiomatisk teori, forts. • Samtliga tre synsätt (definitioner) på vad en sannolikhet egentligen är, är förenliga med Kolmogorovs axiom. – Kom ihåg att vi har en formell definition på vad en sannolikhet är också • Massor av nya påståenden kan nu härledas ur dessa tre axiom – dvs. bevisas vara sanna inom det generella formella systemet

Repe titio n En axiomatisk teori, forts. • P(Ā) = 1 - P(A) • P(∅) = 0 • Om A ⊂ B så gäller P(A) ≤ P(B) • P(A) ≤ P(Ω) = 1 • P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

F 4 Matematikrep • Summatecknet • Potensräkning • Logaritmer • Kombinatorik

Summatecken Säg att vi har n stycken tal x 1, …, xn Summan av dessa tal (alltså x 1 + … + xn) skrivs kortfattat med hjälp av summatecken: ”summa xi då i går fr. o. m. 1 t. o. m. n ”

Summatecken, forts. Vad betyder följande? • • •

Summatecken, forts. Ex. Antag att x 1 = 3, x 2 = -2, x 3 = 5, x 4 = 3 Beräkna: Medelvärde: Varians: Standardavvikelse:

Ny Summatecken, forts. Övning: Utveckla (dvs. lista termerna) 1. 2. 3.

Potensräkning b ggr • ab = a∙a∙ … ∙a • ab∙ac = a(b+c) • (ab)c = a(bc) • a–b = 1 / ab • a 0 = 1 • a 1/b =

En komboövning Beräkna följande för n = 0, 1, 2, 3 Svar: n = 0; n = 1; n = 2; n = 3; 20 = 1 20 + 21 = 1 + 2 = 3 20 + 21 + 22 = 1 + 2 + 4 = 7 20 + 21 + 22 + 23 = 15

Logaritmer Obs! a, b > 0 och a ≠ 1 Antag att vi har följande: ab = c Vi vet a och c och söker b b = loga c Ex. Det tal som vi upphöjer a till för att få c 10 x = 10000 x = log 1010000 = log 10000 = lg 10000 = 4 Några olika beteck- ningar för 10 -logaritm Ex. ex = 80 x = ln 80 = 4, 3820266…. . Naturliga logaritm

Logaritmer, forts. e = basen för den naturliga logaritmen = 2, 71828…. . Räkneregler: Obs! x, y > 0 • ln(x∙y) = lnx + lny • ln(x/y) = lnx – lny • ln xk = k∙lnx • ln 1 = 0 • elnx = x • ln e = 1 • ln(ex) = x

Ny Logaritmer, forts. Ex. Bevisa första räkneregeln: Vi definierar a, b och c 1. ea = x ⟹ a = ln x 2. eb = y ⟹ b = ln y 3. ec = (x∙y) ⟹ c = ln(x∙y) enl. definitionen av logaritmfunktionen. Vi har alltså Enligt regeln • x∙y = ea∙eb = ea+b för potenser ⟹ ln(x∙y) = a + b = ln x + ln y Enligt definitionen för logaritmfunktionen Enligt definitionen ovan

Logaritmer, forts. Övningar: • ln 12 = ln 3 + ln 4 • ln 0, 25 = ln(1/4) = ln 1 – ln 4 = – ln 4 • ln 64 = ln 26 = 6∙ln 2 • ln(32/9) = ln 32 – ln 9 = ln 25 – ln 32 = 5 ln 2 – 2 ln 3

Kombinatorik Att räkna ut hur många sätt något kan göras. Ex. Matsedel med tre förrätter, fyra huvudrätter och två efterrätter. På hur många olika sätt kan en trerätters måltid komponeras? Svar: Illustration: Träddiagram

Kombinatorik, forts. Multiplikationsprincipen • Ett experiment har m 1 möjliga utfall • Ett annat efterföljande experiment har m 2 möjliga utfall • Vi gör först det ena sedan det andra experimentet • Totalt finns det m 1 × m 2 möjliga utfall.

Kombinatorik, forts. Exempel Påse med numrerade kulor 1, …, n • Vi drar en kula slumpmässigt och noterar dess nummer Hur många möjliga utfall? • Vi drar en kula till slumpmässigt och noterar dess nummer Hur många möjliga utfall?

Kombinatorik, forts. Exempel, forts Samma påse med kulor 1, …, n • Vi har den totala händelsen (kula 1’s nummer, kula 2’s nummer) • Hur många möjliga utfall? • Utan återläggning: • Med återläggning:

Kombinatorik, forts. Exempel, forts • Spelar ordningen någon roll? • Dvs. skiljer vi t. ex. på (1, 3) och (3, 1) eller betraktar vi det som samma sak? Två fall som uppstår: • Ordningen spelar roll • Ordningen spelar ingen roll

Kombinatorik, forts. Permutationer • Ett arrangemang av n olika objekt i en bestämd ordning kallas för en permutation av objekten. • Hur många olika permutationer kan man bilda av n olika objekt? • Antalet olika permutationer av n olika objekt är: n! = 1 × 2 × 3 × … × (n-1) × n • n-fakultet; (eng. n factorial)

Kombinatorik, forts. Permutationer Ex. På hur många olika sätt kan vi permutera de tre objekten A, B, C? Svar: 3! = 1× 2× 3 = 6 olika sätt, nämligen ABC, ACB, BAC, BCA, CAB, CBA. OBS! Vi definierar 0! = 1

Kombinatorik, forts. • Dragning utan återläggning – Vi drar en kula slumpmässigt och noterar dess nummer och lägger inte tillbaks den inför nästa dragning – Vi kan bara få ett nummer en gång • Dragning med återläggning – Vi drar en kula slumpmässigt och noterar dess nummer och lägger tillbaks den inför nästa dragning – Vi kan dra samma nummer flera gånger i en sekvens av dragningar

Kombinatorik, forts. • På hur många sätt kan vi välja ut k objekt från n objekt (k ≤ n), ifall vi bryr oss om ordningen? Och utan återläggning? • Svar: Ex. n = 5, k = 2

Kombinatorik, forts. Kombinationer • På hur många sätt kan vi välja ut k objekt från n objekt (k ≤ n), ifall vi inte bryr oss om ordningen? Utan återläggning? • Svar: • ”n över k”, binomialkoefficient • Obs! Vi definierar

F 5 Sannolikheter • Framförallt Nyquist Kap 5 • Men först lite repetition och lite mer kombinatorik

Repe titio Kombinatorik, forts. Multiplikationsprincipen • Ett experiment har m 1 möjliga utfall • Ett annat efterföljande experiment har m 2 möjliga utfall • Vi gör först det ena sedan det andra experimentet • Totalt finns det m 1 × m 2 möjliga utfall. n

Repe titio Kombinatorik, forts. • Dragning utan återläggning – Vi drar en kula slumpmässigt och noterar dess nummer och lägger inte tillbaks den inför nästa dragning – Vi kan bara få ett nummer en gång • Dragning med återläggning – Vi drar en kula slumpmässigt och noterar dess nummer och lägger tillbaks den inför nästa dragning – Vi kan dra samma nummer flera gånger i en sekvens av dragningar n

Repe titio Kombinatorik, forts. n • Ordnad – Vi drar ett antal kulor slumpmässigt och noterar deras nummer – Ordningen spelar roll, dvs. vi skiljer t. ex. på (1, 2, 5), (1, 5, 2), (2, 1, 5), (2, 5, 1), (5, 1, 2) och (5, 2, 1) • Ej ordnad – Vi drar ett antal kulor slumpmässigt och noterar deras nummer – Ordningen spelar ingen roll, utfallen ovan betraktas som samma utfall Om vi har dragit k olika nummer av n möjliga, hur många sätt kan de ordnas på?

Repe titio Kombinatorik, forts. n Permutationer • Ett arrangemang av k olika objekt i en bestämd ordning kallas för en permutation av objekten. • Hur många olika permutationer kan man bilda av k olika objekt? • Antalet olika permutationer av k olika objekt är: k! = k × (k-1) × … × 3 × 2 × 1 • k-fakultet; (eng. k factorial)

Repe titio Kombinatorik, forts. Ordnat med återläggning • Dra k stycken ur n möjliga. • 1: a kulan n möjligheter, 2: a kulan n möjligheter, osv. … • Multiplikationsprincipen ger n

Repe titio Kombinatorik, forts. Ordnat utan återläggning • Dra k stycken ur n möjliga. • 1: a kulan n möjligheter, 2: a kulan (n-1) möjligheter, osv. … • Multiplikationsprincipen ger k stycken faktorer n

Kombinatorik, forts. • Antag att vi har n = 5 objekt A, B, C, D, E och att vi slumpmässigt väljer k = 3. • Vi kan få n!/(n-k)! = 5! / (5 -3)! = 60 olika utfall om vi tar hänsyn till ordningen. • Av alla dessa 60 utfall, hur många innehåller objekten A, B och C? • Svar: Vi kan lista dem: ABC, ACB, BAC, BCA, CAB, CBA; 6 utfall Eller inse att de k objekten kan ordnas på k! = 3! = 6 sätt

Kombinatorik, forts. Ej ordnat utan återläggning • Dra k stycken ur n möjliga. • 1: a kulan n möjligheter, 2: a kulan (n-1) möjligheter, osv. … Ger • Justera sedan för att ordningen inte spelar roll genom att dela med antal möjliga permutationer av k objekt →

Kombinatorik, forts. Kombinationer • Välja ut k objekt från n objekt där k ≤ n, och strunta i ordningen • ”n över k”, binomialkoefficient • Pascals triangel • k: te koeffeicienten i (a+b)n

Kombinatorik, forts. Kombinationer • Några särskilda resultat: Ex. På hur många sätt kan man dra fem kort ur en vanlig kortlek?

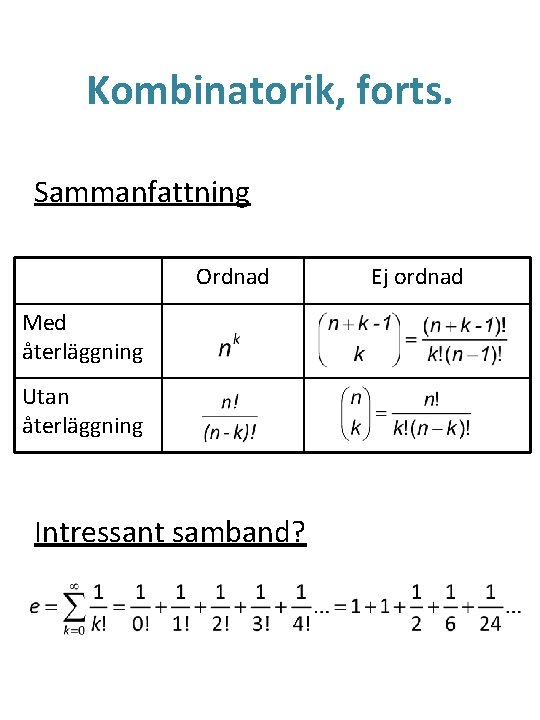
Kombinatorik, forts. Sammanfattning Ordnad Med återläggning Utan återläggning Intressant samband? Ej ordnad

Exempel • Hur många olika urval kan vi dra från Sveriges befolkning (n = ca 9 miljoner) av storlek k = 1000? Ej ordnad Utan återl. Med återl. … 4382 siffror till Ordnad Utan återl. Med återl. … 6950 siffror till

Sannolikheter Att beräkna sannolikheter • Händelser; A, B, C osv. • Sannolikheten för att A ska inträffa; P(A) • • • Alla händelser; Omöjlig händelse; Säker händelse; A och/eller B (union); A och B (snitt); Inte A (komplement); 0 ≤ P(A) ≤ 1 P(∅) = 0 P(Ω) = 1 P(A ∪ B) P(A ∩ B) P(Ā) = 1 - P(A)

Additionssatsen Sannolikheten att A eller B eller både A och B inträffar. • P(A ∪ B) = P(A) + P(B) – P(A ∩ B) • Specialfall om A och B disjunkta dvs. A ∩ B = ∅ vilket ger P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = P(A) + P(B) – P(∅) = P(A) + P(B) Jmfr med Kolmogorovs axiom

Exempel Dra ett kort ur en kortlek och låt A = Hjärter, B = Klätt, C = Spader Kung • P(A) = 13/52 = 1/4 P(B) = 12/52 = 3/13 P(C) = 1/52 • P(A ∩ B) = P(”Klätt hjärter”) = 3/52 • P(A ∪ B) = P(”Hjärter och/eller Klätt”) = P(A) + P(B) – P(A ∩ B) = 1/4 + 3/13 – 3/52 = (13+12 -3)/52 = 22/52 = 11/26 • P(A ∪ C) = P(”hj och/eller sp. K”) = P(A) + P(B) – P(A ∩ B) = (13+1)/52

Addera mera Tre händelser A, B och C • P(A ∪ B ∪ C) = P(A) + P(B) – P(A ∩ C) – P(B ∩ C) + P(A ∩ B ∩ C) • Rita ett Venndiagram! Övning: A = Hjärter, B = Klätt, C = jämnt (dam = 12, ess = 1). Beräkna varje term i additionssatsen ovan!

Betingade sannolikheter Sannolikheten att A inträffar givet att B inträffar eller har inträffat. Exempel: • Sannolikheten att det blev 6 givet att det blev jämnt? • Sannolikheten att det blev 6 givet att det blev udda? • Sannolikheten att det blev 6 givet att det inte blev 5? Vad är det som händer med utfallsrummet?

Betingning • Genom att händelsen B har inträffat så kan vi säga att utfallsrummet Ω har påverkats. • B har inte hänt, dvs. vi kan stryka bort den delen av Ω. • Sannolikheten för A beräknas genom att titta på den del av A som sammanfaller med B dvs. snittet och jämföra med B

Betingning Dvs. istället för att titta på stlk(A) / stlk(Ω) = P(A) (Klassiska tolkningen) tittar vi på stlk(A ∩ B) / stlk(B) = P(A|B) utläses ”sannolikheten för A givet B” och beräknas enligt

Betingning, forts. Vi kan även uttrycka det som P(A ∩ B) = P(A | B) ∙ P(B) Vi kan även vända på betingningen och se på sannolikheten att B har inträffat givet A: eller P(A ∩ B) = P(B|A) ∙ P(A) och därmed att P(A|B) ∙ P(B) = P(B|A) ∙ P(A)

Exempel Ibland är faktiskt de betingade sannolikheterna kända snarare än snittet. T. ex. Man har två modeller av en produkt i lager, 30 % av en gammal modell M 1 och 70 % av en nyare M 2. Av M 1 brukar 8 % vara behäftade med fel (händelse F) av den M 2 brukar 3 % vara fel. Om man tar en enhet på måfå ur lagret, vad är sannolikheten att a) det är fel på den? b) det är M 1 givet att det är fel på den?

Exempel, forts. a) P(F) Obs! M 1 = M 2 = P(F ∩ M 1) + P(F ∩ M 2) = P(F|M 1) ∙P(M 1) + P(F|M 2) ∙P(M 2) = 0, 08 ∙ 0, 3 + 0, 03 ∙ 0, 7 = 0, 045 dvs. 4, 5 % b) P(M 1|F) = P(F|M 1)∙P(M 1) / P(F) = 0, 08 ∙ 0, 7 / 0, 045 = 0, 53333 dvs. ca 53 % Är detta vettiga svar?

Oberoende: Exempel 2 Slumpmässigt urval av n = 2 ur en grupp av N = 10 objekt. Vi drar först en (experiment 1) och sedan en till (experiment 2) Är experimenten oberoende? • om det sker med återläggning • om det sker utan återläggning

Oberoende: Exempel 1 Vi fångar en fisk i en sjö. Vi noterar kön, mäter vikt och längd, bedömer eventuella skador etc. Vi kastar sedan tillbaks den. Vi upprepar detta k gånger. • Är fångsterna oberoende? • Hur kan våra mätresultat och observationer eventuellt påverkas om det finns ett beroende?

Oberoende: Exempel 3 Ex) Du är i Stockholm och en kompis i Las Vegas och ni kastar samtidigt varsin rättvis tärning. Vi vet (antar) att P(Xdu = 6) = P(Xkompis = 6) = 1/6 • Vad är sannolikheten att ni båda får en sexa? Dvs. P(Xdu = 6 ∩ P(Xkompis = 6) • Vad är sannolikheten att din kompis fick en sexa givet att du fick det? Dvs. P(Xkompis = 6 ∣ Xdu = 6 )

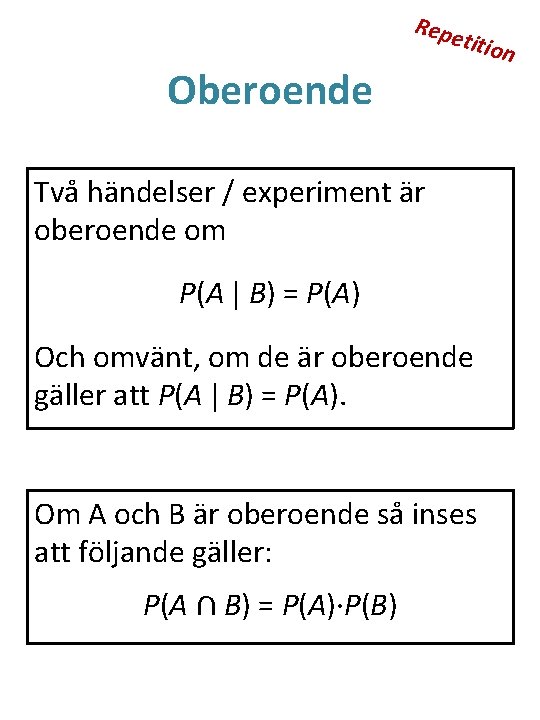
Oberoende Två händelser / experiment är oberoende om P(A | B) = P(A) Och omvänt om man kan visa att de är oberoende så är P(A | B) = P(A). Om A och B är oberoende så inses att följande gäller: P(A ∩ B) = P(A)∙P(B)

Oberoende Hur ser vi det sista? Jo, Om A och B är oberoende, så är de även oberoende av varandras komplement och komplementen är också oberoende av varandra. Dvs. varje par är också oberoende

F 6 Nyquist kap 6 – Vad är en stokastisk variabel – Diskreta och kontinuerliga sv – Frekvensfunktion (diskr. ) – Täthetsfunktion (kont. ) – Fördelningsfunktion • Men först lite repetition – Additionssatsen – Betingade sannolikheter – Oberoende

Repe Additionssatsen titio n Sannolikheten att A eller B eller både A och B inträffar. • P(A ∪ B) = P(A) + P(B) – P(A ∩ B) • Specialfall om A och B disjunkta dvs. A ∩ B = ∅ vilket ger P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = P(A) + P(B) – P(∅) = P(A) + P(B) Jmfr med Kolmogorovs axiom

Exempel Vi vet vad P(A ∩ B) är, beräkna Additionssatsen Sannolikheter för komplement Kräver lite tankearbete…

Repe titio Betingning Dvs. istället för att titta på stlk(A) / stlk(Ω) = P(A) (Klassiska tolkningen) tittar vi på stlk(A ∩ B) / stlk(B) = P(A|B) utläses ”sannolikheten för A givet B” och beräknas enligt n

Repe Betingning, forts. titio Vi kan även uttrycka det som P(A ∩ B) = P(A | B) ∙ P(B) Vi kan även vända på betingningen och se på sannolikheten att B har inträffat givet A: eller P(A ∩ B) = P(B|A) ∙ P(A) och därmed att P(A|B) ∙ P(B) = P(B|A) ∙ P(A) n

Repe Oberoende titio Två händelser / experiment är oberoende om P(A | B) = P(A) Och omvänt, om de är oberoende gäller att P(A | B) = P(A). Om A och B är oberoende så inses att följande gäller: P(A ∩ B) = P(A)∙P(B) n

Exempel Antag att vi har följande sannolikheter: P(A) = 0, 8; P(B) = 0, 2; P(A ∩ B) = 0, 16 a) Beräkna den betingade sannolikheten för A givet B b) Är A och B oberoende? a) Beräkna P(Ā ∩ B)

Övning Antag att vi har följande sannolikheter: A Ā a) b) c) d) e) f) g) E 1 0, 12 0, 07 E 2 0, 48 0, 06 Beräkna P(A ∩ E 1) Beräkna P(A|E 3) Är A och E 3 oberoende? Beräkna P(E 1|Ā) Är E 1 och Ā oberoende? Beräkna P(A) Beräkna P(E 3) E 3 0, 19 0, 08

Övning, forts. a) P(A ∩ E 1) = [avläst från tabellen] = 0, 12 b) P(A|E 3) = P(A ∩ E 3) / P(E 3) = P(A ∩ E 3) / [P(A ∩ E 3) + P(Ā ∩ E 3) ] = 0, 19 / (0, 19 + 0, 08) ≈ 0, 704 c) P(A) = [P(A ∩ E 1) + P(A ∩ E 2) + P(A ∩ E 3)] = 0, 12 + 0, 48 + 0, 19 = 0, 79 ≠ 0, 704 (från b) ⟹ A och E 3 är beroende. d) P(E 1|Ā) = P(Ā ∩ E 1) / P(Ā) = P(Ā ∩ E 1) / [P(Ā∩E 1)+P(Ā∩E 3)+P(Ā∩E 2)] = 0, 07 / (0, 07 + 0, 06 + 0, 08) ≈ 0, 333 e) P(E 1) = [analogt med c] = 0, 19 ≠ 0, 333 f) P(A) = [från c] = 0, 79 g) P(E 3) = [från b] = 0, 27

Stokastiska variabler 1 • Utfall av ett experiment och som resulterar i en siffra – ”hur mycket”, hur länge” osv. • Variabler: något som varierar, typiskt ett tal • Stokastiska variabler: något som varierar slumpmässigt • Kallas även slumpvariabel (s. v. ) • Betecknas typiskt med stor bokstav: X, Y, Z osv.

Stokastiska variabler 2 Ett utfall eller händelse beskrivs med den valda bokstaven, t. ex. X = 2, X = 10, X = -0, 25 X ≤ 3, X > 40, X ≠ 0, 4 eller allmänt X = x, X ≤ x, osv. ”X = x” och liknande betecknar alltså en händelse/utfall. Sedan vill vi veta P(X = x) för olika x

Stokastiska variabler 3 Sannolikhetsmodell • Ett utfallsrum Ω • Sannolikheter P(A) för alla händelser A ⊆ Ω På motsvarande sätt kan vi formulera en modell när vi har en stokastisk variabel • Utfallsrum Ω: x = …. . • Sannolikheter P(A): P(X = x), P(X ≤ x), osv. Alla tillåtna tal för x

Exempel Vi kastar en tärning tre gånger och noterar hur många ettor vi får. Beteckna med Ai att det blev en etta i kast nr i = 1, 2, 3. Är kasten oberoende? Möjliga utfall (Ω): Ā1, Ā 2, Ā 3 Ā1, Ā 2, A 3 Ā1, A 2, Ā 3 A 1, Ā 2, Ā 3 Ā1, A 2, A 3 A 1, Ā 2, A 3 A 1, A 2, Ā 3 A 1, A 2, A 3

Exempel, forts. Möjliga utfall som den stokastiska variabeln X kan anta: Ωx = {0, 1, 2, 3} el. x = 0, 1, 2, 3 Sannolikheterna för alla A ⊆ Ωx beräknas genom att summera alla utfall för de utfall som leder till A. a) b) c) d) Vad är sannolikheten för X = 0? För X > 2? = P(X=3) För X ≥ 2? För X = 4?

Exempel, forts. a) P(X = 0) = P(Ā1 ∩ Ā2 ∩ Ā3) = = [ty oberoende] = = P(Ā1)∙P(Ā2)∙P( Ā3) = (5/6)3 = = 125/216 ≈ 0, 579 b) P(X = 3) = P(A 1 ∩ A 2 ∩ A 3) = = [ty oberoende] = = P(A 1)∙P(A 2)∙P( A 3) = (1/6)3 = = 1/216 ≈ 0, 00463 c) P(X ≥ 2) = P(X=2) + P(X=3) = 16/216 d) P(X = 4) = 0, ty 4 ∉ Ωx

Diskreta mängder kan ses som en ”lista” av värden. Består av enstaka värden, oftast heltal. T. ex. {0, 1, 2, 3} {0, ± 1, ± 2, ± 3} {1, 1, 2, 3, 5} Även oändliga diskreta mängder kan förekomma. T. ex. {0, 1, 2, 3, …} {0, ± 1, ± 2, ± 3, …} {1, 1, 2, 3, 5, 8, 13, 21, …}

Kontinuerliga mängder kan typiskt beskrivas med intervall. Består av samtliga värden inom ett väldefinierat område. [0, 1] Slutna intervall [. . . , …] inkluderar ändpunkterna (0, 5) ∪ (10, 15) Öppna intervall (…, …) exkluderar ändpunkterna (1, 2] Intervallgränserna kan vara oändliga (då anges gränsen som öppet). T. ex. [0, ∞) , (-∞, ∞)

Frekvensfunktionen 1 Om Ωx för en s. v. X är diskret, kallas X en diskret s. v. Frekvensfunktionen för en diskret s. v. definieras som sannolikheten att X blir x och betecknas ofta med f(x) = P(X = x) Exempel: Ωx = {0, 1} och

Frekvensfunktionen 2 Frekvensfunktionen tillsammans med en tydlig beskrivning av utfallsrummet sammanfattar allt vi behöver veta om X. Frekvensfunktionen kallas även sannolikhetsfunktionen ty den ger oss just sannolikheterna för samtliga x som ligger i Ωx Eng. frequency or probability mass function. Frekvensfunktionen illustreras ofta i stolpdiagram där höjden på varje stolpe är lika med sannolikheten för motsvarande värde på x.

Exempel Antag följande frekvensfunktion: x 0 1 2 f(x) 0, 5787 0, 3472 0, 06944 F(x) 0, 5787 0, 9259 0, 9953 3 0, 00463 1 • Rita f(x) i ett lämpligt diagram! • Vad är F(x) för något? Om vi summerar f(x) för alla värden på x ∈ Ωx, vad blir summan?

Täthetsfunktionen 1 Om Ωx för en s. v. X är kontinuerlig, kallas X en kontinuerlig s. v. Täthetsfunktionen för en kontinuerlig s. v. definieras inte som sannolikheten att X blir x. Betecknas också ofta med f(x). Täthetsfunktionen är en beskrivning av hur sannolikt det är att X hamnar i ett delintervall till Ωx (Se Figur 6. 2, sid 7 Kap 6 i Nyquist)

Täthetsfunktionen 2 För att beräkna en sannolikhet att X ska ligga i intervallet mellan säg a och b, beräknas arenan under f(x) och över xaxeln och mellan a och b. Detta kan skrivas som en integral: P(a ≤ X ≤ b) = Vi kan lämna ena sidan odefinierad också och skriver P(X ≤ c) = Notera gränsen. Vad betyder det?

Täthetsfunktionen 3 Vi definierar en täthetsfunktion för en kontinuerlig s. v. i stil med Det finns vissa krav på hur funktionen får se ut: • f(x) ska vara kontinuerlig (betyder? ) • f(x) > 0 för alla x ∈ Ωx och = 0 annars • Arean under f(x) mellan ±∞ ska vara =?

Fördelningsfunktionen För både diskreta och kontinuerliga s. v. definieras fördelningsfunktionen enligt F(x) = P(X ≤ x) Diskreta fallet: Kontinuerliga fallet: