Exponents and Logarithms Definition of a Logarithm Rules

Exponents and Logarithms ª Definition of a Logarithm ª Rules ª Functions ª Graphs ª Solving Equations ©Carolyn C. Wheater, 2000 1

Definition of a Logarithm ª A logarithm, or log, is defined in terms of an exponential. ª If bx=a, then logba=x © If 52=25 then log 525=2 © log 525=2 is read “the log base 5 of 25 is 2. ” © You might say the log is the exponent we put on 5 to make 25 ©Carolyn C. Wheater, 2000 2

Rules for Exponents ª Exponents give us many shortcuts for multiplying and dividing quickly. ª Each of the key rules for exponents has an important parallel in the world of logarithms. ©Carolyn C. Wheater, 2000 3

Multiplying with Exponents ª To multiply powers of the same base, keep the base and add the exponents. Can’t do anything about the y 3 because it’s not the same base. Keep x, add exponents 7 + 5 ©Carolyn C. Wheater, 2000 4

Dividing with Exponents ª To divide powers of the same base, keep the base and subtract the exponents. Keep 7, subtract 10 -6 Keep 5, subtract 12 -4 ©Carolyn C. Wheater, 2000 5

Powers with Exponents ª To raise a power to a power, keep the base and multiply the exponents. This means t 7·t 7 = t 7+7+7 ©Carolyn C. Wheater, 2000 6

Rules for Logarithms ª Just as the rules for exponents let you easily rewrite a product, quotient, or power, the corresponding rules for logs allow you to rewrite the log of a product, the log of a quotient, or the log of a power. ©Carolyn C. Wheater, 2000 7

Log of a Product ª Logs are exponents in disguise © To multiply powers, add exponents © To find the log of a product, add the logs of the factors ª The log of a product is the sum of the logs of the factors ©logbxy = logbx + logby ©log 5(25· 125) = log 525 + log 5125 ©Carolyn C. Wheater, 2000 8

Log of a Product ª Think about it: © 25· 125 = 52 · 53 = 52+3=55 Laws of Exponents © log 5(25 · 125) = log 5(52 · 53)=log 5(52)+log 5(53) ¨ log 525 = log 5(52)=2 ¨ log 5125 = log 5(53)=3 Logs are Exponents! Add the exponents! © log 5(25 · 125) = log 5(52)+log 5(53) = 2 + 3 = 5 © log 5(25 · 125) = log 5(55) =5 ©Carolyn C. Wheater, 2000 9

Log of a Quotient ª Logs are exponents © To divide powers, subtract exponents © To find the log of a quotient, subtract the logs ª The log of a quotient is the difference of the logs of the factors © logb = logbx - logby © log 5(125 25) = log 5125 - log 525 ©Carolyn C. Wheater, 2000 10

Log of a Quotient ª Think about it: © 125 25 = 53 52 = 53 -2=51 Laws of Exponents © log 5(125 25) = log 5(53 52) = log 5(53) - log 5(52) ¨ log 5125 = log 5(53)=3 ¨ log 525 = log 5(52)=2 Logs are Exponents! Subtract the exponents! © log 5(125 125) = log 5(53)-log 5(52) = 3 - 2 = 1 © log 5(125 25) = log 5(51) =1 ©Carolyn C. Wheater, 2000 11

Log of a Power ª Logs are exponents © To raise a power to a power, multiply exponents © To find the log of a power, multiply the exponent by the log of the base ª The log of a power is the product of the exponent and the log of the base © logbxn = nlogbx © log 32 = 2 log 3 ©Carolyn C. Wheater, 2000 12

Log of a Power ª Think about it: © 252 =( 52)2 = 52 · 2=54 Laws of Exponents © log 5(252) = 2 log 5(52) ¨ log 525 = log 5(52)=2 ©log 5(252) = 2 log 5(52) = 2 · 2 = 4 Logs are Exponents! Multiply the exponent by the log (an exponent!) © log 5(252) = log 5(625) = log 5(54) = 4 ©Carolyn C. Wheater, 2000 13

Rules for Logarithms ª The same rules can be used to turn an expression into a single log. © logbx + logby = logbxy © logbx - logby = logb © nlogbx = logbxn ©Carolyn C. Wheater, 2000 14

Rules for Logarithms ª A sum of two logs becomes the log of a product. © log 39 + log 327 = log 3(9· 27) ª A difference of two logs becomes the log of a quotient. © log 232 - log 28 = log 2 Bases must be the same ª A multiple of a log becomes the log of a power © 2 log 57 = log 572 ©Carolyn C. Wheater, 2000 15

Sample Problem ª Express as a single logarithm: 3 log 7 x + log 7(x+1) - 2 log 7(x+2) © 3 log 7 x = log 7 x 3 © 2 log 7(x+2) = log 7(x+2)2 log 7 x 3 + log 7(x+1) - log 7(x+2)2 © log 7 x 3 + log 7(x+1) = log 7(x 3·(x+1)) - log 7(x+2)2 © log 7(x 3·(x+1)) - log 7(x+2)2 = ©Carolyn C. Wheater, 2000 16

Exponential Functions ª The exponential function has the form f(x)=abx © a is the beginning, or initial amount © b is the base, the factor that represents the rate of increase © x is the exponent, often representing a period of time ©Carolyn C. Wheater, 2000 17

Logarithmic Functions ª The logarithmic function has the form f(x)=logbx © b is the base © x is the number © f(x) is the log (or disguised exponent) ©Carolyn C. Wheater, 2000 18

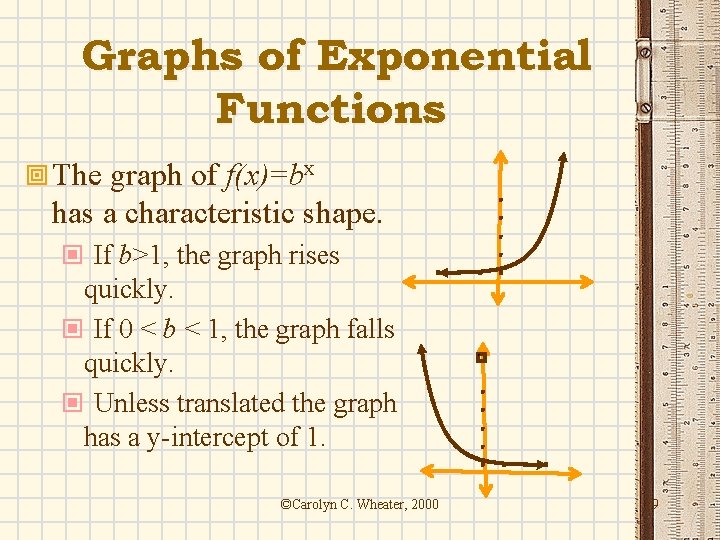
Graphs of Exponential Functions ª The graph of f(x)=bx has a characteristic shape. © If b>1, the graph rises quickly. © If 0 < b < 1, the graph falls quickly. © Unless translated the graph has a y-intercept of 1. ©Carolyn C. Wheater, 2000 24 19

Graphs of Logarithmic Functions ª The graph of f(x)=logbx has a characteristic shape. © The domain of the function is {x| x>0} -1 © Unless translated, the graph has an x-intercept of 1. 1 ©Carolyn C. Wheater, 2000 2 3 4 5 6 20

Translating the Graphs ª Both exponential and logarithmic functions can be translated. ª The vertical and horizontal slides will show up in predictable places in the equation, just as for parabolas and other functions. Shifted 1 unit right and 3 down ©Carolyn C. Wheater, 2000 Shifted 6 units left and 4 up 21

Solving Exponential Equations ª If possible, express both sides as powers of the same base ª Equate the exponents ª Solve ©Carolyn C. Wheater, 2000 22

Solving Exponential Equations ª If it is not possible to express both sides as powers of the same base © take the log of each side using any convenient base © use rules for logs to break down the expressions © isolate the variable © evaluate and check ©Carolyn C. Wheater, 2000 23

Solving Exponential Equations ª Solve © Take the log of each side © Use rules for logs ©Isolate the variable © Evaluate and check Any convenient base can be used, and since you’ll want to use your calculator, that will probably be 10 ©Carolyn C. Wheater, 2000 x 0. 675 24

Solving Logarithmic Equations ª Use the rules for logs to simplify each side of the equation until it is a single log or a constant. ©Carolyn C. Wheater, 2000 25

Solving Logarithmic Equations ª Log = Log ©Exponentiate (drop logs) © Solve the resulting equation © Reject solutions that would mean taking the log of a negative number ©Carolyn C. Wheater, 2000 26

Solving Logarithmic Equations ª Log = Constant ©Use the definition of a logarithm to express as an exponential ©Evaluate and check ©Carolyn C. Wheater, 2000 27