Example Control Flow Graphs Control Flow Graph Unity

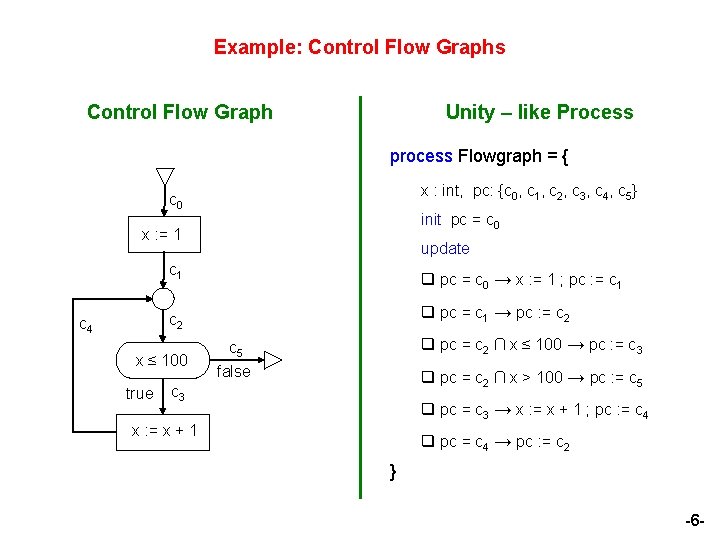
Example: Control Flow Graphs Control Flow Graph Unity – like Process process Flowgraph = { x : int, pc: {c 0, c 1, c 2, c 3, c 4, c 5} c 0 init pc = c 0 x : = 1 update c 1 q pc = c 0 → x : = 1 ; pc : = c 1 q pc = c 1 → pc : = c 2 c 4 x ≤ 100 true q pc = c 2 ∩ x ≤ 100 → pc : = c 3 c 5 false q pc = c 2 ∩ x > 100 → pc : = c 5 c 3 q pc = c 3 → x : = x + 1 ; pc : = c 4 x : = x + 1 q pc = c 4 → pc : = c 2 } -6 -

Example: Mutual Exclusion P = m : cobegin P 0 || P 1 coend m’ P = P 0 || P 1 P 0 : : l 0 : while true do { P 0 = { nc 0 : wait (turn = 0) cr 0 : turn : = 1 } turn : {0, 1} , pc 0 : { nc 0, cr 0} init pc 0 = nc 0 update q pc 0 = nc 0 ∩ turn = 0 → pc 0 : = cr 0 l 0’ : q pc 0 = nc 0 ∩ turn = 1 → pc 0 : = nc 0 P 1 : : l 1 : while true do { nc 1 : wait (turn = 1) cr 1 : turn : = 0 } l 1’ : q pc 0 = cr 0 → turn : = 1 ; pc 0 : = nc 0 } P 1 = { turn : {0, 1} , pc 1 : { nc 1, cr 1} init pc 1 = nc 1 update q pc 1 = nc 1 ∩ turn = 1 → pc 1 : = cr 1 Pseudo - code q pc 1 = nc 1 ∩ turn = 0 → pc 1 : = nc 1 q pc 1 = cr 1 → turn : = 0 ; pc 1 : = nc 1 } -7 -

Example: Mutual Exclusion Expanded process P = { turn : {0, 1} , pc 0 : { nc 0, cr 0} , pc 1 : { nc 1, cr 1} init pc 0 = nc 0 ∩ pc 1 = nc 1 update q pc 0 = nc 0 ∩ turn = 0 → pc 0 : = cr 0 q pc 0 = nc 0 ∩ turn = 1 → pc 0 : = nc 0 q pc 0 = cr 0 → turn : = 1 ; pc 0 : = nc 0 q pc 1 = nc 1 ∩ turn = 1 → pc 1 : = cr 1 q pc 1 = nc 1 ∩ turn = 0 → pc 1 : = nc 1 q pc 1 = cr 1 → turn : = 0 ; pc 1 : = nc 1 } -8 -

Example: Transition Relation Unity – like Process type arcs = {c 0, c 1, c 2, c 3, c 4, c 5} process Flowgraph = { x : int, pc: arcs init pc = c 0 update q pc = c 0 → x : = 1 ; pc : = c 1 Semantics Q = int x arcs ^ pc = c 0 = { (x, c 0) | x Є int } I= R ^= pc 0 = c 0 ∩ x’ = 1 ∩ pc’ : = c 1 U pc = c 1 ∩ pc’ : = c 2 U pc = c 2 ∩ x ≤ 100 ∩ pc’ : = c 3 U q pc = c 1 → pc : = c 2 pc = c 2 ∩ x > 100 ∩ pc’ : = c 5 U q pc = c 2 ∩ x ≤ 100 → pc : = c 3 pc = c 3 ∩ x’ = x + 1 ∩ pc’ : = c 4 U q pc = c 2 ∩ x > 100 → pc : = c 5 pc = c 4 ∩ pc’ : = c 2 q pc = c 3 → x : = x + 1 ; pc : = c 4 q pc = c 4 → pc : = c 2 } -9 -

Example: Predicate Transformers post [ pc = 2 ∩ x ≤ 100 → pc : = c 3 ](φ) = pc’, x’. pc’ = 2 ∩ x’ ≤ 100 ∩ pc = c 3 ∩ φ(pc’, x’) E ~ pre [ pc = 2 ∩ x ≤ 100 → pc : = c 3 ](φ) = pc’, x’. pc = 2 ∩ x ≤ 100 ∩ pc’ = 3 ═> φ(pc’, x’) = pc = 2 ∩ x ≤ 100 => φ[3/ pc’, x/ x’] -10 - A

Abstract Semantics of Programs Abstract State Graphs: S = (Q, v. Ti, I) state graph of the program QA a lattice of abstract states α : P(Q) → QA A Galois connection γ : QA → P(Q) α(γ(q)) = q φ ═> γ(α(φ)) given γ → α(φ) = ∏ {q Є QA | φ => γ(q)} SA = (QA, v. Ti. A, I A) is an abstraction of S iff (1) I γ (2) A Τi A γ(IA) i, q Є QA. Post [ Ti ](γ(q)) γ(Ti. A(q)) γ Τi Consequence: every concrete execution is represented by at least one abstract -11 -

Abstract State Lattice Main idea: Given {φ1, . . , φl } predicates on vars of concrete P. B 1, . . , Bl boolean variables (all concrete states that satisfy φi) Abstract states: set of predicates over B 1, . . , Bl (QA). Galois connection: γ(exp. A(B 1, . . , Bl )) = exp. A[φ�/ B�] α(φ)= Λ {exp. A(B 1, . . , Bl )| φ ═> exp. A[φ�/ B�] } -not easily computed ═> use apper approx (monomial) l α’(φ)= Λ {(Bi | φ ═> φi } i=1 Monomial on B 1, . . , Bl: conjunction of Bi’s and ¬Bi’s (at most once) Theorem: The set M of monomials on B 1. . Bl forms: - complete lattice and (α ; γ) Galois connection -12 -

Abstract Transitions Main idea: exp. A γ γ(exp. A) Ti A Ti Ti A (exp. A) = α(post[Ti ](γ(exp. A))) α( post[Ti ]( γ(exp. A))) Problem: difficult to compute. α post[Ti ](γ(exp. A)) Ti A (exp. A) = α’(post[Ti ](γ(exp. A))) Use monomial approximation α’ of α. Has following form: false Ti A (exp. A) = l Λ i=1 if exp. A[φ�/ B�] ═> ¬qi (3. 0) Bj if post[Ti ](exp. A[φ�/ B�]) ═> φj (3. 1) ¬Bj if post[Ti ](exp. A[φ�/ B�]) ═> ¬φj true otherwise (3. 2) otherwise (3. 3) By using (2. 1) and (2. 2) : (3. 1) Bj if exp. A[φ�/ B�] Λ qj ═> φj [ assi(x�)/ x�] -13 -

Abstract Successors Computing abstract successors: check validity of implications (3) - use a decision procedure (DP) - automatic theorem prover implementing such DPs. → for all i Є [1, . . , l ]. prove ( 3. 0 | 3. 1 | 3. 2 ) Imposibility of proving (3): - post[Ti ](exp. A[φ� / B�]) intersects both φj and ¬φj - abstract exp. A too big → cut in smaller pieces - because of monomials - abstract state space is too rough. - applied proof strategy is not powerful enough Abstract initial state: I A = α’(init) - in most practical cases, defines one value for most variables. - can be computed by evaluating φi -14 -