Estatstica Aplicao ao Sensoriamento Remoto SER 204 ANO

Estatística: Aplicação ao Sensoriamento Remoto SER 204 - ANO 2021 Técnicas de Reamostragem Camilo Daleles Rennó camilo. renno@inpe. br http: //www. dpi. inpe. br/~camilo/estatistica/

Distribuição Amostral Quando a amostra é pequena, certas suposições podem não ser válidas, dificultando a obtenção da distribuição amostral de um estimador qualquer. 2

Reamostragem A reamostragem é o nome que se dá a um conjunto de técnicas ou métodos que se baseiam em calcular estimativas a partir de repetidas amostragens dentro da mesma amostra (única). Estas técnicas se propõem a avaliar as incertezas relacionadas a obtenção de estatísticas com distribuições amostrais desconhecidas. Também podem ser utilizadas para avaliar a significância de testes cujas estatísticas básicas não têm suas propriedades bem estabelecidas ou cujas premissas não podem ser consideradas verdadeiras. Alguns testes não paramétricos fazem uso desta abordagem. Exemplos de técnicas de reamostragem: Testes de Aleatorização (Testes de Permutação) Jackknife Bootstrap Validação Cruzada 3

Testes de Aleatorização Testes de aleatorização (ou testes de permutação ou testes exatos) são típicos testes de significância onde a distribuição da estatística testada é obtida calculando-se todos os possíveis valores destatística rearranjando-se os valores da amostra considerando uma hipótese nula verdadeira. Nem sempre todos os rearranjos das amostras podem ser avaliados. Isso acontece quando as amostras são grandes. Nesse caso, faz-se uma simulação de modo a testar o maior número possível de rearranjos. Quanto maior o número de simulações melhor! 4

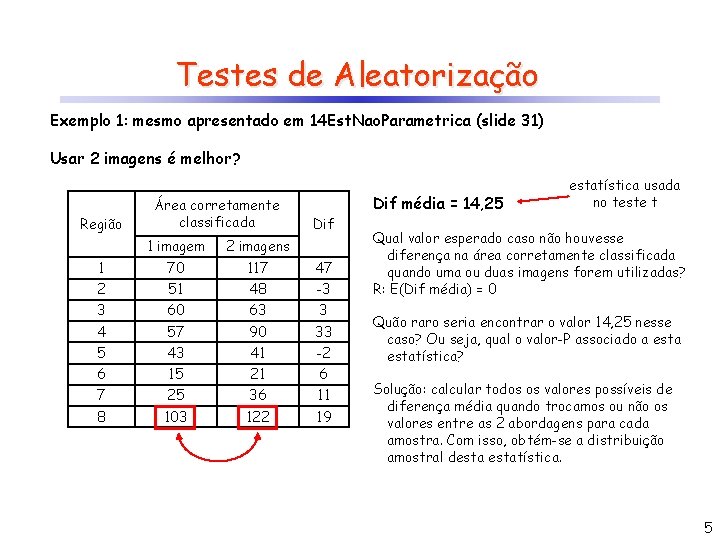
Testes de Aleatorização Exemplo 1: mesmo apresentado em 14 Est. Nao. Parametrica (slide 31) Usar 2 imagens é melhor? Região Área corretamente classificada Dif 1 imagem 2 imagens 1 70 117 47 2 51 48 -3 3 60 63 3 4 57 90 33 5 43 41 -2 6 15 21 6 7 25 36 11 8 103 122 19 Dif média = 14, 25 estatística usada no teste t Qual valor esperado caso não houvesse diferença na área corretamente classificada quando uma ou duas imagens forem utilizadas? R: E(Dif média) = 0 Quão raro seria encontrar o valor 14, 25 nesse caso? Ou seja, qual o valor-P associado a estatística? Solução: calcular todos os valores possíveis de diferença média quando trocamos ou não os valores entre as 2 abordagens para cada amostra. Com isso, obtém-se a distribuição amostral destatística. 5

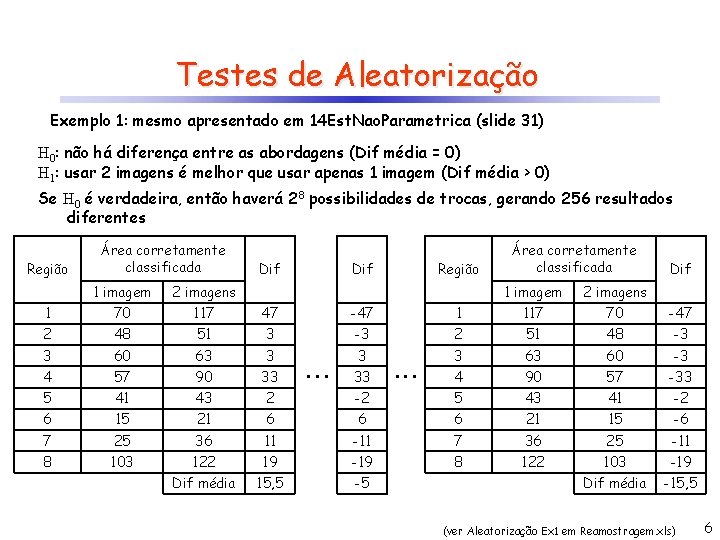
Testes de Aleatorização Exemplo 1: mesmo apresentado em 14 Est. Nao. Parametrica (slide 31) H 0: não há diferença entre as abordagens (Dif média = 0) H 1: usar 2 imagens é melhor que usar apenas 1 imagem (Dif média > 0) Se H 0 é verdadeira, então haverá 28 possibilidades de trocas, gerando 256 resultados diferentes Região Área corretamente classificada Dif 1 imagem 2 imagens 1 70 117 47 -47 2 48 51 3 3 60 63 3 4 57 90 33 5 41 43 2 6 15 21 7 25 8 103 Região Área corretamente classificada Dif 1 imagem 2 imagens 1 117 70 -47 -3 2 51 48 -3 3 3 63 60 -3 4 90 57 -33 -2 5 43 41 -2 6 6 6 21 15 -6 36 11 -11 7 36 25 -11 122 19 -19 8 122 103 -19 Dif média 15, 5 -5 Dif média -15, 5 . . . 33 . . . (ver Aleatorização Ex 1 em Reamostragem. xls) 6

Testes de Aleatorização Exemplo 1: mesmo apresentado em 14 Est. Nao. Parametrica (slide 31) H 0: não há diferença entre as abordagens (Dif média = 0) H 1: usar 2 imagens é melhor que usar apenas 1 imagem (Dif média > 0) Se H 0 é verdadeira, então haverá 28 possibilidades de trocas, gerando 256 resultados diferentes 97, 66% 14, 25 Valor-P = P(Dif média H 0 verdadeiro Dif média observada) = 2, 34% Conclusão: rejeita-se H 0 a 5% de significância, ou seja, é melhor usar 2 imagens 7

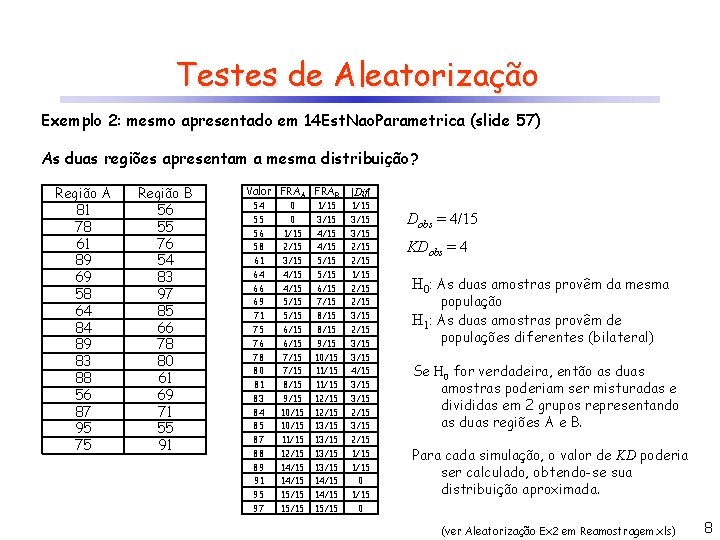
Testes de Aleatorização Exemplo 2: mesmo apresentado em 14 Est. Nao. Parametrica (slide 57) As duas regiões apresentam a mesma distribuição? Região A 81 78 61 89 69 58 64 84 89 83 88 56 87 95 75 Região B 56 55 76 54 83 97 85 66 78 80 61 69 71 55 91 Valor FRAA FRAB |Dif| 54 0 1/15 55 0 3/15 56 1/15 4/15 3/15 58 2/15 4/15 2/15 61 3/15 5/15 2/15 64 4/15 5/15 1/15 66 4/15 6/15 2/15 69 5/15 7/15 2/15 71 5/15 8/15 3/15 75 6/15 8/15 2/15 76 6/15 9/15 3/15 78 7/15 10/15 3/15 80 7/15 11/15 4/15 81 8/15 11/15 3/15 83 9/15 12/15 3/15 84 10/15 12/15 85 10/15 13/15 87 11/15 13/15 2/15 88 12/15 13/15 1/15 89 14/15 13/15 1/15 91 14/15 0 95 15/15 14/15 1/15 97 15/15 0 Dobs = 4/15 KDobs = 4 H 0: As duas amostras provêm da mesma população H 1: As duas amostras provêm de populações diferentes (bilateral) Se H 0 for verdadeira, então as duas amostras poderiam ser misturadas e divididas em 2 grupos representando as duas regiões A e B. Para cada simulação, o valor de KD poderia ser calculado, obtendo-se sua distribuição aproximada. (ver Aleatorização Ex 2 em Reamostragem. xls) 8

Testes de Aleatorização Exemplo 2: mesmo apresentado em 14 Est. Nao. Parametrica (slide 57) Simulando em R: reg. A<-c(81, 78, 61, 89, 69, 58, 64, 89, 83, 88, 56, 87, 95, 75) reg. B<-c(56, 55, 76, 54, 83, 97, 85, 66, 78, 80, 61, 69, 71, 55, 91) min<-min(reg. A, reg. B) max<-max(reg. A, reg. B) dif <- array(dim=max-min+1) for (i in min: max) dif[i-min+1]<-abs(length(which(reg. A <= i))-length(which(reg. B <= i))) KDobs<-max(dif) reg. AB<-c(reg. A, reg. B) n<-10000 KD<-array(dim=n) for (k in 1: n) { reg. AB<-sample(reg. AB) reg. At<-reg. AB[1: length(reg. A)] reg. Bt<-reg. AB[length(reg. A)+1: length(reg. AB)] for (i in min: max) dif[i-min+1]<-abs(length(which(reg. At <= i))-length(which(reg. Bt <= i))) KD[k]<-max(dif)} valor. P<-length(which(KD >= KDobs))/n valor. P d. KD<-cumsum(rev(table(KD))/n) KDcrit<-names(d. KD[max(which(d. KD<0. 05))]) KDcrit 9

Testes de Aleatorização Exemplo 2: mesmo apresentado em 14 Est. Nao. Parametrica (slide 57) As duas regiões apresentam a mesma distribuição? Região A 81 78 61 89 69 58 64 84 89 83 88 56 87 95 75 Região B 56 55 76 54 83 97 85 66 78 80 61 69 71 55 91 Dobs = 4/15 KDobs = 4 H 0: As duas amostras provêm da mesma população H 1: As duas amostras provêm de populações diferentes (bilateral) Valor-P = P(KD > KDobs) Pela simulação: Valor-P 62, 46% KDcrít 5% = 8 5% Conclusão: aceita-se H 0, ou seja, as duas amostras provêem da mesma população, adotando-se 5% de significância 10

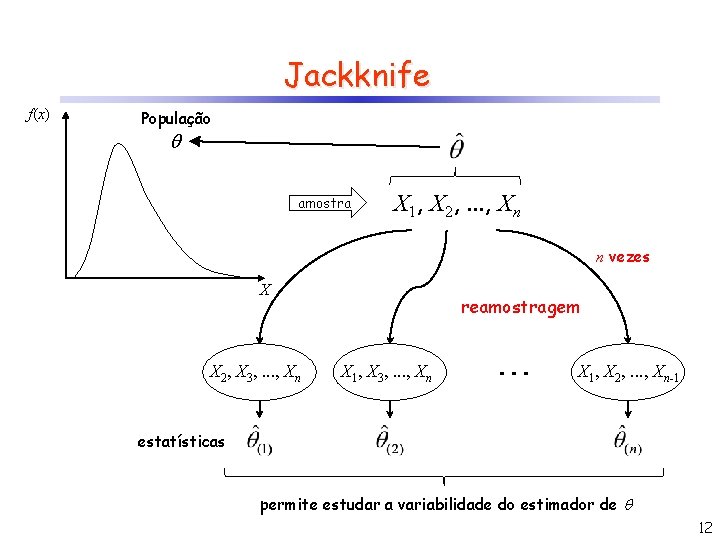
Jackknife Também chamado “leave-one-out test” Usado para estimar a variância e a tendência de um estimador qualquer. Baseia-se na remoção de 1 amostra (podendo ser mais) do conjunto total observado (n), recalculando-se o estimador a partir dos valores restantes (n-1). É de fácil implementação e possui número fixo de iterações (igual a n, caso se retire apenas 1 amostra por vez). 11

Jackknife f(x) População amostra X 1, X 2, . . . , Xn n vezes X X 2, X 3, . . . , Xn reamostragem X 1, X 3, . . . , Xn X 1, X 2, . . . , Xn-1 estatísticas permite estudar a variabilidade do estimador de 12

Jackknife Suponha que um determinado parâmetro possa ser estimado a partir de uma amostra de n valores, ou seja, Então a i-ésima replicação Jackknife corresponde ao valor estimado sem a amostra i: Com base nessas n estimativas, pode-se calcular então: onde (n grande) Efron, B. ; Stein, C. The Jacknife estimate of variance. The Annals of Statistics, 9(3): 586 -596. 1981 13

Jackknife Suponha que se deseja saber qual é a média geométrica de uma população e para isso obteve-se uma amostra de 10 valores: X 1 2 3 4 5 6 7 8 9 10 2, 2 3, 5 3, 4 6, 7 6, 2 8, 2 9, 2 7, 9 9, 0 10, 1 mg(i) 6, 688 6, 352 6, 372 5, 910 5, 961 5, 779 5, 705 5, 803 5, 719 5, 646 (ver exemplo JK em Reamostragem. xls) Qual é o valor da média geométrica desta amostra e qual a variância deste estimador? (amostra completa) 14

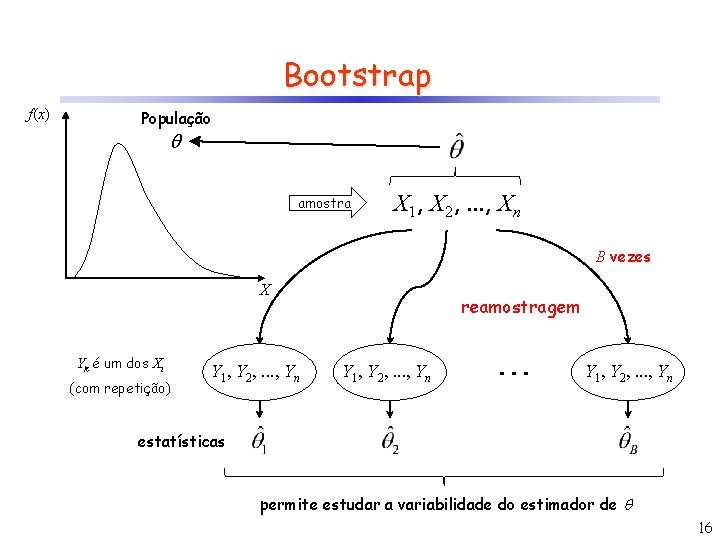
Bootstrap Pode ser considerado uma estratégia mais abrangente que o Jackknife por permitir um maior número de replicações. Também é usado para estimar a variância e a tendência de um estimador qualquer. Baseia-se na geração de uma nova amostra de mesmo tamanho da amostra original, a partir do sorteio aleatório com reposição de seus elementos. 15

Bootstrap f(x) População amostra X 1, X 2, . . . , Xn B vezes X Yk é um dos Xi (com repetição) Y 1, Y 2, . . . , Yn reamostragem Y 1, Y 2, . . . , Yn estatísticas permite estudar a variabilidade do estimador de 16

Bootstrap Suponha que um determinado parâmetro pode ser estimado a partir de uma amostra de n valores, ou seja, Então a cada iteração j, o valor estimado a partir da amostra será: onde yk é um dos valores da amostra (com reposição) Com base nas estimativas de B iterações, pode-se calcular então: (n grande) Recomenda-se que B 200, mas pode ser necessário B 2000 caso o objetivo seja construir intervalos de confiança para o parâmetro Efron, B. ; Hastie, T. 2016. Computer age statistical inference. Cambridge University Press. 17

Bootstrap Suponha que se deseja saber qual é a média geométrica de uma população e para isso obteve-se uma amostra de 10 valores: X 1 2 3 4 5 6 7 8 9 10 2, 2 3, 5 3, 4 6, 7 6, 2 8, 2 9, 2 7, 9 9, 0 10, 1 (ver exemplo BS em Reamostragem. xls) Qual é o valor da média geométrica desta amostra e qual a variância deste estimador? (amostra completa) 18

Validação Cruzada Tipicamente, na validação cruzada, a amostra é particionada aleatoriamente em dois subconjuntos: um de treinamento e outro de teste (validação). Esta técnica é aplicada principalmente quando um modelo é gerado e posteriormente este modelo é utilizado para se fazer predição. É importante observar que as avaliações feitas sobre o mesmo conjunto amostral de treinamento (única amostra) sempre são superestimadas, uma vez que o modelo encontrado tenta minimizar os erros de cada observação em relação ao modelo desejado. Para reduzir a casualidade do resultado encontrado após uma única divisão arbitrária, pode-se repetir o processo de partição aleatoriamente muitas vezes (podendo até testar todas possíveis!) e avaliar cada uma delas, sintetizando os resultados em uma medida de tendência central (média, mediana, etc), definindo um intervalo de credibilidade ou através de um boxplot. Outra abordagem bastante utilizada é reservar apenas 1 amostra por vez para teste e usar as demais para treinamento. Este método é conhecido como Validação Cruzada LOO (Leave One Out). 19

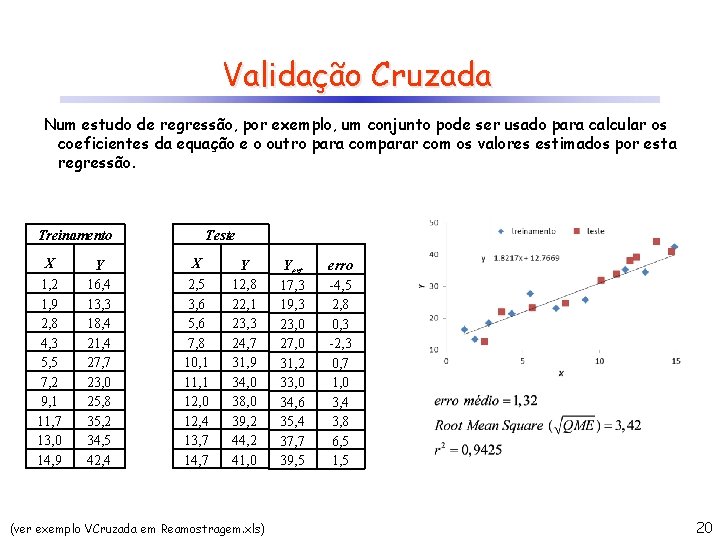
Validação Cruzada Num estudo de regressão, por exemplo, um conjunto pode ser usado para calcular os coeficientes da equação e o outro para comparar com os valores estimados por esta regressão. Treinamento X 1, 2 1, 9 2, 8 4, 3 5, 5 7, 2 9, 1 11, 7 13, 0 14, 9 Y 16, 4 13, 3 18, 4 21, 4 27, 7 23, 0 25, 8 35, 2 34, 5 42, 4 Teste X 2, 5 3, 6 5, 6 7, 8 10, 1 11, 1 12, 0 12, 4 13, 7 14, 7 Y 12, 8 22, 1 23, 3 24, 7 31, 9 34, 0 38, 0 39, 2 44, 2 41, 0 (ver exemplo VCruzada em Reamostragem. xls) Yest 17, 3 19, 3 23, 0 27, 0 31, 2 33, 0 34, 6 35, 4 37, 7 39, 5 erro -4, 5 2, 8 0, 3 -2, 3 0, 7 1, 0 3, 4 3, 8 6, 5 1, 5 20

Validação Cruzada Simulando inúmeras partições em R: x<-c(1. 2, 1. 9, 2. 8, 4. 3, 5. 5, 7. 2, 9. 1, 11. 7, 13, 14. 9, 2. 5, 3. 6, 5. 6, 7. 8, 10. 1, 11. 1, 12. 4, 13. 7, 14. 7), y<-c(16. 4, 13. 3, 18. 4, 21. 4, 27. 7, 23, 25. 8, 35. 2, 34. 5, 42. 4, 12. 8, 22. 1, 23. 3, 24. 7, 31. 9, 34, 38, 39. 2, 44. 2, 41) n<-length(x) xy<-rbind(x, y) r<-10000 em<-array(dim=r) rms<-array(dim=r) r 2<-array(dim=r) for (k in 1: r) { xy<-xy[, sample(n)] xytr<-xy[, 1: (n/2)] xytest<-xy[, ((n/2)+1): n] b<-(lm(xytr[2, ]~xytr[1, ]))$coefficients yest<-xytest[1, ]*b[2]+b[1] err<-xytest[2, ]-yest em[k]<-sum(err)/length(err) em<-sort(em) rms[k]<-sum(err^2)/(length(err)-1) em[r*c(. 025, . 975)] r 2[k]<-cor(yest, xytest[2, ])^2} rms<-sort(rms) boxplot(em) rms[r*c(. 025, . 975)] boxplot(rms) r 2<-sort(r 2) boxplot(r 2) r 2[r*c(. 025, . 975)] 21

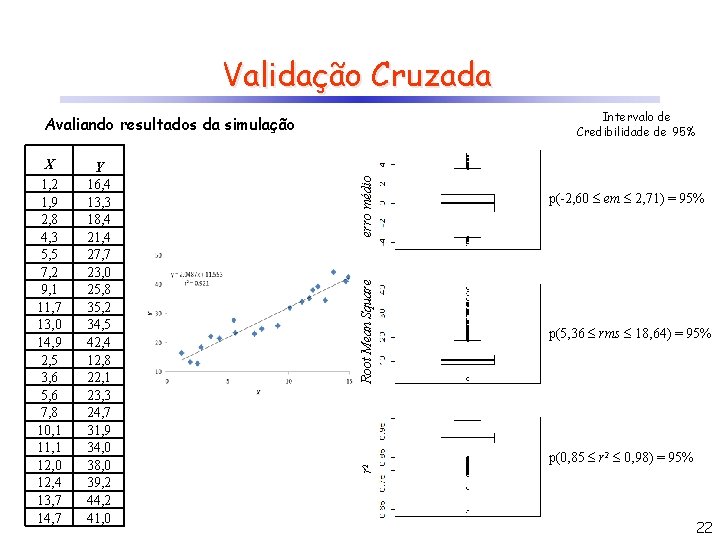
Validação Cruzada Intervalo de Credibilidade de 95% Root Mean Square Y 16, 4 13, 3 18, 4 21, 4 27, 7 23, 0 25, 8 35, 2 34, 5 42, 4 12, 8 22, 1 23, 3 24, 7 31, 9 34, 0 38, 0 39, 2 44, 2 41, 0 r 2 X 1, 2 1, 9 2, 8 4, 3 5, 5 7, 2 9, 1 11, 7 13, 0 14, 9 2, 5 3, 6 5, 6 7, 8 10, 1 11, 1 12, 0 12, 4 13, 7 14, 7 erro médio Avaliando resultados da simulação p(-2, 60 em 2, 71) = 95% p(5, 36 rms 18, 64) = 95% p(0, 85 r 2 0, 98) = 95% 22