Escuela N 1 Sagrada Familia Relaciones Proporcionales 8

Escuela Nº 1 “Sagrada Familia” Relaciones Proporcionales 8º año - NB 6 Profesor: Rigoberto Garrido M

RAZON: Se denomina razón, al cuociente entre dos magnitudes, distintas de cero, expresadas en la misma unidad. Ejemplo: Las edades de dos hermanos son 9 y 12 años, entonces la razón entre la edad del menor y del mayor es: o bien , 3 : 4 y se lee: " 3 es a 4 ".

PROPORCION: Una proporción está formada por dos razones iguales: a : b = c : d Donde a , b , c y d son distintos de cero y se lee " a es a b como c es a d ". Por ejemplo, 3 : 4 y 6 : 8 son dos razones iguales, entonces podemos construir la proporción: 3 : 4 = 6 : 8 Que se lee " 3 es a 4 como 6 es a 8 ".

TEOREMA FUNDAMENTAL: En cada proporción se cumple lo siguiente: a : b = c : d Û a d = b c Ejemplo: 3 : 4 = 6 : 8 Û 3 × 8 = 4 × 6

Aplicaciones: 1. Las alturas de dos edificios están en la razón 4 : 5. Si el primero mide 20 ( m ) , ¿cuánto mide el segundo? Respuesta: 20 x 5 = 4 x X 100 = 4 X 100 = X 4 25 = X Respuesta: El segundo edificio mide 25 ( m )

2. Dos amigos se reparten 42 bolitas en la razón 3 : 4. ¿Cuántas bolitas recibió cada uno? Respuesta: El primer amigo recibió 3 K bolitas El segundo amigo recibió 4 k bolitas 3 k + 4 k = 42 7 K = 42 K = 42 7 K = 6 El primer amigo recibió 3 × 6 = 18 bolitas El segundo amigo recibió 4 × 6 = 24 bolitas

PROPORCIONALIDAD DIRECTA: Dos variables son directamente proporcionales, si cambian en la misma razón, por ejemplo, si el valor de una se duplica, entonces el valor de la otra también se duplica. Algebraicamente esto se enuncia así: Sean x e y variables , entonces: También se puede expresar así: Ejemplo: Si 5 caramelos cuestan $ 200 , entonces 10 de esos mismos caramelos cuestan $ 400.

Aplicaciones: 1. 2. Si con $ 300 se pueden comprar 5 bombones, entonces ¿cuántos de esos mismos bombones se pueden adquirir con $ 420? Respuesta: 300 X = 420 x 5 X = 2100 300 X = 7 Respuesta: Se pueden comprar 7 bombones

2. Un poste de 4 ( m ) de altura, en cierto instante, da una sombra de 6 ( m ). ¿Cuánto mide de alto otro poste, si en ese mismo instante, da una sombra de 15 ( m )? Respuesta: 4 X 15 = 6 x 60 = 6 x 60 = X 6 10 = X El poste mide 10 ( m ) de altura

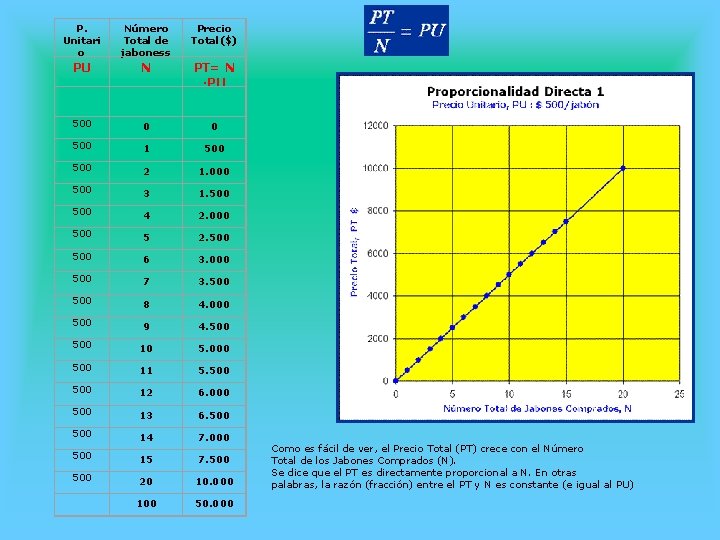
Proporcionalidad Directa I Supongamos que una familia necesita comprar jabones en un supermercado y que cada jabón cuesta $ 500. Se dice que el Precio Unitario (PU) es de $ 500 por jabón y se escribe El Precio Total (PT) de la compra de jabones depende, como es claro, del Precio Unitario de los jabones y del Número Total (N) de jabones comprados, de la siguiente manera En la Tabla 1 se resume esta situación para distintos Números Totales de jabones comprados

P. Unitari o Número Total de jaboness Precio Total($) PU N PT= N ·PU 0 0 1 500 2 1. 000 3 1. 500 4 2. 000 5 2. 500 6 3. 000 7 3. 500 8 4. 000 9 4. 500 500 500 10 5. 000 500 11 5. 500 12 6. 000 500 13 6. 500 14 7. 000 500 15 7. 500 20 10. 000 100 50. 000 Como es fácil de ver, el Precio Total (PT) crece con el Número Total de los Jabones Comprados (N). Se dice que el PT es directamente proporcional a N. En otras palabras, la razón (fracción) entre el PT y N es constante (e igual al PU)

PROPORCIONALIDAD INVERSA: Dos variables son inversamente proporcionales, si cambian en la razón inversa, por ejemplo, si el valor de una se duplica, entonces el valor de la otra se reduce a la mitad. Algebraicamente esto se enuncia así: Sean x e y variables , entonces: x y = constante Û x e y son inversamente proporcionales También se puede expresar así: x 1 y 1 = x 2 y 2 Û x e y son inversamente proporcionales

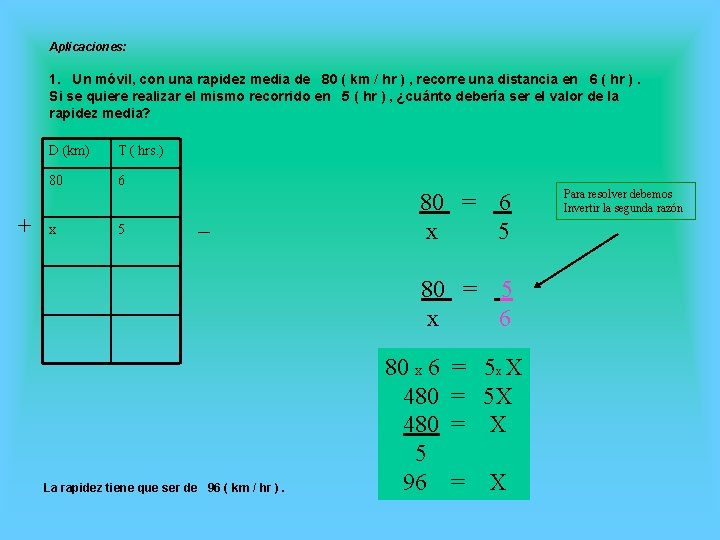
Aplicaciones: 1. Un móvil, con una rapidez media de 80 ( km / hr ) , recorre una distancia en 6 ( hr ). Si se quiere realizar el mismo recorrido en 5 ( hr ) , ¿cuánto debería ser el valor de la rapidez media? + D (km) T ( hrs. ) 80 6 x 5 _ 80 = 6 x 5 80 = 5 x 6 La rapidez tiene que ser de 96 ( km / hr ). 80 x 6 = 5 x X 480 = 5 X 480 = X 5 96 = X Para resolver debemos Invertir la segunda razón

2. Entre 4 personas pintan una casa en 3 días. ¿Cuántas personas se necesitan para realizar el mismo trabajo en dos día? Respuesta Nº personas + Nº días 4 3 x 2 _ 4 = 3 X 2 4 = 2 X 3 Se necesitan 6 personas 4 x 3 = 2 x X 12 = 2 X 12 = X 2 6 = X Para resolver debemos Invertir la segunda razón