Relaciones proporcionales w Razones w Proporcionalidad directa w

Relaciones proporcionales w Razones w. Proporcionalidad directa w. Proporcionalidad inversa

Razones w Es una comparación por cuociente entre dos magnitudes, donde la primera recibe el nombre de antecedente y la segunda, el nombre de consecuente Ejemplo: En un curso hay 12 mujeres y 16 hombres Razón: 12 o bien 12 : 16 16 En ambos casos se lee 12 es a 16 12 Antecedente 16 Consecuente

Proporciones Una proporción es una igualdad entre dos razones. Para comprobar si una proporción es verdadera se aplica producto cruzado Se escribe de la forma Ejemplo: A=C o bien a : b = c : d 3 = 12 3 x 16 = 4 x 12 B D 48 = 48 En ambos casos se lee: 4 16 “a es a b como c es a La proporción sí es verdadera d”

Proporcionalidad Directa Dos magnitudes son directamente proporcionales: w Al aumentar una de ellas, la otra también aumenta en la misma proporción w Al disminuir una de ellas, la otra también disminuye en la misma proporción Si dos magnitudes son directamente proporcionales: w El valor de la razón o cuociente entre las variables (k) se mantiene constante w Su gráfico son puntos pertenecientes a una misma recta que pasa por el origen

Ejemplo En una receta se incluyen tres huevos por cada 12 personas. ¿Cuántos huevos se necesitarán si se desea preparar la receta para 20 personas? Proporción: 12 = 3 20 X X = 20 x 3 X = 5 12 Por lo tanto, una receta para 20 personas necesita 5 huevos personas

Proporcionalidad Inversa Dos magnitudes son inversamente proporcionales si: w Al aumentar una de ellas en una cierta cantidad de veces, la otra disminuye en la misma proporción w Al disminuir una de ellas una cierta cantidad de veces, la otra aumenta en la misma proporción. Si dos magnitudes son inversamente proporcionales: w El producto entre las variables es constante, x · y = k w Su gráfico está constituido por puntos de una curva llamada hipérbola. Ésta no intersecta los ejes coordenados, solo se acerca a ellos

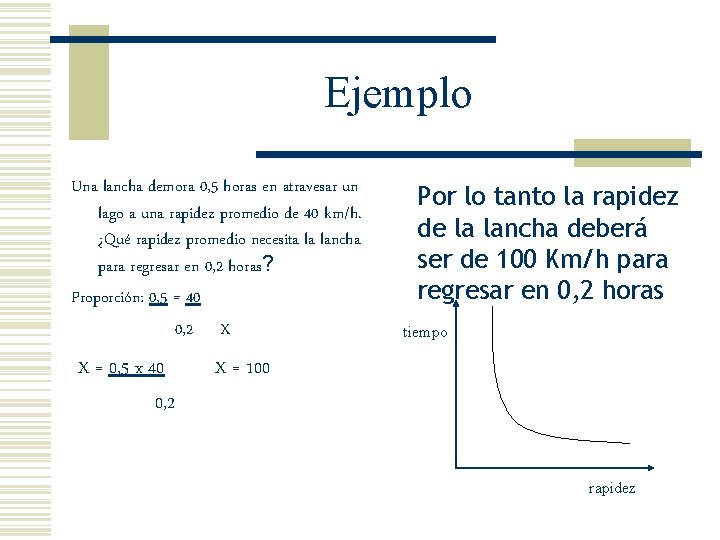
Ejemplo Una lancha demora 0, 5 horas en atravesar un lago a una rapidez promedio de 40 km/h. ¿Qué rapidez promedio necesita la lancha para regresar en 0, 2 horas? Proporción: 0, 5 = 40 0, 2 X X = 0, 5 x 40 0, 2 Por lo tanto la rapidez de la lancha deberá ser de 100 Km/h para regresar en 0, 2 horas tiempo X = 100 rapidez