Equivalence of Pushdown Automata and ContextFree Grammar Prof

Equivalence of Pushdown Automata and Context-Free Grammar Prof. Héctor Muñoz-Avila

Two Crucial Concepts • Nondeterministic computation – Give us flexibility for constructing devices and understanding the power/limitations of these devices • Induction – Allow us to prove statements that otherwise would be hard to see why they are true • In this class(es), we will illustrate these two powerful concepts once more

Class Convention regarding Transitions in Pushdown Automata • Strictly speaking, Transitions have the form: – : (Q × ( {e}) ) ( Q × ( {e}) ) • (q’, )) ((q, , )) q , q’ • We are going to allow to pop and push words in ( {e})* – Can we represent a transition that pops/pushes words in ( {e})* with transitions that pop/pushes characters in ( {e}) ? – Careful: order of pushing/popping individual characters matter! – To avoid confusion, view the stack as a word and push/pop as adding/removing strings prefix from that word

My Solution of the Homework • Construct a pushdown automaton for words in {a, b} such that the number of a’s is twice the number of b’s – 3 states – Pushing marker for bottom of stack – ….

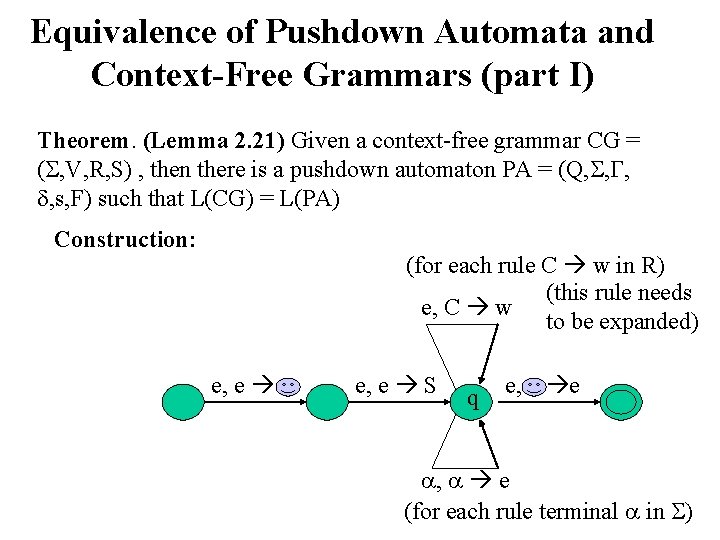
Equivalence of Pushdown Automata and Context-Free Grammars (part I) Theorem. (Lemma 2. 21) Given a context-free grammar CG = ( , V, R, S) , then there is a pushdown automaton PA = (Q, , , , s, F) such that L(CG) = L(PA) Construction: (for each rule C w in R) (this rule needs e, C w to be expanded) e, e S q e, e , e (for each rule terminal in )

Sketch of the Proof S 1 T 1 1 where 1, 1 are in * and T 1 is in ( V)* (taking the leftmost non terminal in T 1) 1 2 T 2 2 1 where 2 is in in * and T 2 is in ( V)* … (always taking the leftmost non terminal) 1 2… n n … 1 (q, 1 2… n n 1, S) * (q, 2… n n 1, 2 T 2 2 1) (q, 3… n n 2 1, T 2 2 1) * * (q, e, e) (q, 1 2… n n 1, 1 T 1 1) (q, 2… n n 1, T 1 1) (s, 1 2… n n 1, e) (Excluded for simplicity)

Equivalence of Pushdown Automata and Context-Free Grammars (Part II) Theorem. (Lemma 2. 27) Given a pushdown automata PA = (Q, , , , s, F) then, there exists a context-free grammar CG = ( , V, R, S) such that L(PA) = L(CG) Assumptions: 1. PA has only one accepting state 2. Stack is empty when accepting a word 3. Each transitions pops XOR pushes one element in the stack

Constructing the Grammar CG (1) • CG will contain the variables: Apq for every two states p and q in PA • Apq generates a word w PA empty-process w from p to q • PA empty-process w from p to q – w is given as input starting on state p with empty stack – then PA will nondeterministically process all characters in w • ending with the empty word in state q and the empty stack

Constructing the Grammar CG (2) • We are going to construct three kinds of rules for CG: – Apq a. Arsb for all p, q, r, s in Q, all a, b in ( {e}), and all t in such that the following two transitions occur in the PA: p s a, e t b, t e r q – Apq Apr Arq for all p, q, r in Q – App e for all p in Q That’s it! Can you see it?

Proving that CG is equivalent to PA (1) If Apq generates a word w then PA empty-process w from p to q • Proof by induction on # steps in Apq * w • Basis: # steps is 1 • Induction: holds for k # steps, need to prove for k+1 # steps – Two sub-cases depending of which rule was applied first: • Apq a. Arsb or • Apq Apr Arq

Proving that CG is equivalent to PA (2) If PA empty-process w from p to q then Apq generates a word w • Proof by induction on # steps in processing w • Basis: # steps is 0 • Induction: holds for k # steps, need to prove for k+1 # steps – Two sub-cases depending on the following: • Stack is empty only at the beginning and at the end of process or • Stack gets empty somewhere in-between

Corollary • • Let s be the start state in PA Let f be the accepting state in PA Therefore, Asf is the start variable in CG We just proved that: Asf generates a word w if and only if PA accepts w

Homework • Show that if L 1 and L 2 are context-free languages then: – L 1 L 2 is a context-free language – L 1 L 2 is a context-free language (hint: if L 1 and L 2 are context free, then there is two grammars G 1 generating L 1 and G 2 generating L 2. How can you combine G 1 and G 2 to generate the union and concatenation? ) • 2. 19 • 2. 23 • 2. 27