Engineering Optimization Chapter 7 Constrained direct search Part

Engineering Optimization Chapter 7: Constrained direct search (Part 2) Huy-Dung Han, Fabio E. Lapiccirella Department of Electrical and Computer Engineering University of California, Davis Advisors: Professor Xin Liu and Professor Zhi Ding Professor Biswanath Mukherjee’s group study

7. 3 RANDOM-SEARCH METHODS �Purpose �Locating feasible starting points �Locating the vicinity of the optimum � 2 methods �Direct Sampling Procedures �Strategies based on random-search procedures.

7. 3. 1 Direct Sampling Procedures. Simultaneous search �Randomize & find the optimum �To achieve the optimum with 90% confidence and the number of samples is in the order of �Eg:

Sampling with interval reduction �Series of Q simultaneous blocks. �P point per blocks �The best point of the pervious block initializes the current block. �The current block is executed with a reduced variable sampling range.

Sampling with interval reduction �Inputs �Initial feasible �Range estimate �reduction factor

Sampling with interval reduction �For each block q=1. . Q.

Example 7. 4 Fuel Allocation in Power Plants � 2 electric power generators �Combined power �Operating range �Generator 1 �Oil required �Gas required �Generator 2 �Oil required �Gas required �Fuel gas limitation: less than 10 unit/h

Example 7. 4 Fuel Allocation in Power Plants (cont. ) �Fuels can be combined in an additive fashion �to generate we need �Determine the output rate of each generator and the fuel mix fractions so as to minimize the total power consumption

Example 7. 4 Fuel Allocation in Power Plants (cont. ) �Minimize the oil consumption �Subject to �Availability of gas �Ouput power requirement

Example 7. 4 Result �Sampling with reduction interval method �Initial solution �Initial range estimate �Result �Cost � 0. 1% of the optimum: 55 blocks x 100 samples � 0. 01% of the optimum: 86 blocks x 100 samples

7. 3. 2 Combined Heuristic Procedures �Combine random sampling with heuristic rules �We investigate 2 methods �Adaptive Step-size random search �Combinatorial Heuristic Method

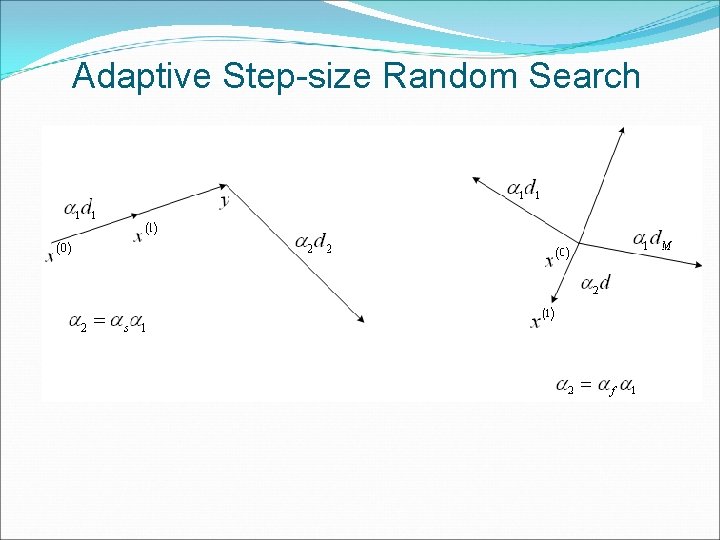
Adaptive Step-size Random Search �Search direction: random �Step length in that direction is determined by the previous history of successes and failures �If 2 successive steps lead to improvement, increase step size. �If M steps lead to no improvement, decrease step size �It finds a local optimum.

Adaptive Step-size Random Search �Input �Increase factor when success �Decrease factor when failure �Number of failure �Initial point �Initial �Step size �Failure counter

Adaptive Step-size Random Search �Step 1: �generate random direction vector �Calculate the next point �Step 2: � � �Step 3 � �

Adaptive Step-size Random Search �Step 4: �Step 5: � Check termination rule, if not, go to step 1

Adaptive Step-size Random Search

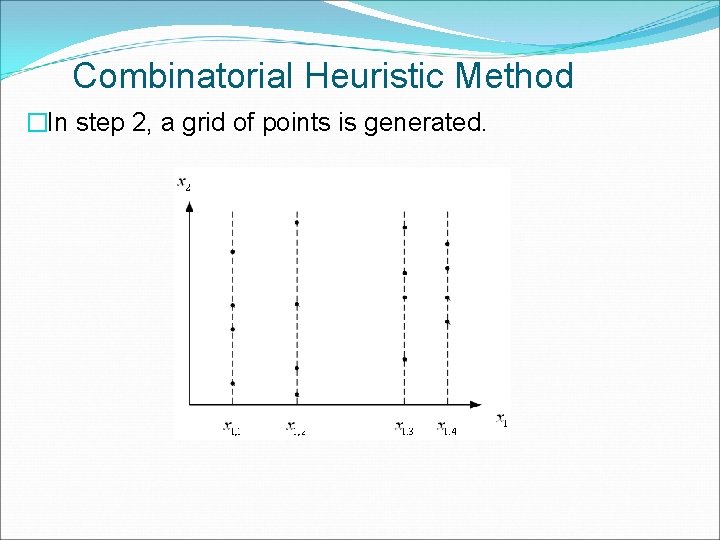
Combinatorial Heuristic Method �Approach �Discretizing the range of the independent variables �Randomized search over the resulting finite grid of possible solutions. �Step 1 (Initial step) �Given feasible starting point �For each variable , execute the loop of steps

Combinatorial Heuristic Method �Step 2: Optimize the i-th variable, (others are fixed) �(a) If found none, goto step 2 with variable i+1. �(b) �(c) Look ahead search � (i) if not goto step 2(a) with variable i+1 � (ii) find the best point and keep the value of i-th variable. �(d) If i=N, goto step 3. � Otherwise, goto step 2(a) with variable (i+1)

Combinatorial Heuristic Method �In step 2, a grid of points is generated.

Combinatorial Heuristic Method �Step 3: Special for i=N �Step 4: Check the termination. If not satisfied, go to step 2 with variable i=1

Discussion �Random-sampling-based search �Low-dimensionality problems �Generating good starting points for more sophisticated algorithm �If sampling strategy that covers most of the feasible region, it may locate the vicinity of the global optimum. �Identify the approximate neighborhood of the minimum �Quite effective for severely nonlinear problems that involve multiple local minima, low dimensionality.

Summary �Find constraint optima using only objective and constraints �Eliminate equality constraints. �Feasible starting point by randomization �Premature termination: if searches along a fixed set of directions. �Complex method �could fail if the feasible region is not convex. �Random-search: �Sequential sampling is preferable to simultaneous sampling. �Generate good feasible starting points. �Identify the vicinity of global solutions for problems with multiple local optima.