Constrained Optimization Pakistan Institute of Engineering and Applied

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Allah says ﺍ ﻱ ﺍﺍ ﺍ ﺍ ﺍ ﻭ ﻭﺍ ﻯ ﺍ ﻳ ﺍ ﻭﺍ ﻭ Nor are the two bodies of flowing water alike, - the one palatable, sweet, and pleasant to drink, and the other, salt and bitter. Yet from each (kind of water) do ye eat flesh fresh and tender, and ye extract ornaments to wear; and thou seest the ships therein that plough the waves, that ye may seek (thus) of the Bounty of Allah that ye may be grateful. Al-Qur'an, 035. 012 (Fatir [The Angels, Originator]) 1 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). A Tutorial on Constrained Optimization Lagrangian Functions and KKT Fayyaz ul Amir Afsar Minhas fayyazafsar@gmail. com Department of Computer and Information Sciences Pakistan Institute of Engineering and Applied Sciences (PIEAS) P. O. Nilore, Islamabad.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Contents § Introduction § Preliminaries § Convex Functions § Examples § Lagrangian Formulation of Constrained Optimization Problem § Optimality Conditions § Examples 3 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Introduction § The constrained optimization problem (COP) can be expressed in its general form as follows § Example 4 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Aims of the tutorial § The aim of this tutorial is § Acquaint the audience with Solution of the optimization problem given above through Lagrangian Function Formulation § Explain the concepts behind duality and the Karush Kuhn Tucker (KKT) conditions § Provide practical examples 5 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Preliminaries § Concepts about the following will be used subsequently in proofs for establishing theoretical foundations for constrained optimization solution through Lagrange Function Method § Saddle Point § Convex Sets and Functions § Farkas’s Lemma 6 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Preliminaries: Saddle Point 7 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Preliminaries: Convex Sets 8 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Preliminaries: Farkas’s Lemma 9 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Constrained Optimization: Example § Assume you have access a wire of maximum length L and you are required to use the wire length to enclose a barn with rectangular area of length x 1 and width x 2 such that the enclosed area is maximum § Mathematically § Optimize the objective function § Max A=x 1 x 2 § Subject to constraints § 2(x 1+x 2)≤L 10 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Lagrangian Formulation § Lagrange proposed a method for the solution of COP § f(x) and gi(x) are convex functions § hi(x) are affine functions 11 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Lagrangian Formulation… § The solution proposed by Lagrange is based on the following unconstrained minimization § Where and properties have the following § Large penalties added when the constraints are not satisfied § Unconstrained optimization now leads to satisfaction of the constrains and then optimization of the original objective function 12 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Lagrangian Formulation… § One possible way of achieving the above mentioned properties for the two penalty functions is as follows When the constraint is violated (gi(x)>0) the maximization with respect to αi leads to infinity as long as αi is non-negative When the constraint is not violated the maximization with respect to αi leads to zero as long as αi is non-negative 13 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Lagrangian Formulation… § Thus we can write the optimization problem as § αi and βi are called Lagrange multipliers (or dual variables) and the function (below) is called the Lagrange Function 14 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Lagrangian function: Barn example § The problem can be rewritten as § Min f(x) = -x 1 x 2 § Subject to constraints § 2(x 1+x 2) ≤ L, OR § g(x) = 2(x 1+x 2) – L ≤ 0 § This implies 15 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Lagrangian function: Barn example… § This can be solved as 16 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Key Question! § We now look for a mathematical proof that the optimization of the Lagrangian function does lead to the constrained optimization of the original objective function § Thus the question we are asking is: § How is the Lagrangian Formulation related to the original COP? § To answer the question we introduce the notions of primal and dual problems associated with a Lagrangian Function 17 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Primal Problem § Consider the optimization problem Primal Objective Function § Primal Feasibility § A point x is said to be primal feasible if § Primal Optimality § Let x* indicate the solution of primal problem with 18 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Dual Problem § Consider the optimization problem Dual Objective Function § Dual Feasibility § (α, β) is said to be primal feasible if § Dual Optimality § Let (α*, β*) indicate the solution of dual problem with 19 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Barn Example § Primal § Dual 20 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Saddle Point of Lagrangian Function § The saddle point of L(x, α, β) is defined as a tuple (x*, α*, β*) such that L(x, α*, β*) L(x, α, β) L(x*, α*, β*) L(x*, α, β) x α, β © 2008, Fayyaz A. Afsar, DCIS, PIEAS. 21

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Example 22 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Existence of Saddle Point & Feasibility § Now as 23 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Existence of Saddle Point & Feasibility… § Since A saddle point (x*, α*, β*) exists (x*, α*, β*) are feasible 24 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Complementary Slackness 25 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). The KKT 26 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Summary (Till Now) § We have proven that A saddle point (x*, α*, β*) exists (x*, α*, β*) are feasible (x*, α*, β*) satisfies KKT 27 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Saddle Point and Minimization of f(x) 28 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Summary (Till Now) § We have proven that x* is a minimizer of f(x) A saddle point (x*, α*, β*) exists (x*, α*, β*) are feasible (x*, α*, β*) satisfies KKT 29 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Existence of Saddle Point § When will a saddle point of L(x, α, β) always exist? § If a function is convex then its saddle point must exist § Therefore if L(x, α, β) is convex then a saddle point must exist § L(x, α, β) is convex when § f(x) is convex § gi(x) are convex § hi(x) are affine 30 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

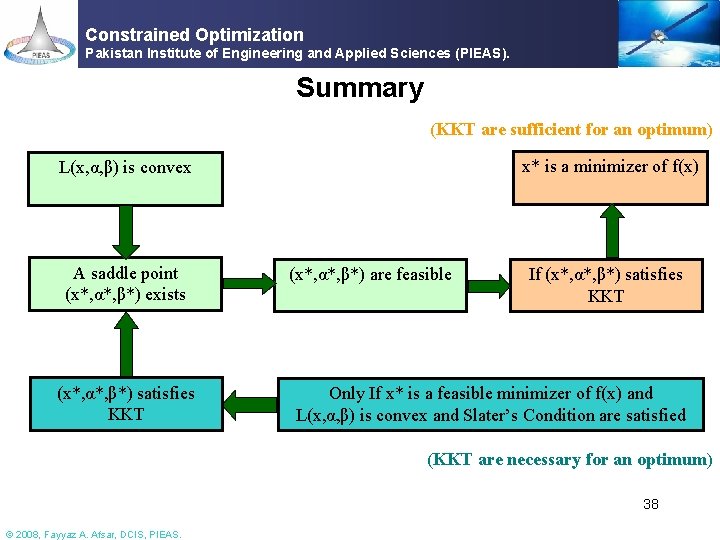
Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Summary (till now) x* is a minimizer of f(x) L(x, α, β) is convex A saddle point (x*, α*, β*) exists (x*, α*, β*) are feasible (x*, α*, β*) satisfies KKT § KKT are sufficient for finding the minimizer of the COP 31 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Proof of KKT as necessary conditions § Key Question § Is the following statement true? § If an optimal point exists then it must satisfy the KKT. § OR § It is necessary for an optimal point to satisfy the KKT. 32 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Proof of KKT as necessary conditions § Let x* be the optimal solution the system § Is infeasible (has no solution). 33 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). KKT as necessary conditions : Farkas Lemma § Assume that the Slater Condition is satisfied, then the inequality system § Has no solution, iff 34 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). KKT as necessary conditions § Taking x=x* 35 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). KKT as necessary conditions § Thus (x*, α*, β*) is a saddle point 36 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). KKT as necessary conditions § If x* is a feasible minimizer of f(x) and slater’s conditions are satisfied § L(x*, α*, β*) is a saddle point § gi(x*)≤ 0 § hi(x*)=0 § αi*≥ 0 § αi*gi(x*)=0 § i. e. KKT are satisfied 37 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Summary (KKT are sufficient for an optimum) x* is a minimizer of f(x) L(x, α, β) is convex A saddle point (x*, α*, β*) exists (x*, α*, β*) satisfies KKT (x*, α*, β*) are feasible If (x*, α*, β*) satisfies KKT Only If x* is a feasible minimizer of f(x) and L(x, α, β) is convex and Slater’s Condition are satisfied (KKT are necessary for an optimum) 38 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). Conclusion § If the COP is convex and slater’s conditions are satisfied then KKT are necessary and sufficient conditions for existence of an optimum point of the original objective function at the saddle point of the Lagrangian Function. 39 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Constrained Optimization Pakistan Institute of Engineering and Applied Sciences (PIEAS). End of Presentation Like as the waves make towards the pebbled shore, So do our minutes hasten to their end. William Shakespeare (1564– 1616), English poet and playwright. Sonnet 60 (1609).