ENERGY CONVERSION ONE Course 25741 Chapter one Electromagnetic






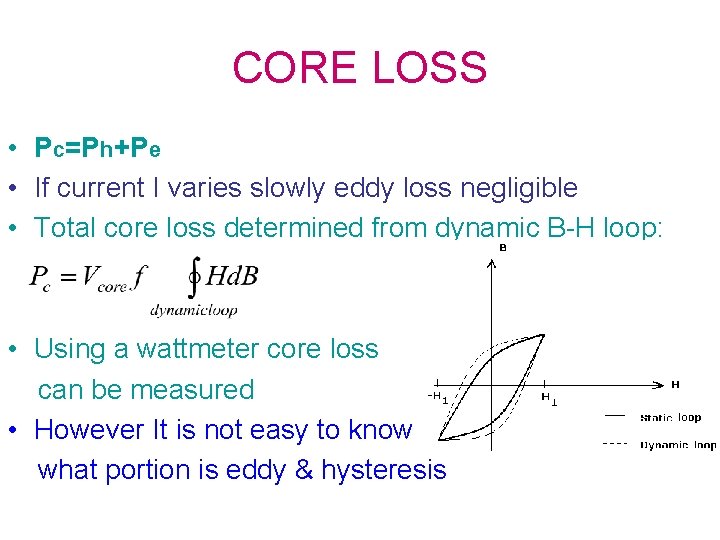












- Slides: 24

ENERGY CONVERSION ONE (Course 25741) Chapter one Electromagnetic Circuits …continued

Hysteresis Losses • As I of coil slowly varying in a coil energy flows to coil-core from source • However, Energy flowing in > Energy returns • The net energy flow from source to coil is the heat in core (assuming coil resistance negligible) • The loss due to hysteresis called : Hysteresis Loss • hysteresis loss ~ Size of hysteresis loop • Voltage e across the coil: e=N dφ/dt

Hysteresis Losses • Energy transfer during t 1 to t 2 is: • Vcore=A l, volume of core • Power loss due to hysteresis in core: Ph=Vcore Wh f • f freq. of variation of i • Steinmetz of G. E. through large no. of experiment for machine magnetic materials proposed a relation: Area of B-H loop = • Bmax is the max flux density

Hysteresis Losses • n varies from 1. 5 to 2. 5, • K is a constant • Therefore the hysteresis power loss: Ph=Kh (Bmax)^n f • Kh a constant depends on - ferromagnetic material and - core volume

EDDY CURRENT LOSS • Another power loss of mag. Core is due to rapid variation of B (using ac source) • In core cross section, voltage induced and ie passes, resistance of core cause: Pe =ie^2 R (Eddy Current loss) • this loss can be reduced as follows when: a- using high resistive core material, few % Si b- using a laminated core

EDDY CURRENT LOSS • Application of Laminated Core Eddy current loss: Pe=Ke. Bmax^2 f^2 Ke: constant depends on material & lamination thickness which varies from 0. 01 to 0. 5 mm
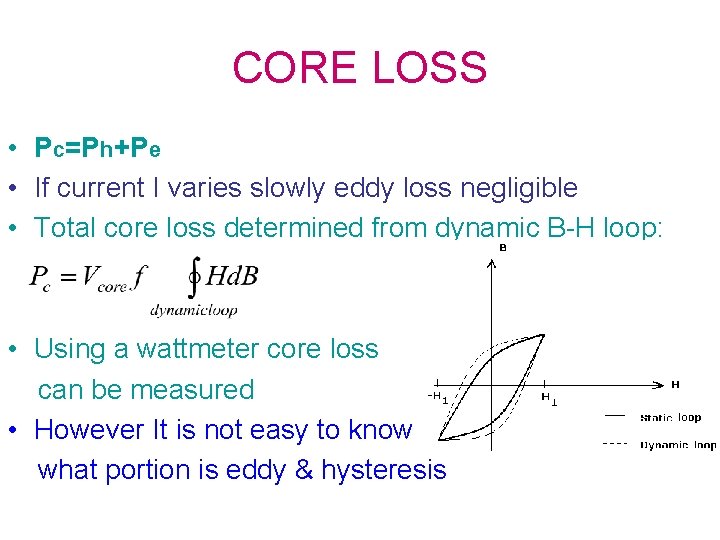
CORE LOSS • Pc=Ph+Pe • If current I varies slowly eddy loss negligible • Total core loss determined from dynamic B-H loop: • Using a wattmeter core loss can be measured • However It is not easy to know what portion is eddy & hysteresis

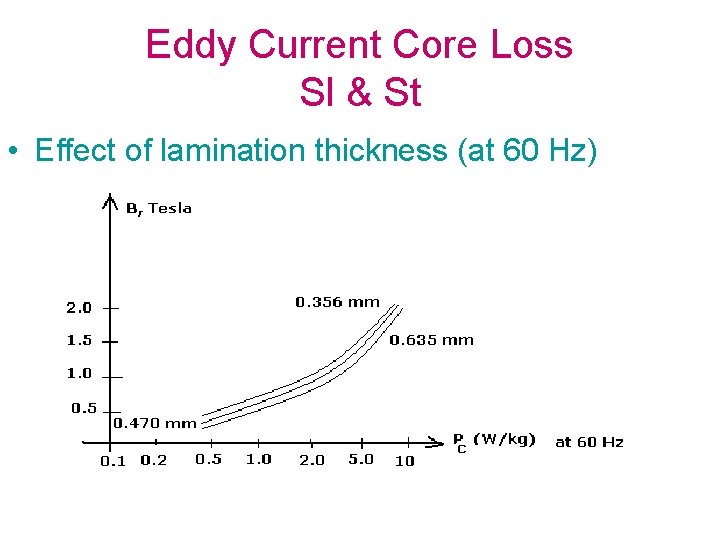
Eddy Current Core Loss Sl & St • Effect of lamination thickness (at 60 Hz)

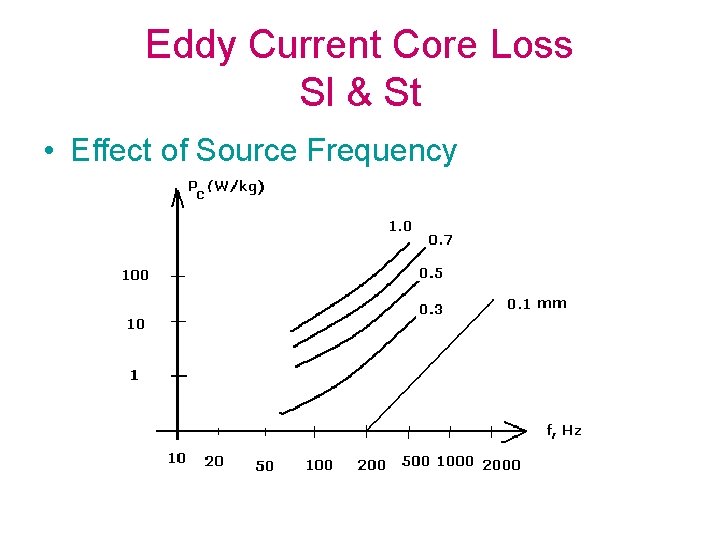
Eddy Current Core Loss Sl & St • Effect of Source Frequency

Sinusoidal Excitation • Example: • A square wave voltage E=100 V & f=60 Hz applied coil on a closed iron core, N=500 • Cross section area 0. 001 mm^2, assume coil has no resistance • a- max value of flux & sketch V & φ vs time • b- max value of E if B<1. 2 Tesla

Sinusoidal Excitation • • a - e = N dφ/dt => N. ∆φ=E. ∆t E constant => 500(2φmax)=Ex 1/120 Φmax=100/(1000 x 120)Wb=0. 833 x 10^-3 Wb b - Bmax=1. 2 T (to find maximum value of E) Φmax=Bmax x A=1. 2 x 0. 001=1. 2 x 10^-3 Wb N(2φmax)=E x 1/120 Emax =120 x 500 x 2 x 10^-3=144 V

Exciting Current Using ac Excitation • Current which establish the flux in the core • The term : Iφ if B-H nonlinear, nonsinusoid • a - ignoring Hysteresis: • B-H curve Ξ φ-i curve (or the rescaled one) • Knowing sine shape flux, exciting current waveform by help of φ-i curve obtained • The current non-sinusoidal, iφ1 lags V 90° no loss (since Hysteresis neglected)

Exciting Current • Realizing Hysteresis, Exciting Current recalculated • Now iφ determined from multi-valued φ-I curve • Exciting current nonsinusoid & nonsymmetric • It can split to 2 components: ic in phase with e (represents loss), im in ph. With φ & symmetric

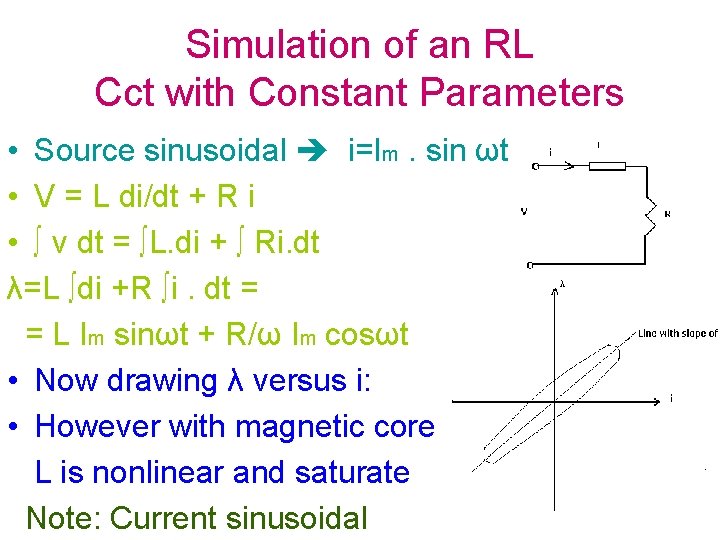
Simulation of an RL Cct with Constant Parameters • Source sinusoidal i=Im. sin ωt • V = L di/dt + R i • ∫ v dt = ∫L. di + ∫ Ri. dt λ=L ∫di +R ∫i. dt = = L Im sinωt + R/ω Im cosωt • Now drawing λ versus i: • However with magnetic core L is nonlinear and saturate Note: Current sinusoidal

Wave Shape of Exciting Current a- ignoring hysteresis • From sinusoidal flux wave & φ-i curve for mag. System with ferromagnetic core, iφ determined • iφ as expected nonsinusoidal & in phase with φ and symmetric w. r. t. to e • Fundamental component iφ1 of exciting current lags voltage e by 90◦ (no loss) • Φ-i saturation characteristic & exciting current

Wave Shape of Exciting Current b- Realizing hysteresis • Hysteresis loop of magnetic system with ferromagnetic core considered • Waveform of exciting current obtained from sinusoidal flux waveform &multivalued φ-i curve • Exciting current nonsinusoidal & nonsymmetric

Wave Shape of Exciting Current • It can be presented by summation of a series of harmonics of fundamental power frequency • ie = ie 1 + ie 3 + ie 5 +… A • It can be shown that main components are the fundamental & the third harmonic

Equivalent Circuit of an Inductor • Inductor: is a winding around a closed magnetic core of any shape without air gap or with air gap • To build a mathematical model we need realistic assumptions to simplify the model as required, and follow the next steps: • Build a System Physical Image • Writing Mathematical Equations

Equivalent Circuit of an Inductor • Assumptions for modeling an Ideal Inductor: 1 - Electrical Fields produced by winding can be ignored 2 - Winding resistance can be ignored 3 - Magnetic Flux confined to magnetic core 4 - Relative magnetic permeability of core material is constant 5 - Core losses are negligible

Equivalent Circuit of an Inductor Ideal Inductor • • • v = e = dλ / dt Volts λ = L ie Wb v = L d ie /dt Volts realizing winding resistance in practice v = L d ie /dt + Rw ie Volts

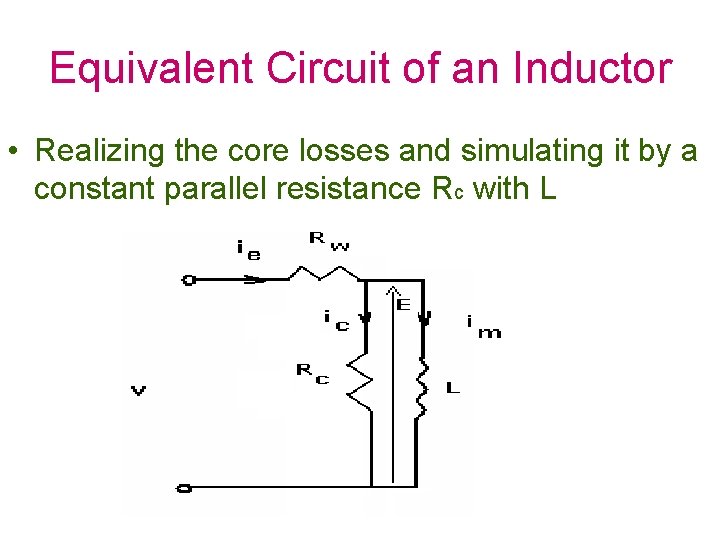
Equivalent Circuit of an Inductor • Realizing the core losses and simulating it by a constant parallel resistance Rc with L

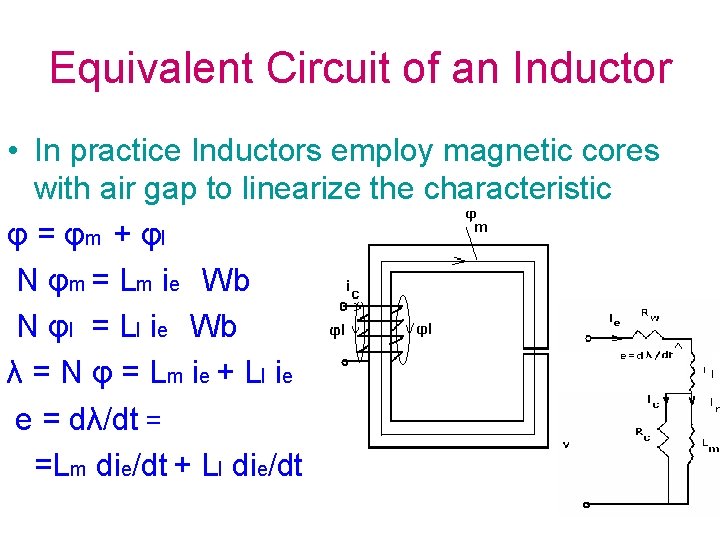
Equivalent Circuit of an Inductor • In practice Inductors employ magnetic cores with air gap to linearize the characteristic φ = φm + φl N φm = Lm ie Wb N φl = Ll ie Wb λ = N φ = L m ie + Ll ie e = dλ/dt = =Lm die/dt + Ll die/dt

Equivalent Circuit of an Inductor • Example: A inductor with air gap in its magnetic core has N=2000, and resistance of Rw=17. 5 Ω. When ie passes the inductor a measurement search coil in air gap measures a flux of 4. 8 m. Wb, while a search coil close to inductor’s winding measures a flux of 5. 4 m. Wb • Ignoring the core losses determine the equivalent circuit parameters

Equivalent Circuit of an Inductor • • φ = 5. 4 m. Wb, φm= 4. 8 m. Wb φl= φ – φm =0. 6 m. Wb Lm=N φm/ ie =2000 x 4. 8/0. 7=13. 7 H Ll=N φl/ ie = 2000 x 0. 6 / 0. 7=1. 71 H
 Energy conversion means saving energy
Energy conversion means saving energy Electromagnetic energy def
Electromagnetic energy def Energy density of electromagnetic wave
Energy density of electromagnetic wave Em waves formulas
Em waves formulas Electromagnetic waves obey principle of .. *
Electromagnetic waves obey principle of .. * Energy carried by electromagnetic waves
Energy carried by electromagnetic waves Spectre électromagnétique
Spectre électromagnétique Energy density of electromagnetic wave
Energy density of electromagnetic wave Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Half brick wall
Half brick wall Course title and course number
Course title and course number Course interne moyenne externe
Course interne moyenne externe Classification of winds
Classification of winds Michael faraday
Michael faraday Blender energy transformation
Blender energy transformation Microwave oven energy transformation
Microwave oven energy transformation Energy conversion and conservation
Energy conversion and conservation Example of electrical energy
Example of electrical energy Alarm clock energy conversion
Alarm clock energy conversion Transformer energy conversion
Transformer energy conversion Energy conversion table
Energy conversion table Energy meaning in science
Energy meaning in science Electrical to thermal
Electrical to thermal Windmill energy conversion
Windmill energy conversion