Efficient Topk Queries in LargeScale Networks Pei Cao

Efficient Top-k Queries in Large-Scale Networks Pei Cao Cisco Systems, Inc. Consulting Faculty, Stanford University

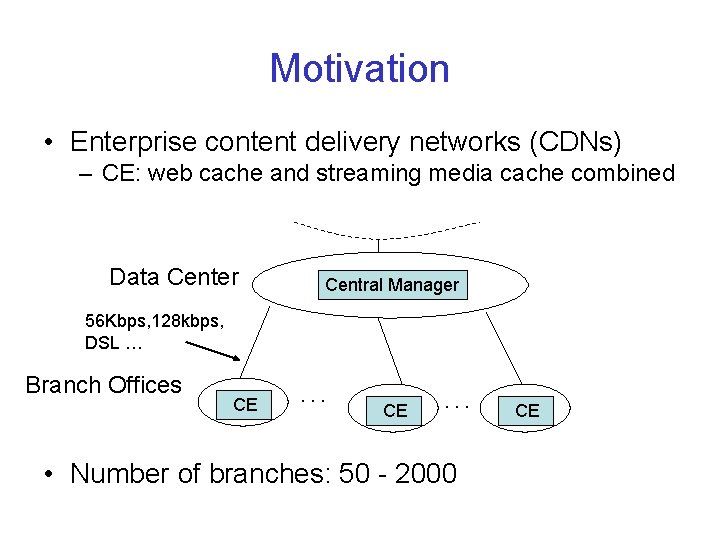
Motivation • Enterprise content delivery networks (CDNs) – CE: web cache and streaming media cache combined Data Center Central Manager 56 Kbps, 128 kbps, DSL … Branch Offices CE . . . • Number of branches: 50 - 2000 CE

Top-k Queries in CDNs Example queries: • Across all CEs, which URLs are accessed most often? • Across all CEs, which domains consume the most storage? • Across all CEs, which cached objects produced the biggest bandwidth savings? • etc.

Definitions • a network of m nodes, connected to a central manager (CM) • each node i has a reverse-sorted list of ( x, Vi(x) ) • an object’s sum V(x) = V 1(x)+V 2(x)+…+Vm(x) • Problem: find the k objects with highest sums • Goal: answer this question with minimum network traffic A generic problem in distributed systems

Existing Methods • “Naïve” Algorithm – Each node sends the full list of objects and their values to the Central Manager • Threshold Algorithm (TA) – Proposed by multiple groups in the database research community

The Threshold Algorithm (TA) • Example: find top 2 objects with max sums in three columns Node 1 (A, 10) (C, 8) (E, 8) (F, 8) (B, 7) (D, 5) (J, 1) (K, 1). . . Node 2 (B, 10) (D, 9) (F, 8) (H, 6) (G, 5) (C, 1) (A, 1) Node 3 (C, 10) (A, 9) (G, 8) (J, 7) (F, 6) (D, 4) (B, 1) . . . Central Manager (CM) T = 30; T = 26; T = 24; T = 21; T = 18; V(A)=20, V(C)=19, V(B)=18 V(A)=20, V(C)=19, … V(F)=22, V(A)=20, …

Adapting TA for Distributed Environments • Consists of multiple “rounds”, each round having two round trips – Round-trip #1 “sorted access”: CM asks for the next B objects on the lists and nodes respond – Round-trip #2 “random lookup”: CM sends a list of object names to nodes and nodes supply values – B=k • Issues – # of rounds unpredictable – O(m 2) network traffic

New Algorithm: Three-Phase Uniform Threshold (TPUT) • • Motivation: terminate in a fixed number of round trips regardless of input Operates in three phases 1. Lower-bound estimation 2. Pruning 3. Final lookup

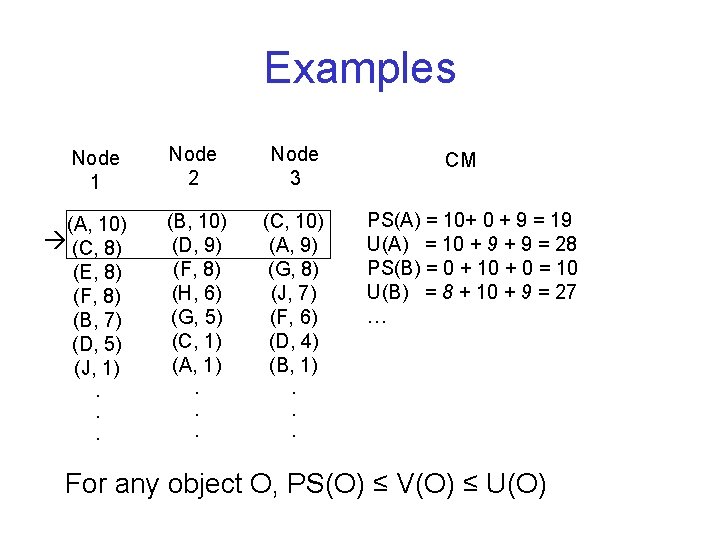
Partial Sums and Upper Bounds • Partial sum: PS(x) = ∑Vi’(x) = Vi(x), if x has been reported by node i to CM 0, otherwise • Upper bound: U(x) = ∑Ui’(x) = Vi(x), if x has been reported by node i to CM Ti, otherwise Ti: Node i sends all objects with values > Ti

Examples Node 1 (A, 10) (C, 8) (E, 8) (F, 8) (B, 7) (D, 5) (J, 1). . . Node 2 Node 3 (B, 10) (D, 9) (F, 8) (H, 6) (G, 5) (C, 1) (A, 1) (C, 10) (A, 9) (G, 8) (J, 7) (F, 6) (D, 4) (B, 1) . . . CM PS(A) = 10+ 0 + 9 = 19 U(A) = 10 + 9 = 28 PS(B) = 0 + 10 + 0 = 10 U(B) = 8 + 10 + 9 = 27 … For any object O, PS(O) ≤ V(O) ≤ U(O)

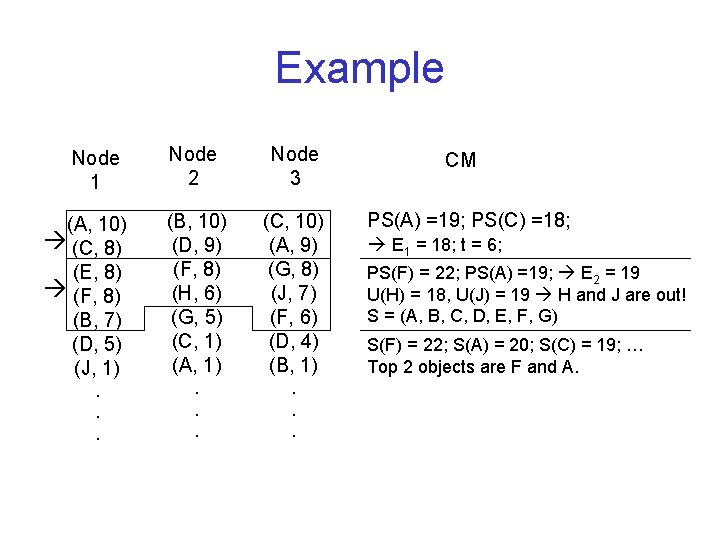
Steps in TPUT Phase 1: • Manager Nodes: start top-k query • Nodes Manager: here are my top-k objects; • Manager: – Calculate partial sums of all objects – Take the k’th partial sum E 1 (E 1 ≤E); set t = E 1/m Phase 2: • Manager Nodes: send me all objects with value ≥ t • Nodes Manager: here they are • Manager: – Calculate partial sums again; take the k’th partial sum E 2 (E 1 ≤ E 2 ≤ E) – Calculate upper bounds of all objects – S = {objects whose upper bounds are ≥ E 2} Phase 3: • Manager Nodes: here is S; send me all objects in S • Nodes Manager: here they are

Example Node 1 (A, 10) (C, 8) (E, 8) (F, 8) (B, 7) (D, 5) (J, 1). . . Node 2 Node 3 (B, 10) (D, 9) (F, 8) (H, 6) (G, 5) (C, 1) (A, 1) (C, 10) (A, 9) (G, 8) (J, 7) (F, 6) (D, 4) (B, 1) . . . CM PS(A) =19; PS(C) =18; E 1 = 18; t = 6; PS(F) = 22; PS(A) =19; E 2 = 19 U(H) = 18, U(J) = 19 H and J are out! S = (A, B, C, D, E, F, G) S(F) = 22; S(A) = 20; S(C) = 19; … Top 2 objects are F and A.

Improving the Pruning Power • Set t = (E 1/m) * α, where 0<α<1 U(o) Node 1 Node 2 (x 1, . . . ) (x 2, …) (y 1, …) (y 2, …) (z 1, . . . ) (z 2, . . . ) . . . . Node n E 2/m t

Compression via Hashing • Problem: object IDs can be too long • Solution: send hashed keys of object IDs – – Node report to CM (hash(o), V(o)) If hash(o 1)==hash(o 2), then V = max(V(o 1), V(o 2)) Candidate set S is a set of hashed keys Size of key = log(total # of objects in all nodes) • Effect: – Algorithm is still correct – However, might need an additional round trip

Evaluating TPUT Algorithm • Trace-driven simulation • Optimality analysis

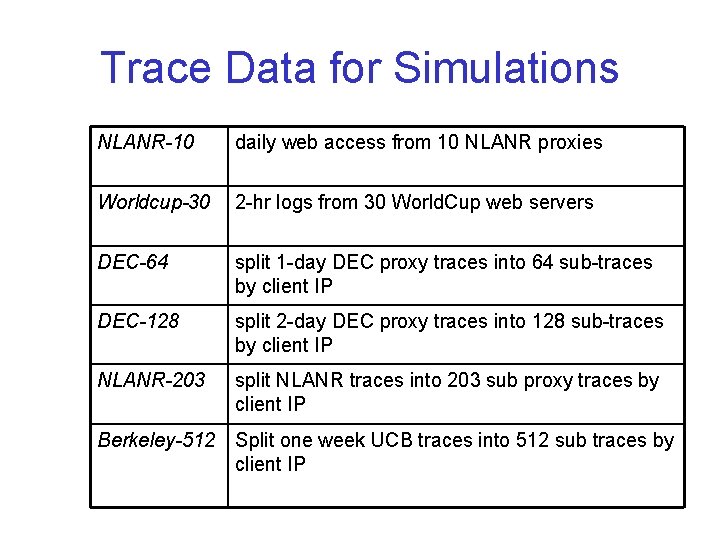
Trace Data for Simulations NLANR-10 daily web access from 10 NLANR proxies Worldcup-30 2 -hr logs from 30 World. Cup web servers DEC-64 split 1 -day DEC proxy traces into 64 sub-traces by client IP DEC-128 split 2 -day DEC proxy traces into 128 sub-traces by client IP NLANR-203 split NLANR traces into 203 sub proxy traces by client IP Berkeley-512 Split one week UCB traces into 512 sub traces by client IP

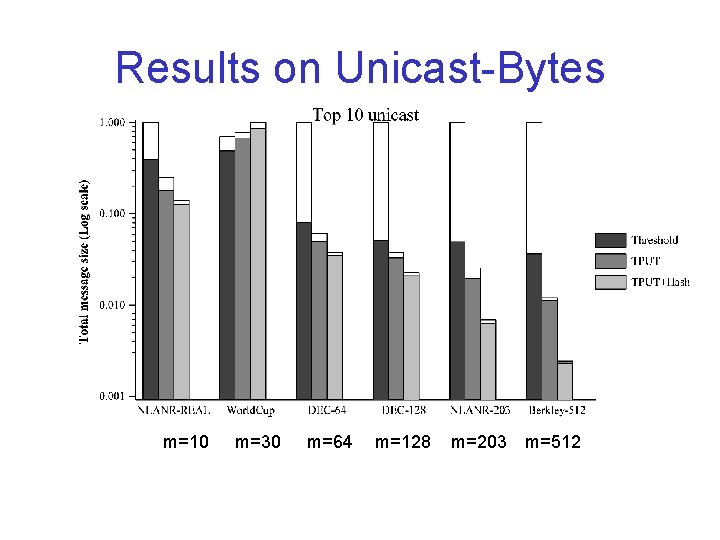
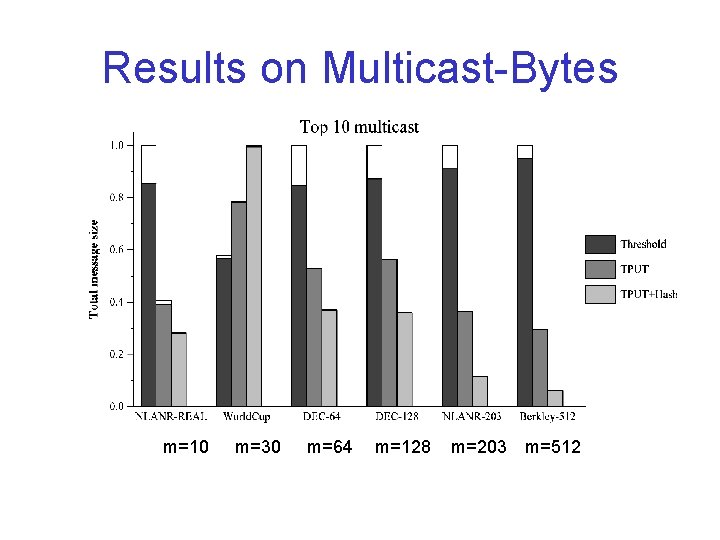
Performance Metrics • Communication costs – Unicast-bytes – Multicast-bytes – Messages are all compressed by gzip

Results on Unicast-Bytes m=10 m=30 m=64 m=128 m=203 m=512

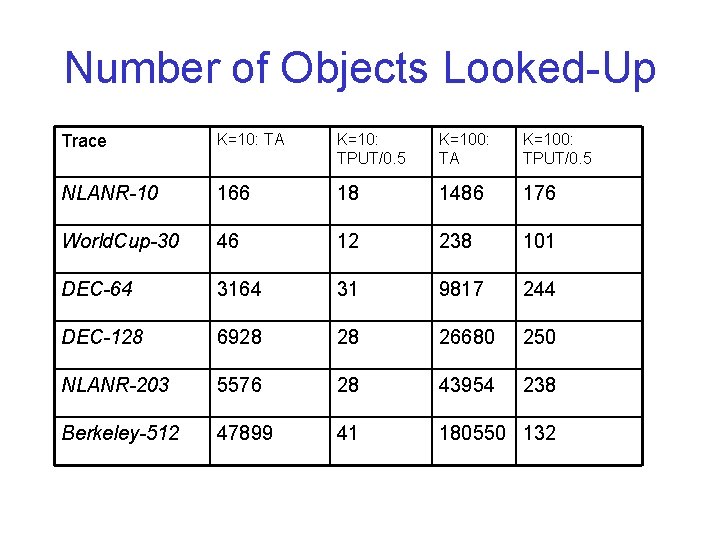
Number of Objects Looked-Up Trace K=10: TA K=10: TPUT/0. 5 K=100: TA K=100: TPUT/0. 5 NLANR-10 166 18 1486 176 World. Cup-30 46 12 238 101 DEC-64 31 9817 244 DEC-128 6928 28 26680 250 NLANR-203 5576 28 43954 238 Berkeley-512 47899 41 180550 132

Results on Multicast-Bytes m=10 m=30 m=64 m=128 m=203 m=512

Optimality Analysis Main results: • TPUT is instance optimal for data sets with a log-log slope function C(n) – Zipf distribution: C(n) = n – Zipf distribution: opt-ratio = (m-1)*2 m +k*m • Setting α<1 reduces cost qualitatively. – Zipf distribution: opt-ratio = (m-1) O(√m ) +k*m/α

General Instance Optimality • Definition: An algorithm R is instance-optimal with optimality ratio C 1, if exists C 2, such that for any data series D, and any algorithm A, cost(R, D) ≤ C 1 * cost(A, D) + C 2 – cost is amount of network traffic – TA is instance optimal with opt-ratio = O(m 2)

Worst Cases for Fixed Number Round-Trip Algorithms Finding obj with highest sum Node 1 (A, 1) (C, 1) (X 1, 0. 6) (X 2, 0. 6). . . (Xn, 0. 6) (B, 0. 5). . Node 2 (B, 1) (D, 0. 2). . • TPUT is not general instance optimal • Nor can any algorithm that terminates in a fixed number of round trips regardless of input

Log-Log Slope Function List Position 1. . . Position j*C(n). . . . L(j) < L(j)/n • L(j) is the value at position j in a reversesorted list • The list satisfies loglog slope function C(n), if, for all j≤k, L(j*C(n)) < L(j)/n • For Zipf-like distribution L(j) ~ 1/jλ, C(n) = n 1/λ.

Properties of the Two Lower Bounds • Let E be the “true bottom” • E 1 ≥ E/m • E 2 > E/2 – E 2 ≥ E 1 – E 2 > E – E 1*(m-1)/m • For any x, V(x) – PS(x) < (m-1)*t V(x) – PS(x) < (m-1) * E 1/m E – E 2 < E 1 * (m-1)/m – E 2 > (m/(2 m-1))*E

Restricted Instance Optimality of TPUT (α=1) • Assume D is a collection of m lists all following log-log slope function C(n), then for any algorithm A, cost(TPUT, D) ≤ cost(A, D) * ((m-1)*C(2 m) + C(m)*k) – Proof: assume the optimal algorithm for D stops at position bi on list i, then L(bi) < E; • The number of objects in S from node i is ≤ bi * C(2 m) • Each node sends ≤ C(m) * k objects in round-trip #2

Effect of α<1 • Property: – If object x appears in n nodes in Phase 2 and U(x)≥ E 2, then its average value in those nodes R(x) ≥ E 2 * (1 -α)/n • Let li = the num of objects in S that appear in exactly i nodes in Phase 2, then: – 1*l 1 + 2*l 2 + 3*l 3 + … + m*lm ≤ C(m * (1+α)/α) * ∑bi – l 1 + l 2 + … + li ≤ C( i * (1+ α)/(1 -α)) * ∑bi – Size of S is l 1 + l 2 + … + lm

Analysis of α<1 • What’s the maximum l 1+l 2+ … +lm under the following constraints? – 1*l 1+2*l 2 + 3*l 3 + … + m*lm ≤ C(m * (1+α)/α) * B – l 1 ≤ C(1*β) *B – l 1+l 2 ≤ C(2*β) *B –. . . – l 1+l 2+ … +lm ≤ C( m * β) *B where β = (1+α)/(1 -α), B= ∑bi • Solution: maximize l 1, l 2, …, ld, and set ld+1, ld+2, …, lm to 0 – Li = C(i* β) *B – C((i-1)* β) *B – d * C(d* β) *B - ∑C(i* β) *B ≤ C(m * (1+α)/α) * B – Candidate set size S = C(d * β) *B

α For Zipf Distributions • For Zipf distribution, where C(n) = n, size of candidate set S is c*√m * B Optimality ratio for TPUT with α<1 is (m-1) * c * √m + m/α *k

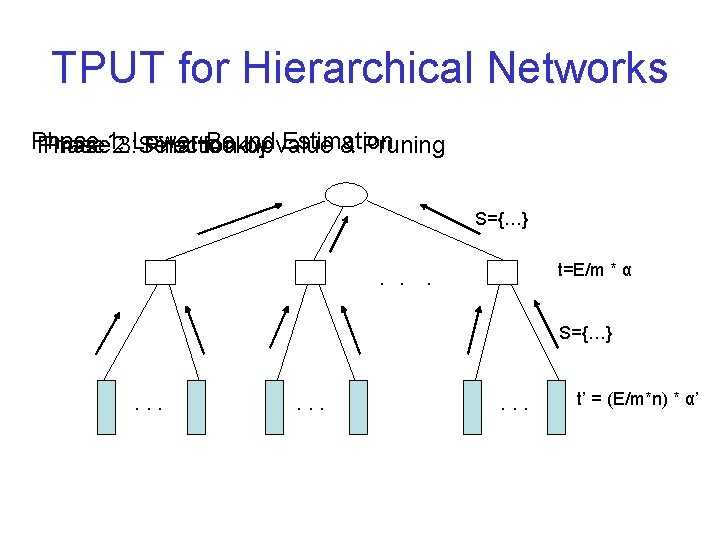
TPUT for Hierarchical Networks Phase Estimation Phase 1: 2: 3: Lower-Bound Selection Final lookup by value & Pruning S={…} t=E/m * α . . . S={…} . . t’ = (E/m*n) * α’

Summary and Future Work • TPUT should be used for top-k queries in distributed networks – TPUT is instance-optimal under the log-log slope function assumption – Introducing α<1 improves performance significantly • Future work: – Evaluating TPUT for hierarchical and P 2 P networks – Distributed algorithms for other aggregate statistics

Backup Slides

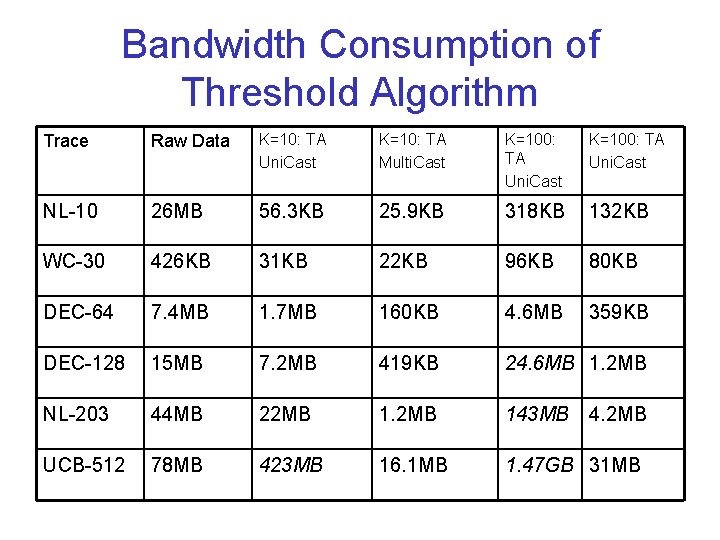
Bandwidth Consumption of Threshold Algorithm Trace Raw Data K=10: TA Uni. Cast K=10: TA Multi. Cast K=100: TA Uni. Cast NL-10 26 MB 56. 3 KB 25. 9 KB 318 KB 132 KB WC-30 426 KB 31 KB 22 KB 96 KB 80 KB DEC-64 7. 4 MB 1. 7 MB 160 KB 4. 6 MB 359 KB DEC-128 15 MB 7. 2 MB 419 KB 24. 6 MB 1. 2 MB NL-203 44 MB 22 MB 143 MB UCB-512 78 MB 423 MB 16. 1 MB 1. 47 GB 31 MB 4. 2 MB

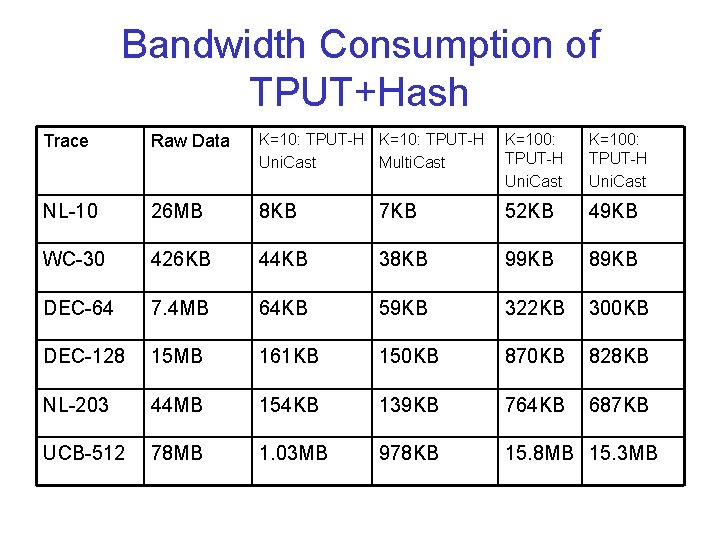
Bandwidth Consumption of TPUT+Hash Trace Raw Data K=10: TPUT-H Uni. Cast Multi. Cast K=100: TPUT-H Uni. Cast NL-10 26 MB 8 KB 7 KB 52 KB 49 KB WC-30 426 KB 44 KB 38 KB 99 KB 89 KB DEC-64 7. 4 MB 64 KB 59 KB 322 KB 300 KB DEC-128 15 MB 161 KB 150 KB 870 KB 828 KB NL-203 44 MB 154 KB 139 KB 764 KB 687 KB UCB-512 78 MB 1. 03 MB 978 KB 15. 8 MB 15. 3 MB

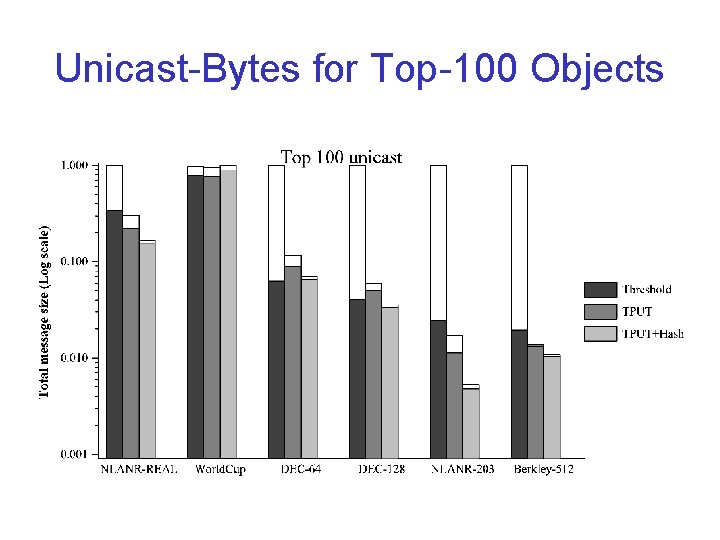
Unicast-Bytes for Top-100 Objects

Multicast-Bytes for Top-100 Objects

Varying α

Fixed-Number Round Trip Algorithms • Criteria by which a node decides to send objects: – By position – By name – By value • Any fixed-number round trip algorithm must include a “by value” operation • Any algorithm, if include “by value” operation, won’t be instance optimal

TA Running over Networks Node 1 (A, 10) (C, 8) (E, 8) (F, 8) (B, 7) (D, 5) (J, 1). . . Node 2 Node 3 (B, 10) (D, 9) (F, 8) (H, 6) (G, 5) (C, 1) (A, 1) (C, 10) (A, 9) (G, 8) (J, 7) (F, 6) (D, 4) (B, 1) . . . CM T = 26; looks up A, B, C, D V(A)=20, V(C)=19; can’t stop T = 21; looks up E, F, G, H, J V(F)=22, V(A)=20; can’t stop T = 10; stop

TPUT Phase 3: • Manager Nodes: here is S; send me all objects in S • Nodes Manager: here they are • Manager: calculate sums for objects in S; select the top k objects