EE 4780 Introduction to Computer Vision Linear Systems

Review: Linear Systems n We define a system as a unit that converts an

Linear Systems n Let where fi(x) is an arbitrary input in the class of

Linear Systems n The system H is called shift invariant if for all fi(x)

Linear Systems n The operator H is said to be causal, and hence the

Linear Systems n A unit impulse function, denoted (a), is defined by the expression

Linear Systems n The response of a system to a unit impulse function is

Linear Systems n If H is a linear shift-invariant system, then we can find

Linear Systems n Convolution of two functions is defined as n In the discrete

Linear Systems n In the 2 D discrete case is a linear filter. Bahadir

Convolution Example h 1 -1 -1 1 2 -1 1 Rotate 1 1 1

Convolution Example -1 2 1 Step 1 1 -1 1 1 h 1 1

Convolution Example -1 2 1 Step 2 1 -1 1 1 h 1 1

Convolution Example -1 2 1 Step 3 1 -1 1 1 h 1 1

Convolution Example -1 2 1 Step 4 1 -1 1 1 h 1 1

Convolution Example -1 2 1 Step 5 1 -1 1 1 h 1 2

Convolution Example -1 2 1 Step 6 1 -1 1 1 h 2 2

Convolution Example and so on… From C. Rasmussen, U. of Delaware Bahadir K. Gunturk

Try MATLAB f=imread(‘saturn. tif’); figure; imshow(f); [height, width]=size(f); f 2=f(1: height/2, 1: width/2); figure;

Gaussian Lowpass Filter Bahadir K. Gunturk 22

Gaussian Lowpass Filter Original Bahadir K. Gunturk =2 =4 From Forsyth & Ponce 23

Slides: 23

Download presentation

EE 4780: Introduction to Computer Vision Linear Systems Bahadir K. Gunturk

Review: Linear Systems n We define a system as a unit that converts an input function into an output function. Independent System operator variable Bahadir K. Gunturk 2

Linear Systems n Let where fi(x) is an arbitrary input in the class of all inputs {f(x)}, and gi(x) is the corresponding output. n If Then the system H is called a linear system. n A linear system has the properties of additivity and homogeneity. Bahadir K. Gunturk 3

Linear Systems n The system H is called shift invariant if for all fi(x) {f(x)} and for all x 0. n This means that offsetting the independent variable of the input by x 0 causes the same offset in the independent variable of the output. Hence, the input-output relationship remains the same. Bahadir K. Gunturk 4

Linear Systems n The operator H is said to be causal, and hence the system described by H is a causal system, if there is no output before there is an input. In other words, n A linear system H is said to be stable if its response to any bounded input is bounded. That is, if where K and c are constants. Bahadir K. Gunturk 5

Linear Systems n A unit impulse function, denoted (a), is defined by the expression (a) (x-a) x Bahadir K. Gunturk a 6

Linear Systems n The response of a system to a unit impulse function is called the impulse response of the system. h(x) = H[ (x)] Bahadir K. Gunturk 7

Linear Systems n If H is a linear shift-invariant system, then we can find its reponse to any input signal f(x) as follows: n This expression is called the convolution integral. It states that the response of a linear, fixed-parameter system is completely characterized by the convolution of the input with the system impulse response. Bahadir K. Gunturk 8

Linear Systems n Convolution of two functions is defined as n In the discrete case Bahadir K. Gunturk 9

Linear Systems n In the 2 D discrete case is a linear filter. Bahadir K. Gunturk 10

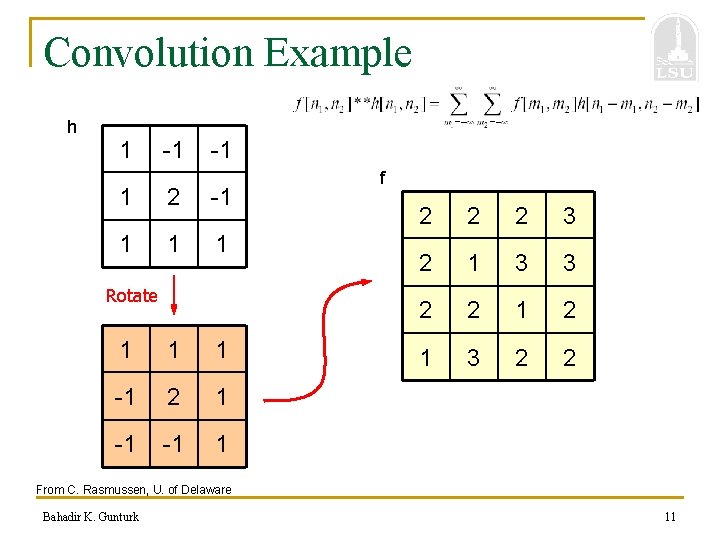
Convolution Example h 1 -1 -1 1 2 -1 1 Rotate 1 1 1 -1 2 1 -1 -1 1 f 2 2 2 3 2 1 3 3 2 2 1 3 2 2 From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 11

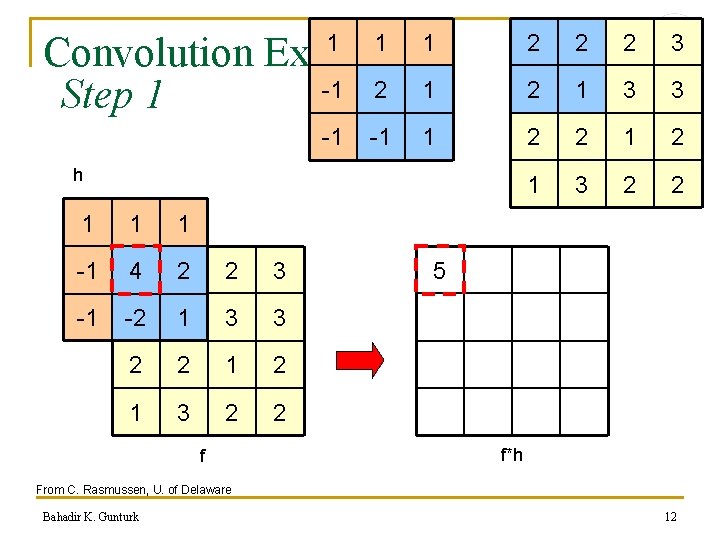
Convolution Example -1 2 1 Step 1 1 -1 1 1 h 1 1 1 -1 2 4 2 2 3 -1 2 -2 1 3 3 2 2 1 3 2 2 f 2 2 2 3 2 1 3 3 2 2 1 3 2 2 5 f*h From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 12

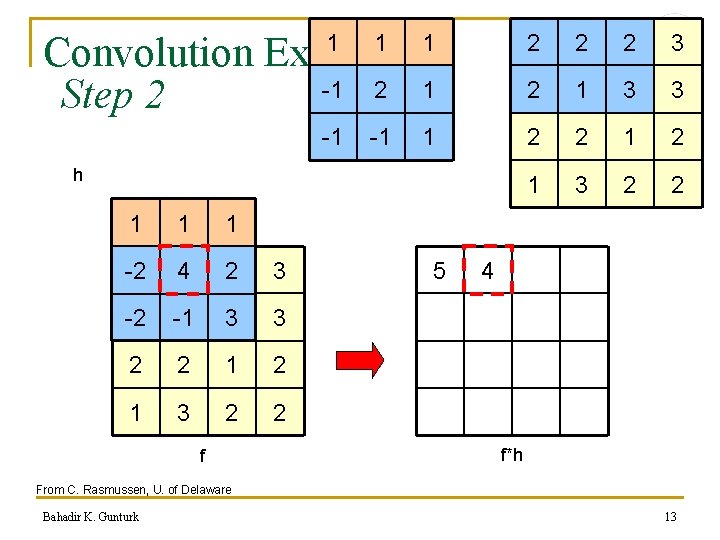
Convolution Example -1 2 1 Step 2 1 -1 1 1 h 1 1 1 2 -2 2 4 2 3 2 -2 1 -1 3 3 2 2 1 3 2 2 f 5 2 2 2 3 2 1 3 3 2 2 1 3 2 2 4 f*h From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 13

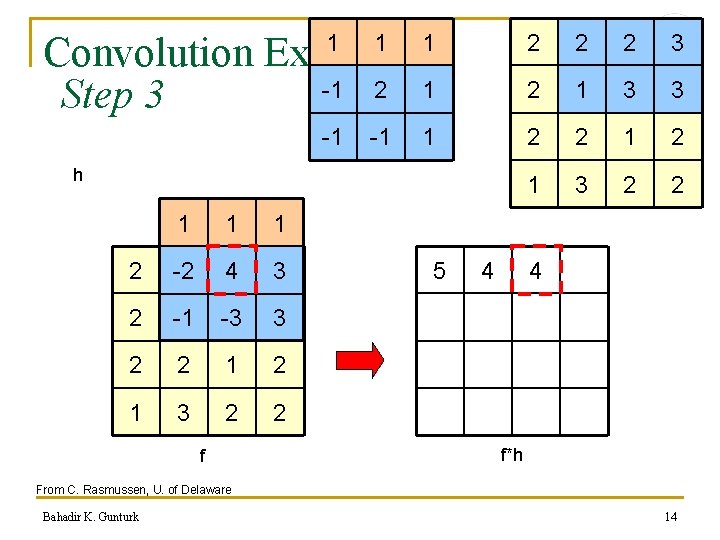
Convolution Example -1 2 1 Step 3 1 -1 1 1 h 1 1 1 2 2 -2 2 4 3 2 1 -1 3 -3 3 2 2 1 3 2 2 f 5 4 2 2 2 3 2 1 3 3 2 2 1 3 2 2 4 f*h From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 14

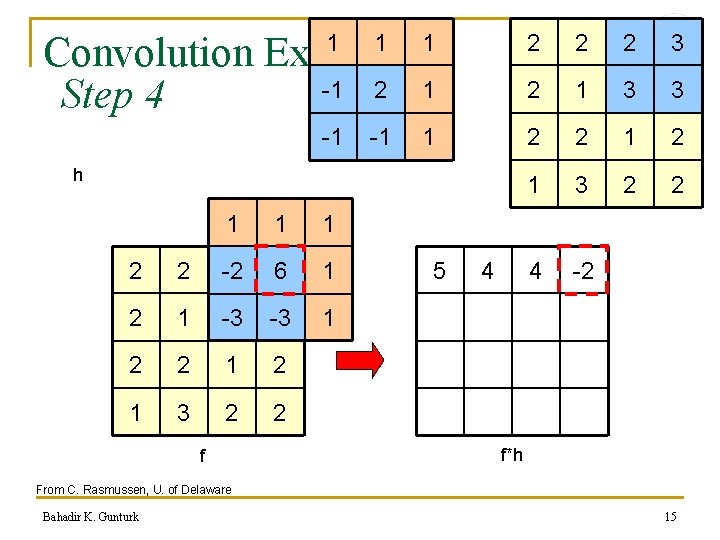
Convolution Example -1 2 1 Step 4 1 -1 1 1 h 1 1 1 2 2 2 -2 3 6 1 2 1 3 -3 1 2 2 1 3 2 2 f 5 4 2 2 2 3 2 1 3 3 2 2 1 3 2 2 4 -2 f*h From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 15

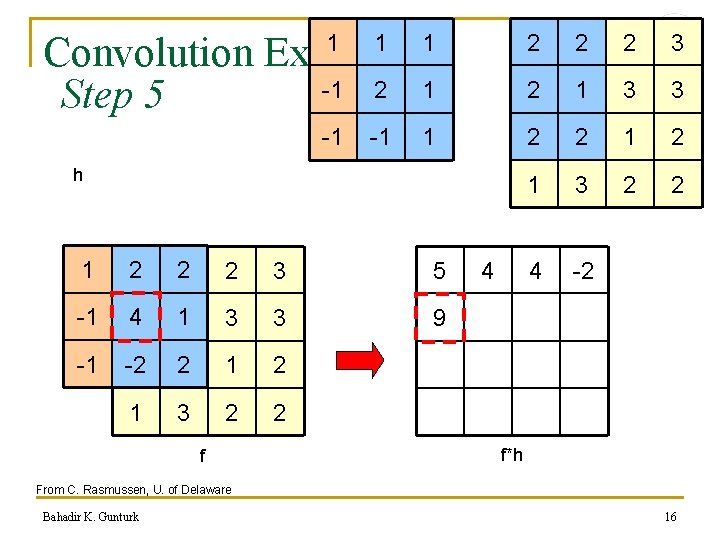
Convolution Example -1 2 1 Step 5 1 -1 1 1 h 1 2 2 2 3 5 -1 4 2 1 3 3 9 -1 -2 2 2 1 3 2 2 f 4 2 2 2 3 2 1 3 3 2 2 1 3 2 2 4 -2 f*h From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 16

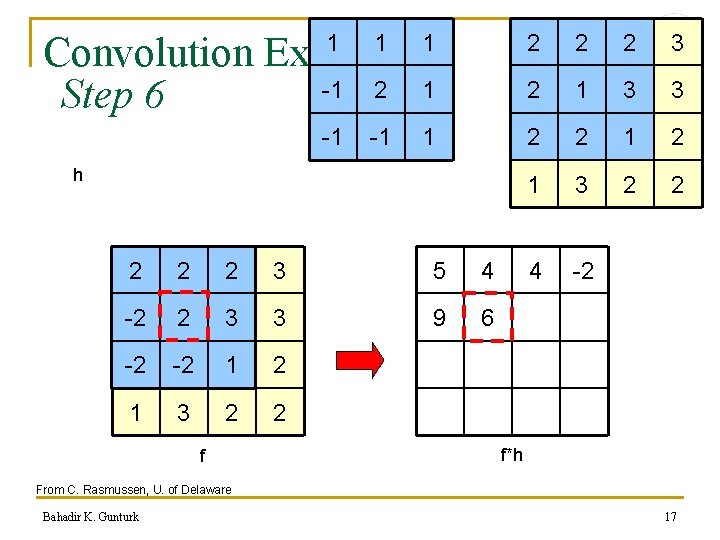
Convolution Example -1 2 1 Step 6 1 -1 1 1 h 2 2 2 3 5 4 -2 2 2 1 3 3 9 6 2 -2 1 2 1 3 2 2 f 2 2 2 3 2 1 3 3 2 2 1 3 2 2 4 -2 f*h From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 17

Convolution Example and so on… From C. Rasmussen, U. of Delaware Bahadir K. Gunturk 18

Example * Bahadir K. Gunturk = 19

Example * Bahadir K. Gunturk = 20

Try MATLAB f=imread(‘saturn. tif’); figure; imshow(f); [height, width]=size(f); f 2=f(1: height/2, 1: width/2); figure; imshow(f 2); [height 2, width 2=size(f 2); f 3=double(f 2)+30*rand(height 2, width 2); figure; imshow(uint 8(f 3)); h=[1 1 1 1; 1 1]/16; g=conv 2(f 3, h); figure; imshow(uint 8(g)); Bahadir K. Gunturk 21

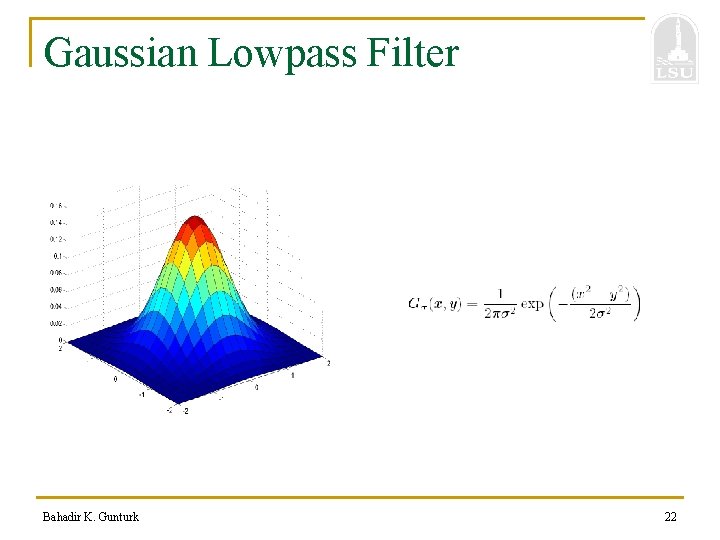
Gaussian Lowpass Filter Bahadir K. Gunturk 22

Gaussian Lowpass Filter Original Bahadir K. Gunturk =2 =4 From Forsyth & Ponce 23