Dunkle Zahlen 1 2 3 Georg Cantor 1845










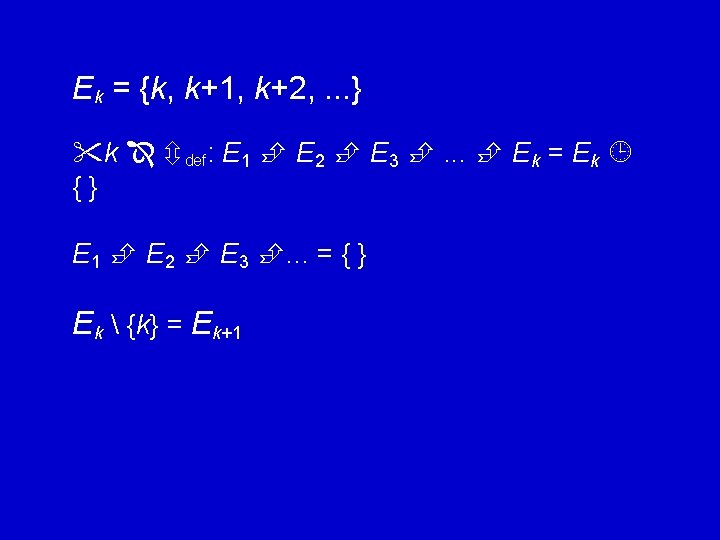


![0 [1/2, 1/1] 1 0 [1/2, 1/1] 1](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-14.jpg)
![0 [1/2, 1/1] [1/3, 1/2] 1 0 [1/2, 1/1] [1/3, 1/2] 1](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-15.jpg)
![0 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] 1 0 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] 1](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-16.jpg)
![0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n] 0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n]](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-17.jpg)
![0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n] (0, 0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n] (0,](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-18.jpg)







- Slides: 27


Dunkle Zahlen

= { 1, 2, 3, . . . } Georg Cantor (1845 - 1918) ω ist die erste ganze Zahl, die auf alle natürlichen Zahlen folgt. 1, 2, 3, 4, 5, 6, . . . , n, . . . ω ω ist die auf alle natürlichen Zahlen nächstfolgende Ordinalzahl. 1, 2, 3, 4, 5, 6, . . . , n, . . . . , ω |ω - n| = |ω| = 0


Wenn 0 Zahlen existieren, so sind sie in der letzten Spalte enthalten. Sind 0 Zahlen in der letzten Spalte enthalten, so sind sie auch im ganzen Dreieck enthalten. {1} { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } …

Wenn 0 Zahlen existieren, so sind sie in der letzten Spalte enthalten. Sind 0 Zahlen in der letzten Spalte enthalten, so sind sie auch im ganzen Dreieck enthalten. {1} { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } …

Wenn 0 Zahlen existieren, so sind sie in der letzten Spalte enthalten. Sind 0 Zahlen in der letzten Spalte enthalten, so sind sie auch im ganzen Dreieck enthalten. Zwei Zeilen enthalten niemals mehr als eine der beiden enthält. {1} { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } …

Wenn 0 Zahlen existieren, so sind sie in der letzten Spalte enthalten. Sind 0 Zahlen in der letzten Spalte enthalten, so sind sie auch im ganzen Dreieck enthalten. Zwei Zeilen enthalten niemals mehr als eine der beiden enthält. Keine Zeile enthält 0 Zahlen. {1} { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } …

Wenn 0 Zahlen existieren, so sind sie in der letzten Spalte enthalten. Sind 0 Zahlen in der letzten Spalte enthalten, so sind sie auch im ganzen Dreieck enthalten. Zwei Zeilen enthalten niemals mehr als eine der beiden enthält. Keine Zeile enthält 0 Zahlen. n def: | {1, 2, 3, . . . , n}| = 0

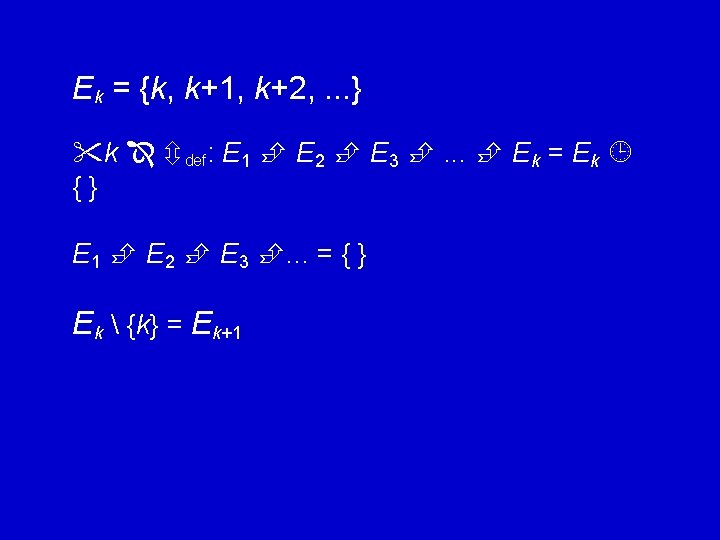
Ek = {k, k+1, k+2, . . . } k def: E 1 E 2 E 3 . . . Ek = Ek {} E 1 E 2 E 3 . . . = { } Ek {k} = Ek+1


0 1
![0 12 11 1 0 [1/2, 1/1] 1](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-14.jpg)
0 [1/2, 1/1] 1
![0 12 11 13 12 1 0 [1/2, 1/1] [1/3, 1/2] 1](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-15.jpg)
0 [1/2, 1/1] [1/3, 1/2] 1
![0 12 11 13 12 14 13 1 0 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] 1](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-16.jpg)
0 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] 1
![0 1 12 11 13 12 14 13 1n1 1n 0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n]](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-17.jpg)
0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n]
![0 1 12 11 13 12 14 13 1n1 1n 0 0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n] (0,](https://slidetodoc.com/presentation_image_h2/3c64bb612b3cb78dfe0262a21f43c069/image-18.jpg)
0 1 [1/2, 1/1] [1/3, 1/2] [1/4, 1/3] . . . [1/(n+1), 1/n] (0, 1]


Dezimaldarstellungen von Zahlen 742, 25 7 4 2 , 2 5 102 101 100 , 10 -1 10 -2 Binärdarstellungen von Zahlen 22 21 20 , 2 -1 2 -2 1 0 1 =4+0+1=5 1 1 0, 1 = 4 + 2 + 0 + 1/2 = 6, 5 0, 1 1 = 1/2 + 1/4 = 0, 75 0, 111111. . . = 1/2 + 1/4 + 1/8 +. . . = 1 0, 010101. . . = 1/4 + 1/16 + 1/64 +. . . = 1/3

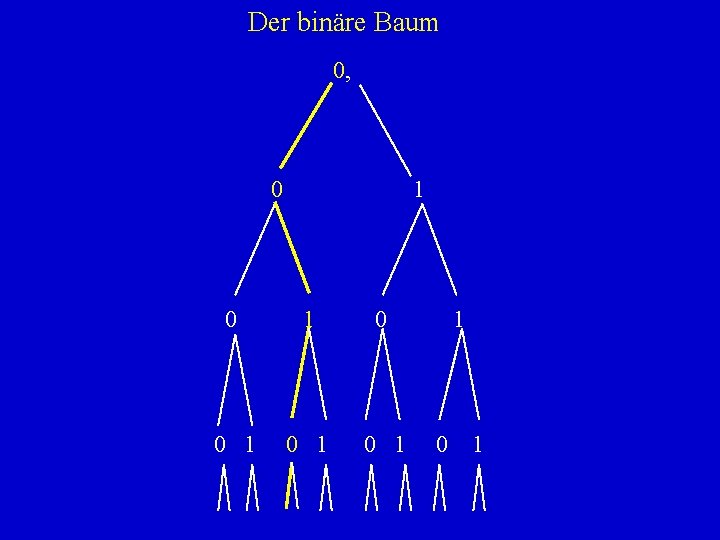
Der binäre Baum 0, 0 1 0 1 0 1

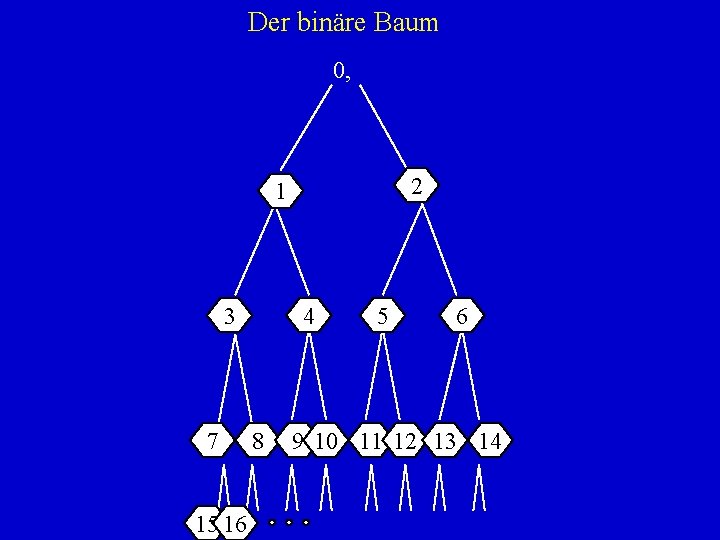
Der binäre Baum 0, 21 01 30 41 05 16 70 18 09 10 1 11 0 12 1 13 0 114 15 16

Fast alle endlichen Ordinalzahlen sind undefinierbar. 1, 2, 3, 4, 5, 6, . . . , n, . . . . , ω Damit lösen sich die Paradoxien der Mengenlehre.

Cantors erstes Diagonalverfahren Georg Cantor (1845 -1918)

Das Diagonalverfahren 0, 000111199999. . . 0, 123456789123. . . 0, 555555. . . 0, 789789. . . 0, 010030000700. . . Georg Cantor (1845 -1918)

Ausschöpfung unendlicher Mengen?

 Dr alpagut
Dr alpagut Cantor paradoksu
Cantor paradoksu Bernhard riemann biografía
Bernhard riemann biografía Texas in 1845
Texas in 1845 Republic of texas map 1845
Republic of texas map 1845 Deltapine 1845
Deltapine 1845 Dunkle nacht der seele symptome
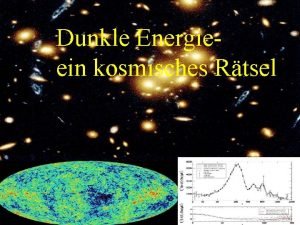
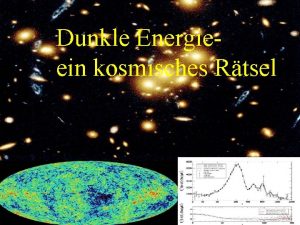
Dunkle nacht der seele symptome Dunkle energie
Dunkle energie Menschen auf dem weg durch die dunkle nacht
Menschen auf dem weg durch die dunkle nacht Kernfusion iter
Kernfusion iter Vakuumenergie dunkle energie
Vakuumenergie dunkle energie Zahlen erraten trick
Zahlen erraten trick Duale zahlensystem
Duale zahlensystem Rationale zahlen im alltag
Rationale zahlen im alltag Zahl 7 in der bibel
Zahl 7 in der bibel Blockblatt
Blockblatt Pikas zahlen unter der lupe
Pikas zahlen unter der lupe Pse zahlen bedeutung
Pse zahlen bedeutung Pikas mal plus haus
Pikas mal plus haus Römische grundzahlen
Römische grundzahlen Vier5
Vier5 013456
013456 Mathematische zaubertricks
Mathematische zaubertricks Zahlen aussprechen
Zahlen aussprechen Was sind teiler
Was sind teiler Resultatives zählen
Resultatives zählen Todaylo
Todaylo Hamburg-wechsler-intelligenztest für erwachsene
Hamburg-wechsler-intelligenztest für erwachsene