Displaying Data Dot Plots Stem and Leaf Plots













- Slides: 22

Displaying Data: § § Dot Plots Stem and Leaf Plots Grouped Frequency Tables Histograms and Bar Graphs Slide 10. 1 - 1

Graphs are used to try to tell a story. Slide 10. 1 - 2

Dot Plots A dot plot, or line plot, provides a quick and simple way of organizing numerical data. They are typically used when there is only one group of data with fewer than 50 values. Slide 10. 1 - 3

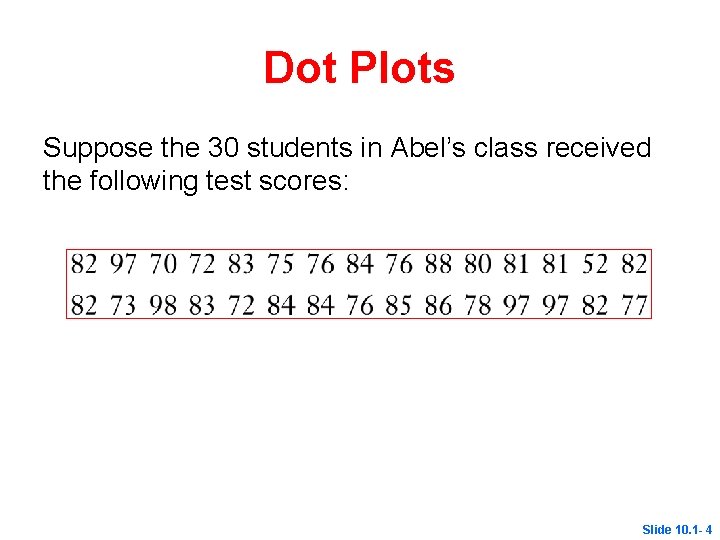
Dot Plots Suppose the 30 students in Abel’s class received the following test scores: Slide 10. 1 - 4

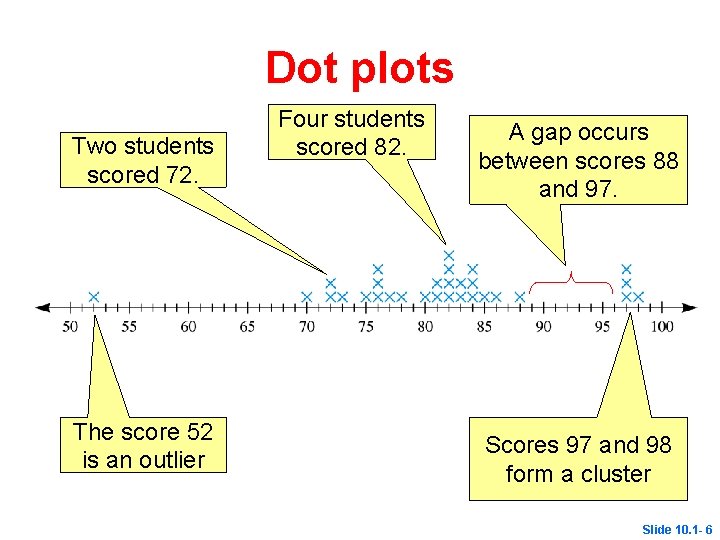
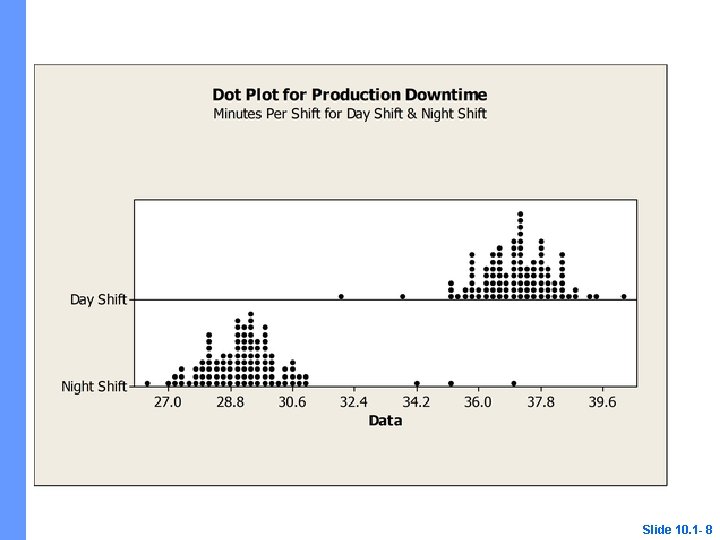
Dot Plots A dot plot for the class scores consists of a horizontal number line on which each score is denoted by a dot, or an x, above the corresponding number-line value. The number of x’s above each score indicates how many times each score occurred. Slide 10. 1 - 5

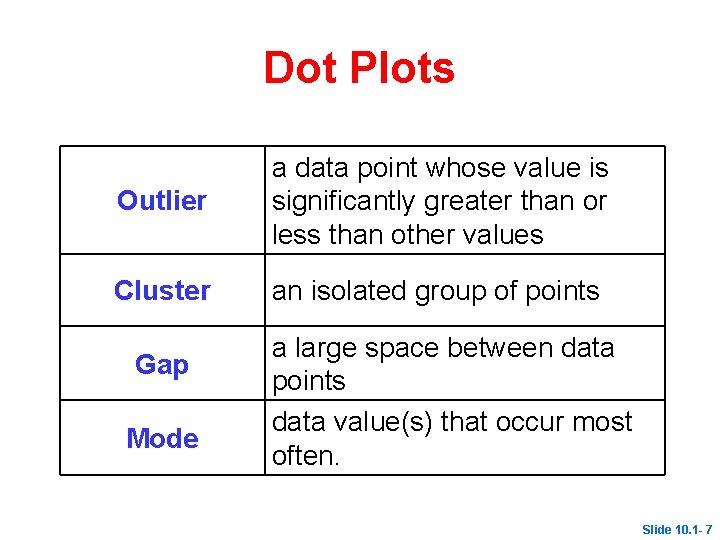
Dot plots Two students scored 72. The score 52 is an outlier Four students scored 82. A gap occurs between scores 88 and 97. Scores 97 and 98 form a cluster Slide 10. 1 - 6

Dot Plots Outlier a data point whose value is significantly greater than or less than other values Cluster an isolated group of points Gap Mode a large space between data points data value(s) that occur most often. Slide 10. 1 - 7

Slide 10. 1 - 8

Stem and Leaf Plots How to construct a stem-and-leaf plot: 1. Find the high and low values of the data. 2. Decide on the stems. 3. List the stems in a column from least to greatest. 4. Use each piece of data to create leaves to the right of the stems on the appropriate rows. Slide 10. 1 - 9

Stem and Leaf Plots 5. List the leaves in order from least to greatest. 6. Add a legend identifying the values represented by the stems and leaves. 7. Add a title explaining what the graph is about. Slide 10. 1 - 10

Stem and Leaf Plots The stem and leaf plot is similar to the dot plot, but the number line is usually vertical, and digits are used rather than x’s. 9 | 7 represents 97. Slide 10. 1 - 11

Slide 10. 1 - 12

Create a stem-and-leaf plot Cost of First year tuition at universities in the UNC system (in thousands of dollars) 3. 4, 5. 3, 4. 0, 4. 1, 3. 5, 2. 8, 5. 1, 3. 3, 3. 6, 4. 0, 4. 4, 4. 0. 4. 2, 4. 3, 4. 0 In your notes create a stem-and-leaf plot based on this information. Be sure to label the plot. Slide 10. 1 - 13

Frequency Tables Slide 10. 1 - 14

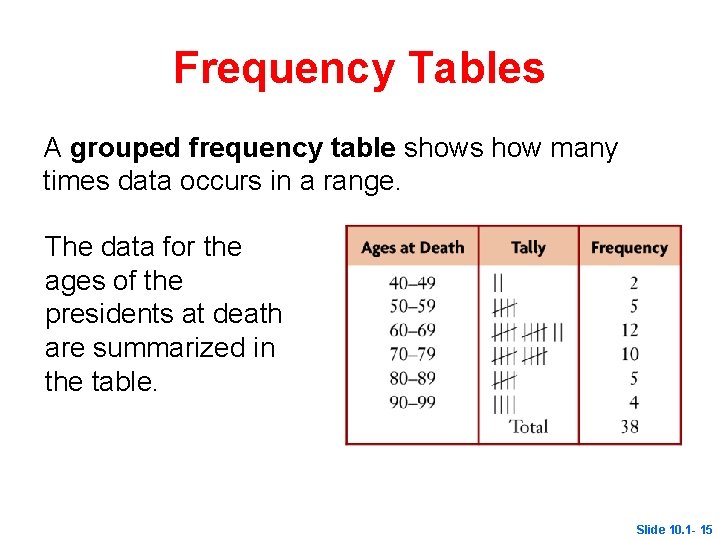
Frequency Tables A grouped frequency table shows how many times data occurs in a range. The data for the ages of the presidents at death are summarized in the table. Slide 10. 1 - 15

Frequency Tables Characteristics of Frequency Tables § Each interval has the same size. § We know how many data values occur within a particular interval but we do not know the particular data values themselves. Slide 10. 1 - 16

Frequency Tables Characteristics of Frequency Tables § As the interval size increases, information is lost. § Classes (intervals) should not overlap. Slide 10. 1 - 17

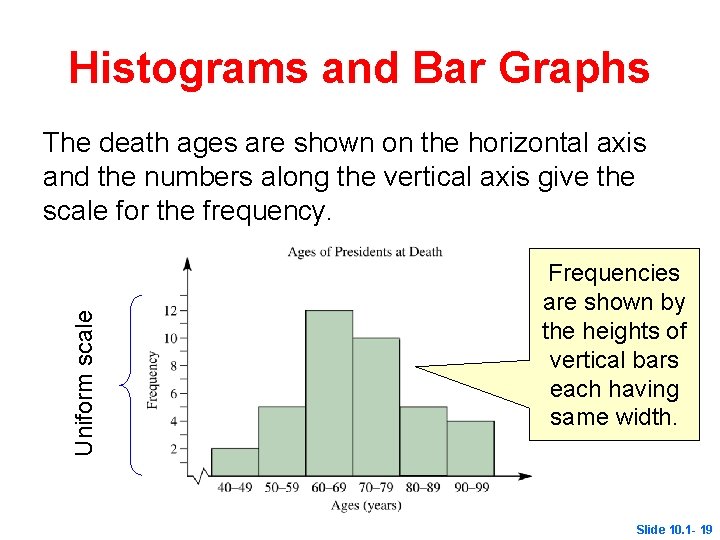
Histograms and Bar Graphs A histogram is made up of adjoining rectangles, or bars. The bars are all the same width. The scale on the vertical axis must be uniform. Slide 10. 1 - 18

Histograms and Bar Graphs Uniform scale The death ages are shown on the horizontal axis and the numbers along the vertical axis give the scale for the frequency. Frequencies are shown by the heights of vertical bars each having same width. Slide 10. 1 - 19

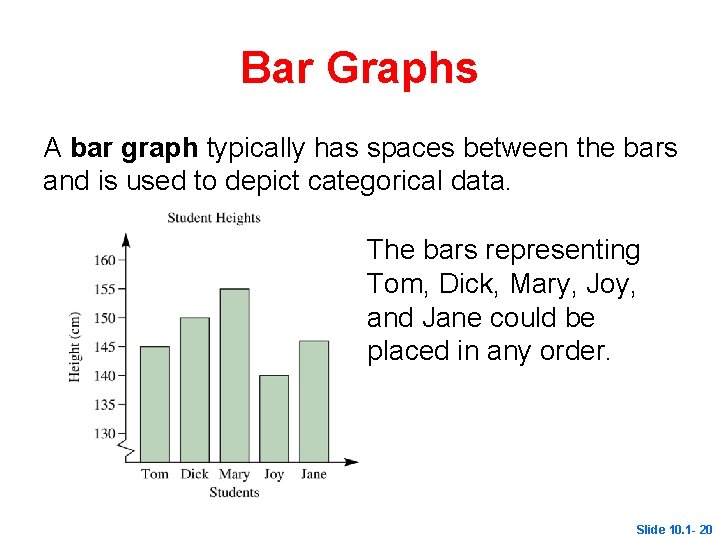
Bar Graphs A bar graph typically has spaces between the bars and is used to depict categorical data. The bars representing Tom, Dick, Mary, Joy, and Jane could be placed in any order. Slide 10. 1 - 20

Histograms and Bar Graphs A distinguishing feature between histograms and bar graphs is that there is no ordering that has to be done among the bars of the bar graph, whereas there is an order for a histogram. Slide 10. 1 - 21

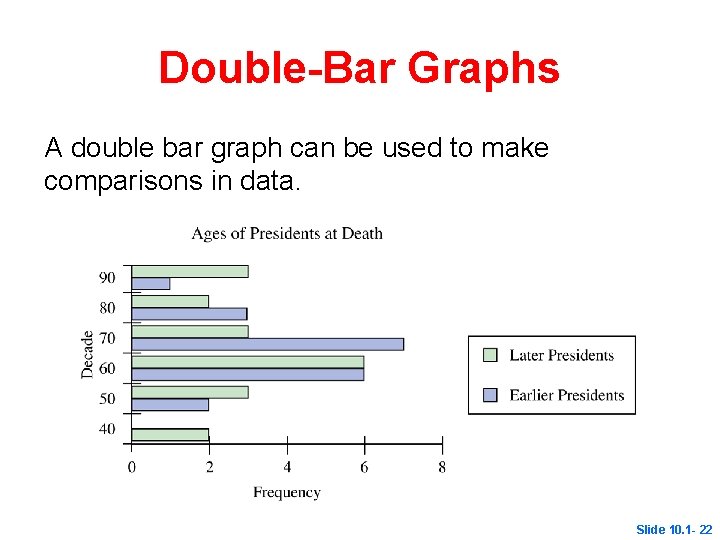
Double-Bar Graphs A double bar graph can be used to make comparisons in data. Slide 10. 1 - 22
 Stem leaf plot calculator
Stem leaf plot calculator Stem and leaf plot median
Stem and leaf plot median Id root
Id root What is the median of the data shown in the dot plot below
What is the median of the data shown in the dot plot below Double sided stem and leaf plot
Double sided stem and leaf plot Maple leaf and oak leaf homologous
Maple leaf and oak leaf homologous Leaf and non leaf procedure
Leaf and non leaf procedure Data preparing exploring examining and displaying
Data preparing exploring examining and displaying Collecting and displaying data
Collecting and displaying data Chapter 3 exploring quantitative data answers
Chapter 3 exploring quantitative data answers Categorical data displays
Categorical data displays Organizing and displaying data
Organizing and displaying data Organizing and displaying data
Organizing and displaying data Dr frost frequency tables
Dr frost frequency tables Pictograph advantages and disadvantages
Pictograph advantages and disadvantages Whats a stem and leaf plot
Whats a stem and leaf plot Stem and leaf plot
Stem and leaf plot Stem and leaf plot quiz
Stem and leaf plot quiz Graphical display of data using bars of different heights
Graphical display of data using bars of different heights Split stem and leaf plot
Split stem and leaf plot Unordered stem and leaf plot
Unordered stem and leaf plot Diagramme a tige et a feuille
Diagramme a tige et a feuille Box and whisker plot advantages
Box and whisker plot advantages