Graphs Bar Graphs A graphical display of data

Graphs

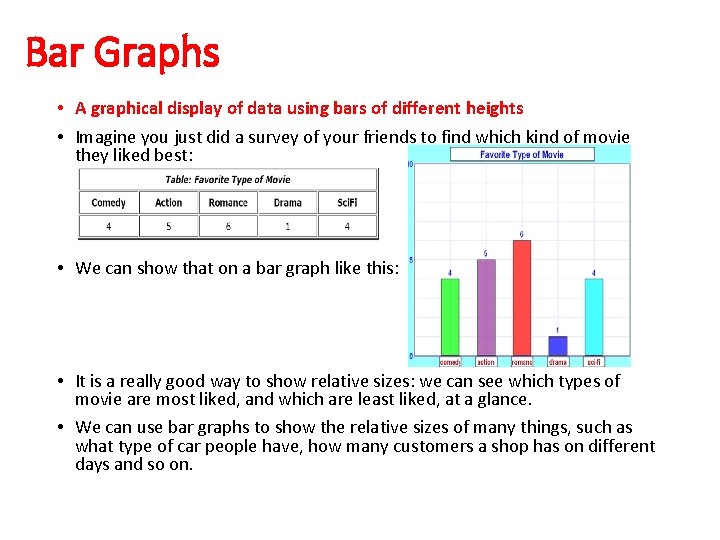
Bar Graphs • A graphical display of data using bars of different heights • Imagine you just did a survey of your friends to find which kind of movie they liked best: • We can show that on a bar graph like this: • It is a really good way to show relative sizes: we can see which types of movie are most liked, and which are least liked, at a glance. • We can use bar graphs to show the relative sizes of many things, such as what type of car people have, how many customers a shop has on different days and so on.

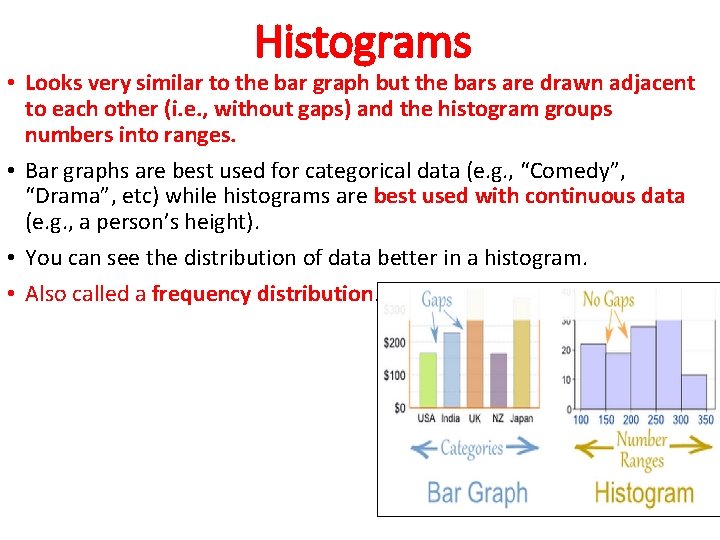
Histograms • Looks very similar to the bar graph but the bars are drawn adjacent to each other (i. e. , without gaps) and the histogram groups numbers into ranges. • Bar graphs are best used for categorical data (e. g. , “Comedy”, “Drama”, etc) while histograms are best used with continuous data (e. g. , a person’s height). • You can see the distribution of data better in a histogram. • Also called a frequency distribution.

Stem and Leaf Plot • A Stem and Leaf Plot is a special table where each data value is split into a "stem" (the first digit or digits) and a "leaf" (usually the last digit). • Ex: The "stem" values are listed down, and the "leaf" values go right (or left) from the stem values. The "stem" is used to group the scores and each "leaf" shows the individual scores within each group.

Ex: • The height of apple trees in the park are: 1. 2, 1. 3, 1. 5, 1. 7, 1. 8, 2. 2, 2. 6, 3. 5, 4. 0. Create a stem and leaf plot to display the data. Note: Stem "1" Leaf "2" means 1. 2 It is OK to repeat a leaf value. Leaves are typically arranged in increasing order. If we turn the plot on its side, we can see the distribution of data.

Stem and Leaf Discussion

Box-and-Whisker Plot • Statistics assumes that your data points (the numbers in your list) are clustered around some central value. The "box" in the boxand-whisker plot contains, and thereby highlights, the middle half of these data points. • Steps: • Order your data in numerical order • Find the median of your data (divides the data into two halves) • If you have an even number of data, average the 2 middle values • Find the median of those two halves (the Upper Quartile and Lower Quartile) • Don’t re-use the median value • Find the maximum and minimum value • Draw the box-and-whisker plot Note: The median, upper quartile and lower quartiles divide the entire data set into quarters, called "quartiles". The lower quartile is called Q 1, Q 2 is the median, and the upper quartile is called Q 3.

Ex: Draw a box-and-whisker plot for the following data set: 4. 3, 5. 1, 3. 9, 4. 5, 4. 4, 4. 9, 5. 0, 4. 7, 4. 1, 4. 6, 4. 4, 4. 3, 4. 8, 4. 4, 4. 2, 4. 5, 4. 4 • Continued…

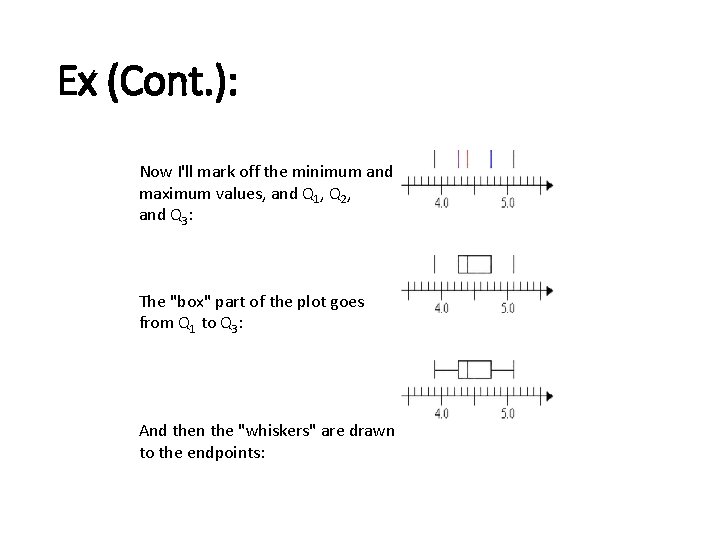
Ex (Cont. ): Now I'll mark off the minimum and maximum values, and Q 1, Q 2, and Q 3: The "box" part of the plot goes from Q 1 to Q 3: And then the "whiskers" are drawn to the endpoints:

Ex: Draw the box-and-whisker plot for the following data set: 77, 79, 80, 86, 87, 94, 99 •

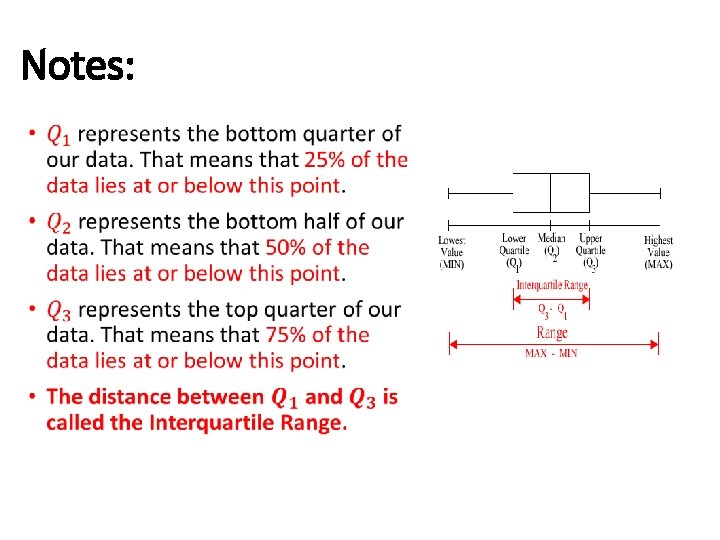
Notes: •

Box-and-Whisker Discussion