Diskreetti matematiikka 3 Lukujonoista summista ja sarjoista Langattomien

Diskreetti matematiikka 3. Lukujonoista, summista ja sarjoista Langattomien laitteiden matematiikka 1

3. 1 Lukujonon määrittely n Lukujonolla tarkoitetaan sellaista jonoa, joka saadaan kirjoittamalla lukuja peräkkäin jonkin säännön mukaan. n Esimerkki 1. Luonnolliset luvut (N) 1, 2, 3, . . . Langattomien laitteiden matematiikka 1 2

n Määritelmä 1. Lukujonolla tarkoitetaan luonnollisten lukujen joukossa määriteltyä funktiota f : N R. n Lukujonoa merkitään usein (an) tai a [n]. Langattomien laitteiden matematiikka 1 3

n n Tällöin lukujonon jäseniä merkitään nyt yleisemmässä muodossa alaindeksillä varustettuna: a 1 , a 2 , . . . , an - 1, an … Merkintää a[k] käytetään usein diskreettien systeemien ominaisuuksista puhuttaessa. Indeksi ilmaisee järjestysnumeron. Lukujonon jäsenet ovat termejä. Langattomien laitteiden matematiikka 1 4

n n Esimerkki 2. a) 1, 3, 5, 7, . . . b) 1, 4, 9, 16, 25, . . . c) 1, 2, 4, 8, 16 Lukujono voi olla päättymätön tai sitten se on päättyvä. Langattomien laitteiden matematiikka 1 5

n n Esimerkki 3. Olkoon an = 3 n + 1. Määritä lukujonon 2. ja 10. termi. Esimerkki 4. Onko luku 17 jokin jäsen jonossa(bn), kun Langattomien laitteiden matematiikka 1 6

3. 2 Aritmeettinen lukujono n Aritmeettisessa lukujonossa kaikkien jonon peräkkäisten termien erotus on vakio. Siis a 2 – a 1 = a 3 - a 2 =. . . = an - 1 = d = vakio Langattomien laitteiden matematiikka 1 7

n Tätä erotuslukua merkitään yleensä kirjaimella d. n Esimerkki 5. Mitkä esimerkin 2 lukujonoista ovat aritmeettisia? Langattomien laitteiden matematiikka 1 8

n Aritmeettisen jonon yleinen eli n: s termi voidaan esittää muodossa an = a 1 + (n – 1)d n Esimerkki 6. Osoita, että lukujono(bn), missä bn = 7 n + 2, on aritmeettinen. Langattomien laitteiden matematiikka 1 9

3. 3 Geometrinen lukujono n Geometrisessa lukujonossa kaikkien peräkkäisten termien suhde on vakio (q on suhdeluku). Siis Langattomien laitteiden matematiikka 1 10

n n Esimerkki 7. Mitkä esimerkin 2 lukujonoista ovat geometrisia? Geometrisen lukujonon yleinen termi voidaan esittää muodossa Langattomien laitteiden matematiikka 1 11

n Esimerkki 8. Osoita, että jono (cn) on geometrinen, kun Langattomien laitteiden matematiikka 1 12

3. 4 Eräitä huomautuksia n Lukujonon ei tarvitse olla aritmeettinen eikä geometrinen. n Kaikkia lukujonoja ei voida esittää säännön avulla (esimerkiksi luvun desimaaleista muodostuva lukujono). Langattomien laitteiden matematiikka 1 13

3. 5 Esimerkkejä n Esimerkki 9. Määritä geometrisen lukujonon b(n) viides termi, kun ensimmäinen termi on 4 ja suhdeluku q on 2. Langattomien laitteiden matematiikka 1 14

n Esimerkki 10. Esitä jono 10, 4, -2, … muodossa a(n) = f(n). Määritä jonon 13. jäsen n Esimerkki 11. Moniko aritmeettisen jonon 12, 19, 26, … jäsenistä on pienempi kuin 1000? Langattomien laitteiden matematiikka 1 15

n Esimerkki 12. Kuinka moni jonon 12, 0, 982 12, … jäsenistä on suurempi kuin 3? n Esimerkki 13. Onko jono a(n) = 2 5 n aritmeettinen vai geometrinen? Langattomien laitteiden matematiikka 1 16

3. 6 Lukujonon raja-arvo n Määritelmä. Lukujonolla (an) on raja-arvo a, mikäli jonon termit saadaan mielivaltaisen lähelle lukua a kunhan vain n on tarpeeksi suuri. Tällöin merkitään Langattomien laitteiden matematiikka 1 17

Langattomien laitteiden matematiikka 1 18

n Voidaan käyttää myös merkintää an a, kun n . n Tällöin sanotaan, että lukujono (an) suppenee. Muutoin sanotaan, että lukujono hajaantuu. Langattomien laitteiden matematiikka 1 19

Langattomien laitteiden matematiikka 1 20

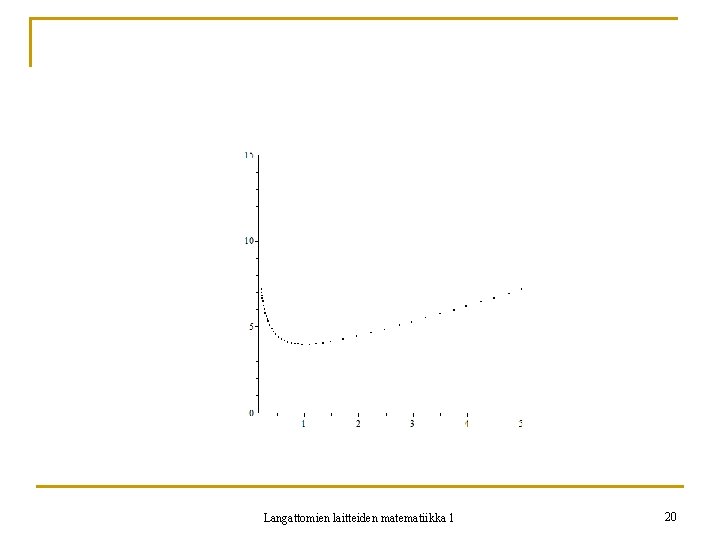
n Esimerkki 14. Mistä luvun n arvosta lähtien jonon (bn) jäsenet eroavat raja-arvosta vähemmän kuin 0, 01, kun Langattomien laitteiden matematiikka 1 21

3. 7 Geometrisen jonon suppeneminen n Geometrinen jono qn suppenee, kun -1 < q 1. n Sen avulla pystytään päättelemään monen jonon suppeneminen. Langattomien laitteiden matematiikka 1 22

3. 8 Kohti digitalisointia n n n Kun jatkuva-aikaisesta signaalista otetaan näyte, saadaan tuloksena lukujono. Tämä lukujono pyrkii kuvaamaan alkuperäistä tilannetta riittävän hyvin. Jatkuva-aikainen systeemi muuttuu siis diskreetiksi systeemiksi. Esimerkki 15. Havainnollista jonoa x[k] = k, kun k ≥ 0 sekä diskreettiä yksikköaskelfunktiota u[k]. Langattomien laitteiden matematiikka 1 23

n Esimerkki 16. Oletetaan, että tarkasteltavana on jatkuva signaali x(t) = cos t. Otetaan väliltä [0, 2 ] tasavälein i) 4 näytettä, ii) 8 näytettä. Kumpi kuvaa mielestäsi paremmin alkuperäistä signaalia? Langattomien laitteiden matematiikka 1 24

n n n Joskus diskreettiaikaiset systeemit ovat sellaisia, että niitä pystytään kuvaamaan differenssiyhtälöllä. Tällöin tiedetään sääntö, jonka mukaan edellisten tulosten perusteella saadaan uusi tieto laskettua. Differenssiyhtälöiden käyttö on erityisen tärkeää digitaalisen signaalinkäsittelyn kannalta. Langattomien laitteiden matematiikka 1 25

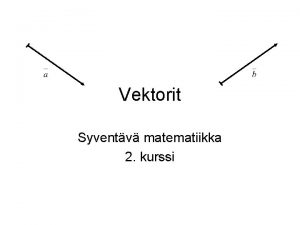
n Esimerkki 17. Tarkastellaan yksinkertaista diskreettiaikaista suodinta, jota kuvaa differenssiyhtälö y[n] – ay[n – 1] = x[n]. Yo. yhtälössä x[n] on syöte y[n] on vastejono, ja a on vakio. Määritä vastejonon 6 ensimmäistä termiä, kun syötteenä on diskreetti yksikköaskelfunktio ja a = 0, 5. Määritä lisäksi systeemin tasapainotila. Langattomien laitteiden matematiikka 1 26

3. 9 Summat n n n Matematiikassa summaa merkitään usein symbolilla (sigma). Tarkastellaan lukujonoa (an). Summamerkinnässä esiintyy melko usein indeksi, joka kertoo, mistä termistä alkaen jonon termit lasketaan yhteen. Langattomien laitteiden matematiikka 1 27

n Esimerkki 18. Merkitään summamerkinnällä lukujonon (an) 20. ensimmäisen termin summa: Langattomien laitteiden matematiikka 1 28

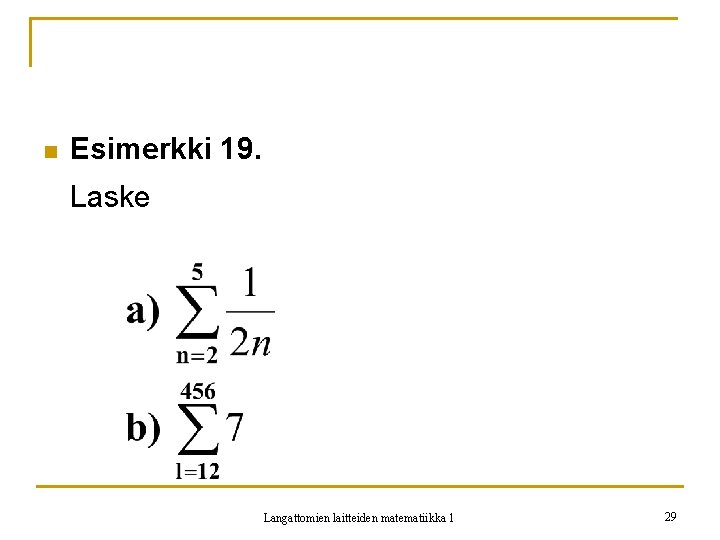
n Esimerkki 19. Laske Langattomien laitteiden matematiikka 1 29

3. 10 Aritmeettinen summa n Aritmeettisen jonon (an) n ensimmäisen jäsenen summa saadaan kaavasta Langattomien laitteiden matematiikka 1 30

n n Esimerkki 20. Laske 10000 ensimmäisen luonnollisen luvun summa. Esimerkki 21. Määritä kolminumeroisten 11 jaollisten luonnollisten lukujen summa. Langattomien laitteiden matematiikka 1 31

3. 11 Geometrinen summa n Geometrisen jonon n. ensimmäisen termin a, aq 2, …, aq n - 1 summa saadaan laskettua kaavalla (q 1) Langattomien laitteiden matematiikka 1 32

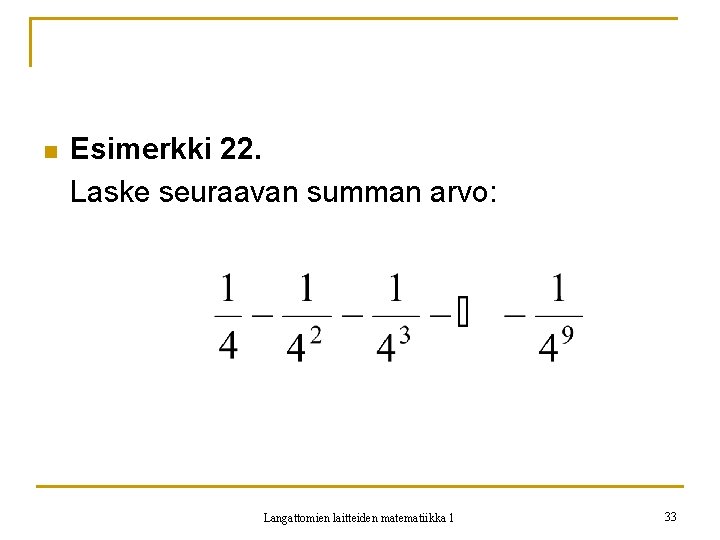
n Esimerkki 22. Laske seuraavan summan arvo: Langattomien laitteiden matematiikka 1 33

n Esimerkki 23. Kuinka monta jonon 1, 0, 992, … jäsentä on vähintään laskettava yhteen, jotta summa ylittää luvun 99? Langattomien laitteiden matematiikka 1 34

n Esimerkki 24. Tilille, jonka korko oli 4, 0 % talletettiin 20 vuoden ajan joka vuoden alussa 1000 e. Kuinka paljon rahaa tilillä oli 20. vuoden alussa? Kuinka paljon 20. vuoden lopussa? Langattomien laitteiden matematiikka 1 35

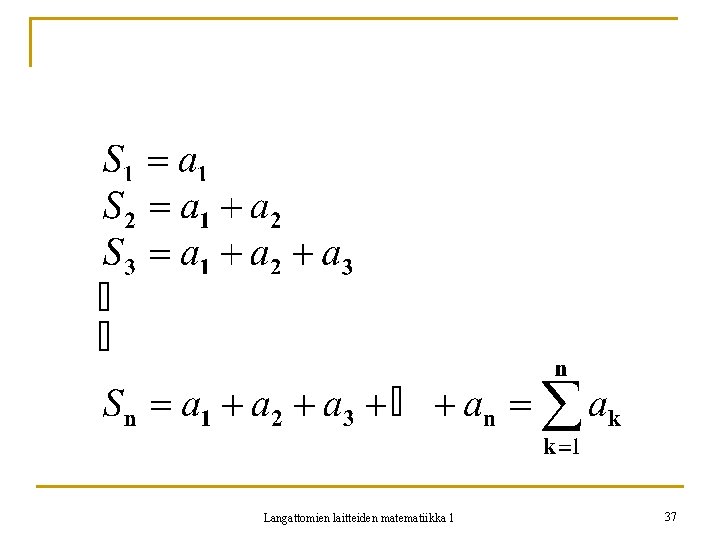
3. 12 Sarjan määrittely n Olkoon (an) päättymätön lukujono. n Muodostetaan uusi lukujono (Sn) laskemalla lukujonon (an) jäseniä yhteen. n Lukujono (Sn) on tällöin muotoa: Langattomien laitteiden matematiikka 1 36

Langattomien laitteiden matematiikka 1 37

n Lukuparia ((an), (Sn)) sanotaan sarjaksi. n Sn on sarjan n: s osasumma ja an on n: s termi tai jäsen. Sarjan merkintä: Langattomien laitteiden matematiikka 1 38

n Sarja (S) on suppeneva ja luku S on sarjan summa, jos osasummien jono (Sn) suppenee ja osasummien jonon raja-arvo n: n kasvaessa rajatta on S. Tällöin merkitään Langattomien laitteiden matematiikka 1 39

n n Jos sarja ei suppene, se hajaantuu. Esimerkki 25. Tutki, suppeneeko sarja (S 1). Määritä, mikäli mahdollista sarjan summa. Langattomien laitteiden matematiikka 1 40

n Esimerkki 26. Tutki sarjan (S 2) suppenemista ja etsi sarjan n. osasumman lauseke ja laske summan arvo, kun Langattomien laitteiden matematiikka 1 41

n n Seuraavan tuloksen avulla voidaan osoittaa, että sarja hajaantuu, mutta koskaan se ei todista, että sarja suppenisi. Lause 1. Jos sarja an suppenee, niin Langattomien laitteiden matematiikka 1 42

3. 13 Geometrinen sarja n Tarkastellaan geometrista sarjaa (G), joka saadaan laskemalla yhteen geometrisen jonon peräkkäisiä termejä: Langattomien laitteiden matematiikka 1 43

n Lause 2. Geometrinen sarja (G) suppenee, kun geometrisen jonon suhdeluku x toteuttaa ehdon | x | < 1. Tällöin sarjan summa on Langattomien laitteiden matematiikka 1 44

n Esimerkki 27. Esitä desimaaliluku 0, 5454… murtolukuna. n Esimerkki 28. Laske summa Langattomien laitteiden matematiikka 1 45

n Esimerkki 29. Milloin sarja (S 1) suppenee ja mikä on sen summa? Langattomien laitteiden matematiikka 1 46

n Esimerkki 30. Millä muuttujan arvoilla sarja suppenee. Mikä on sarjan summa? Langattomien laitteiden matematiikka 1 47

3. 14 Yleistä sarjaoppia n n n Seuraavassa tarkastellaan positiivitermisiä sarjoja. Sarja on positiiviterminen, jos an > 0 kaikilla n N. Tarkastellaan ensin suppenemista yleisesti ja sen jälkeen esitetään keinoja suppenevuustarkasteluihin. Langattomien laitteiden matematiikka 1 48

n Lause 3. Jos sarjat an ja bn suppenevat ja niiden summat ovat A ja B, niin sarjat kan, kbn ja (an + bn) suppenevat ja niiden summat ovat k. A, k. B, ja A + B. Langattomien laitteiden matematiikka 1 49

n n Lause 3 sanoo sen, että ainoastaan suppenevat sarjat voidaan laskea yhteen ja kertoa vakiolla. Seuraavassa monisteessa on luettelonomaisesti kerrottu, mitä ”testiä” suppenemisen tarkastelemiseksi on käytettävä. Langattomien laitteiden matematiikka 1 50

n Esimerkkejä löytyy kirjallisuudesta, vaikkakin tämän mielenkiintoisen aiheen joudumme sivuuttamaan. Langattomien laitteiden matematiikka 1 51

3. 15 Potenssisarjat n n Sovellusten kannalta tärkeitä sarjoja ovat potenssisarjat. Potenssisarjojen yleinen muoto on Langattomien laitteiden matematiikka 1 52

n Usein riittää tarkastella muotoa (P 2) olevia potenssisarjoja. Langattomien laitteiden matematiikka 1 53

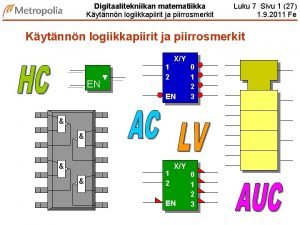
n n Sarjan (P 2) suppenemisalue on origokeskinen väli ] –R, R[, kun taas yleisem-män potenssisarjan suppenemisväli on yleensä ]x 0 – R, x 0 + R[. Yleinen tarkastelu sivuutetaan. Langattomien laitteiden matematiikka 1 54

n Todetaan lyhyesti: - jos suppenemissäde on , niin sarja suppenee reaalilukujen joukossa - jos suppenemissäde on 0, niin sarja suppenee vain yhdessä pisteessä x 0 Langattomien laitteiden matematiikka 1 55

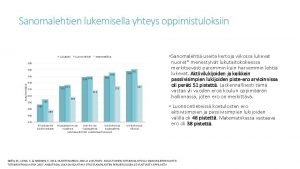
n Sarjaa (P) voidaan derivoida termeittäin välin ]-R, R[ jokaisessa pisteessä ja Langattomien laitteiden matematiikka 1 56

n Seuraavassa tutustutaan Taylorin ja Mc. Laurinin sarjakehitelmiin. Langattomien laitteiden matematiikka 1 57

3. 16 Taylorin sarja ja polynomi n n Potenssisarja esittää suppenemisalueessaan funktiota. Käsitellään käänteistä tilannetta, ja tutkitaan, onko mahdollista liittää annettuun funktioon potenssisarja, joka esittää tätä funktiota. Langattomien laitteiden matematiikka 1 58

n Lause 4. Jos funktio f ja sen n + 1 ensimmäistä derivaattaa ovat jatkuvia välillä [a, b], niin kaikilla x 0 [a, b] on funktiolle f olemassa esitys Langattomien laitteiden matematiikka 1 59

Langattomien laitteiden matematiikka 1 60

missä jäännöstermi Rn+1 on Langattomien laitteiden matematiikka 1 61

n Mikäli funktio f voidaan derivoida äärettömän monta kertaa suppenemisvälillä ja jäännöstermi Rn+1 0, kun n , niin funktio f voidaan esittää suppenemisvälillä ]x 0 - R, x 0 + R [ potenssisarjan summan muodossa Langattomien laitteiden matematiikka 1 62

n Sarjaa (T) sanotaan Taylorin sarjaksi pisteessä x 0. Langattomien laitteiden matematiikka 1 63

n n Sarjan (T) suppenemista voidaan periaatteessa tutkia samoilla menetelmillä kuin muidenkin potenssisarjojen suppenemista. Sarjan (T) n. osasummaa sanotaan n. astetta olevaksi Taylorin polynomiksi, ja sen muoto on Langattomien laitteiden matematiikka 1 64

n Ei ole kuitenkaan itsestäänselvää, että sarjan (T) summafunktio olisi f (x). Yleisesti ottaen päättelyn vahvistaminen vaatii jäännöstermin tutkimisen. Langattomien laitteiden matematiikka 1 65

n Lause 5. (Yksikäsitteisyyslause) Jos funktiolla f on potenssisarjaesitys (P) välillä ] x 0 - R, x 0 + R[ , Langattomien laitteiden matematiikka 1 66

missä on (P) samalla ko. funktion Taylorin sarja. Langattomien laitteiden matematiikka 1 67

n Eli saatiin: Taylorin sarja: Taylorin polynomi: Langattomien laitteiden matematiikka 1 68

Eräs huomautus n Kun muodostetaan Taylorin sarja pisteessä x 0 = 0, niin saadaan Mc. Laurinin sarja. Langattomien laitteiden matematiikka 1 69

3. 17 Esimerkkejä n Esimerkki 31. Johdetaan funktion f (x) = cos x Taylorin sarja pisteessä x 0 = 0 (ns. Mc. Laurinin sarja). Miten saadaan nyt helposti johdettua sinifunktion Mc. Laurinin sarja? Langattomien laitteiden matematiikka 1 70

n Esimerkki 32. Etsitään Mc. Laurinin sarja funktiolle n Esimerkki 33. Määritä raja-arvo Langattomien laitteiden matematiikka 1 71

n Esimerkki 34. Etsi kaavastosta binomisarjan esitys ja määritä Mc. Laurinin kehitelmä funktiolle Langattomien laitteiden matematiikka 1 72

n Esimerkki 35. Ratkaise differentiaaliyhtälö Langattomien laitteiden matematiikka 1 73

3. 18 Linearisointi n n n Linearisoinnin tarkoituksena on saattaa vaikea matemaattinen funktio yksinkertaisempaan esitystapaan. Esimerkiksi neliöjuurifunktiota voidaan approksimoida 1. asteen polynomilla, sinifunktio korvata x: lla kulmamuutoksen ollessa pieni jne. Katsotaan esimerkkejä luennolla. Langattomien laitteiden matematiikka 1 74

3. 19 Lisää sovelluksia n n Katsotaan seuraavaksi sovellusta digitaaliseen maailmaan: FIR-suodatus. Esimerkki 36. Tarkastellaan äärelliskestoista signaalia x[0] = 2, x[1] = 4 ja x[2] = 6. Käytettäessä 3 pisteen reaaliaikaista keskiarvonlaskijaa saadaan vastaukseksi 4. Esitä signaali ja vaste graafisesti, kun n = -3. . 5. Langattomien laitteiden matematiikka 1 75

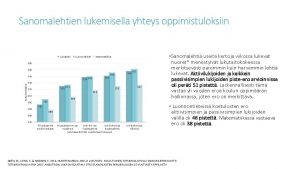
n Esimerkki 37. Oletetaan, että ohjaussignaali on muotoa x[n] = 1, 02 n + 0, 5 cos((n+1)* /4), kun 0 n 40 ja 0 muulloin. Katsotaan, miten kohinan poistaminen tapahtuu. Langattomien laitteiden matematiikka 1 76