DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF JOENSUU FINLAND

DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF JOENSUU, FINLAND Design and Analysis of Algorithms Lecture Dynamic programming Alexander Kolesnikov 17. 10. 205

List of sample problems • Shortest path in trellis graph; • Optimal allocation of constrained resource; • Optimal sequence partition (k-link shortest path). • to be continued. . .

Shortest path in trellis graph

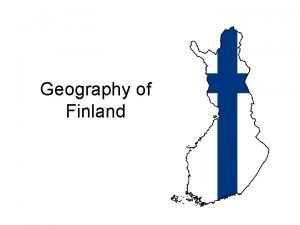
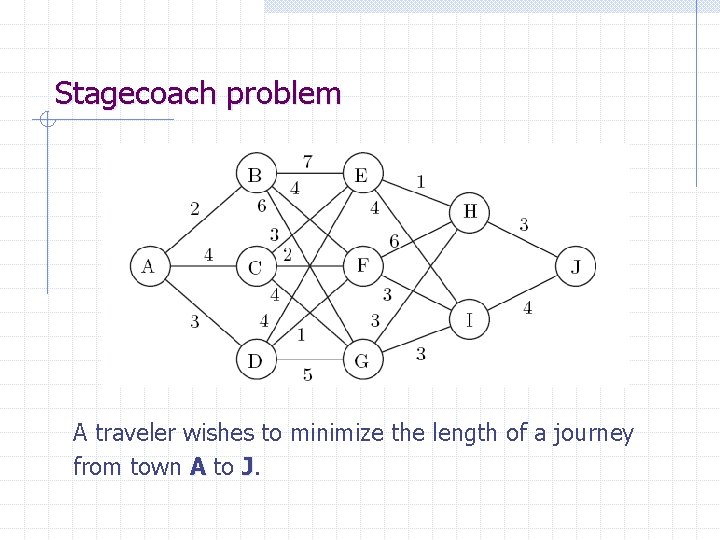
Stagecoach problem A traveler wishes to minimize the length of a journey from town A to J.

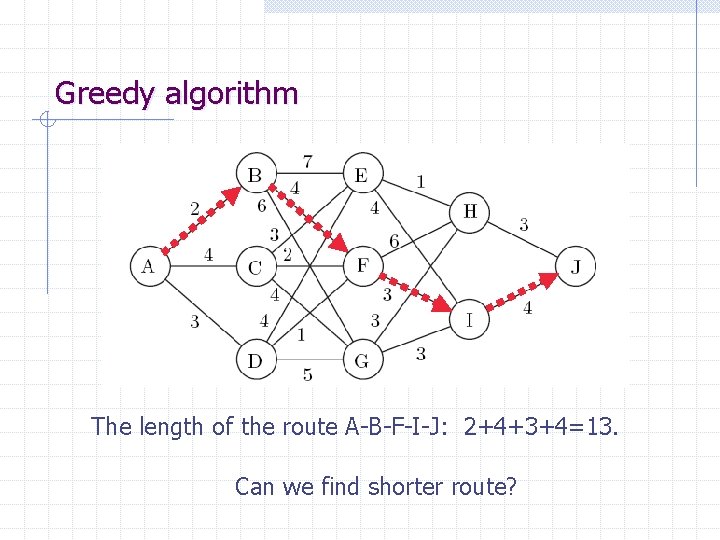
Greedy algorithm The length of the route A-B-F-I-J: 2+4+3+4=13. Can we find shorter route?

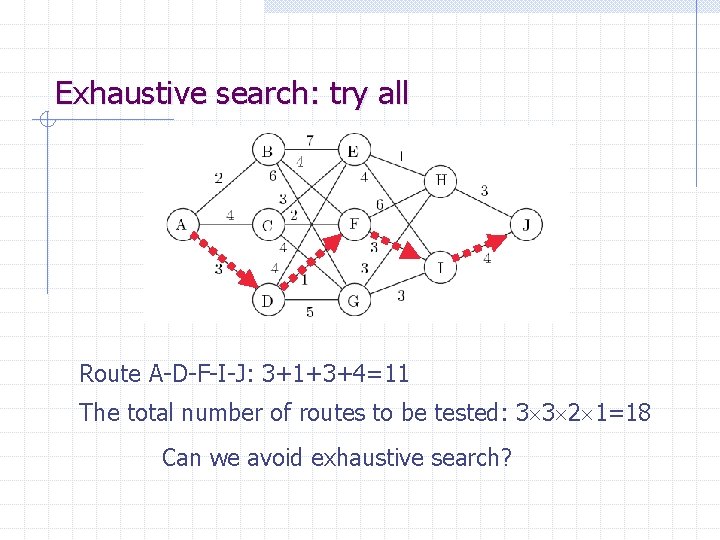
Exhaustive search: try all Route A-D-F-I-J: 3+1+3+4=11 The total number of routes to be tested: 3 3 2 1=18 Can we avoid exhaustive search?

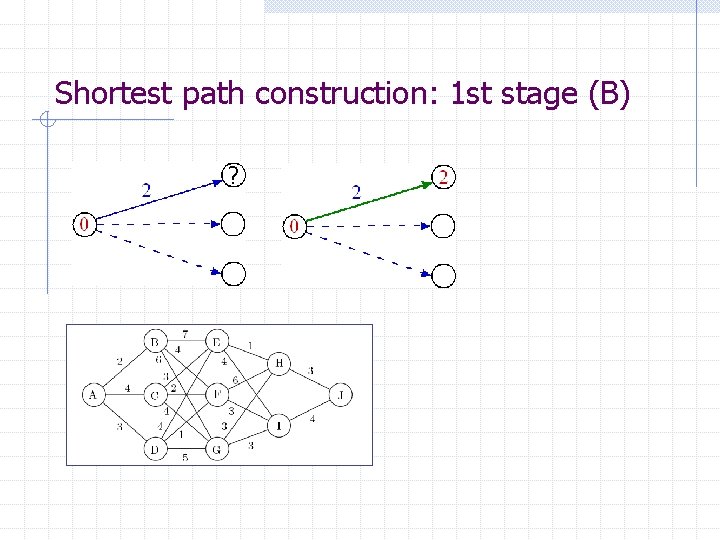
Shortest path construction: 1 st stage (B) ?

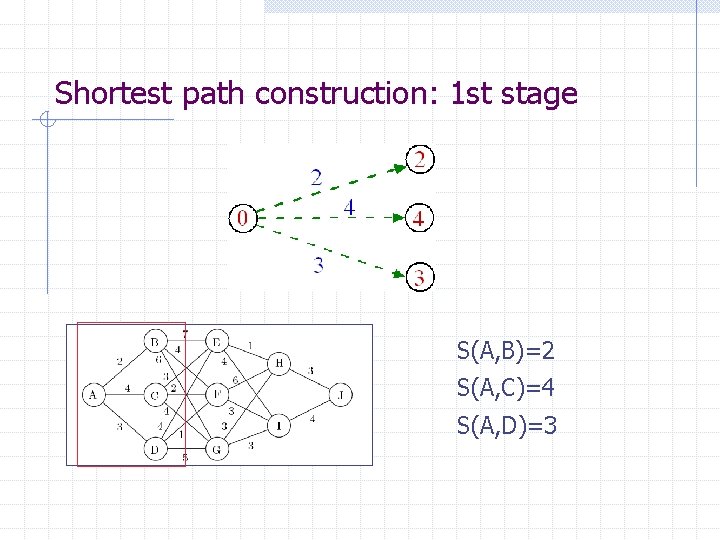
Shortest path construction: 1 st stage S(A, B)=2 S(A, C)=4 S(A, D)=3

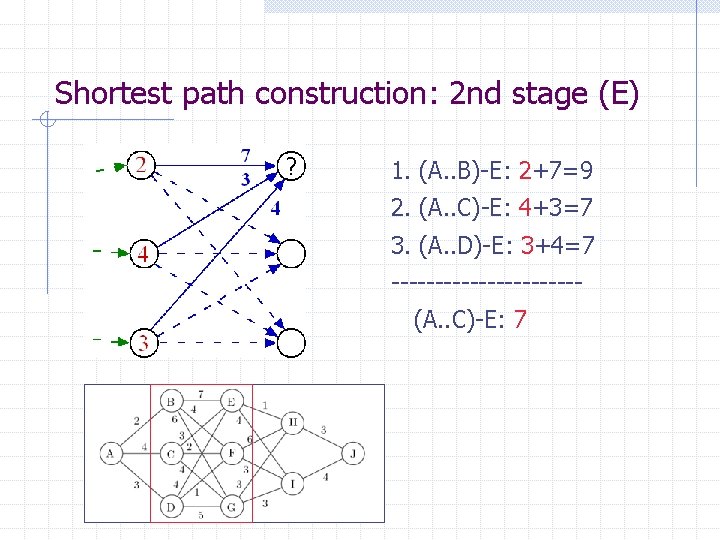
Shortest path construction: 2 nd stage (E) ? 1. (A. . B)-E: 2+7=9 2. (A. . C)-E: 4+3=7 3. (A. . D)-E: 3+4=7 -----------(A. . C)-E: 7

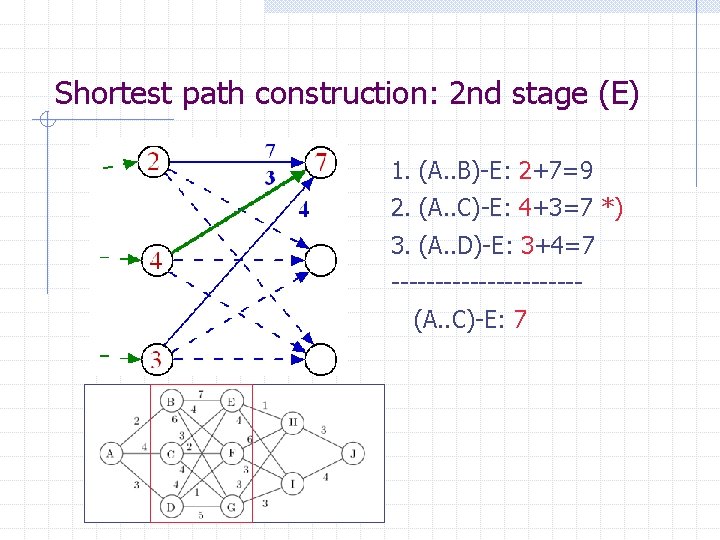
Shortest path construction: 2 nd stage (E) 1. (A. . B)-E: 2+7=9 2. (A. . C)-E: 4+3=7 *) 3. (A. . D)-E: 3+4=7 -----------(A. . C)-E: 7

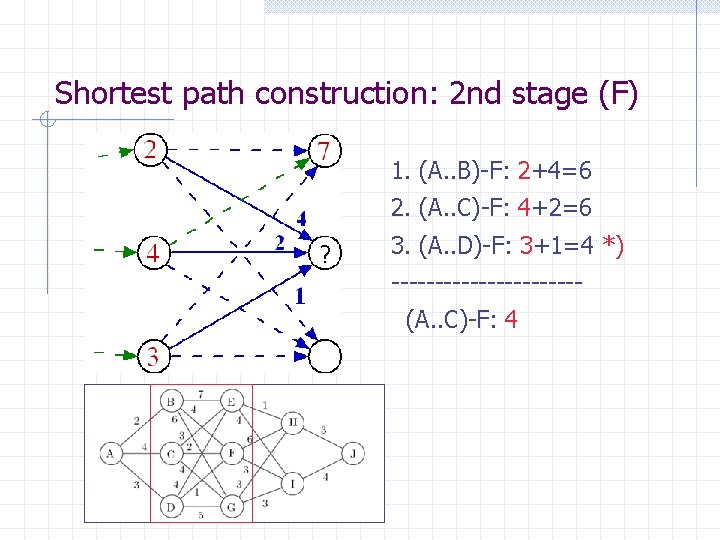
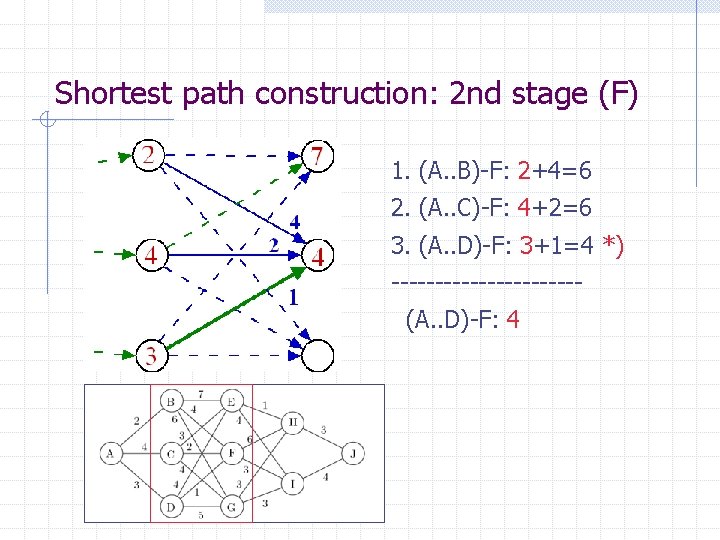
Shortest path construction: 2 nd stage (F) 1. (A. . B)-F: 2+4=6 2. (A. . C)-F: 4+2=6 ? 3. (A. . D)-F: 3+1=4 *) -----------(A. . C)-F: 4

Shortest path construction: 2 nd stage (F) 1. (A. . B)-F: 2+4=6 2. (A. . C)-F: 4+2=6 3. (A. . D)-F: 3+1=4 *) -----------(A. . D)-F: 4

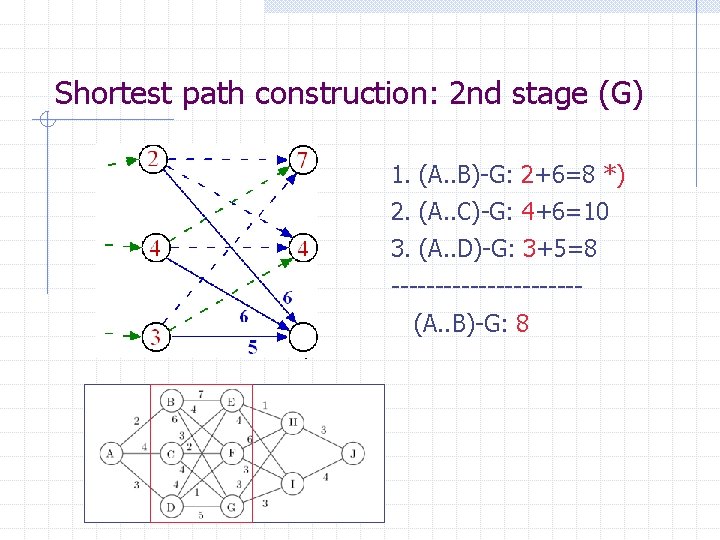
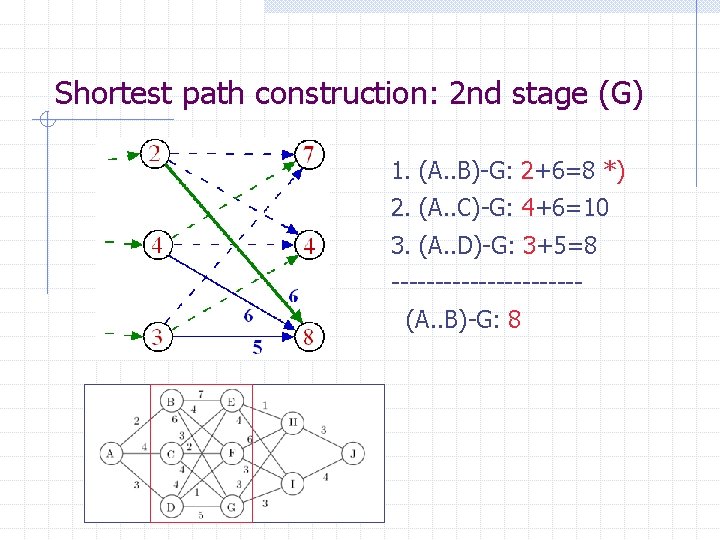
Shortest path construction: 2 nd stage (G) 1. (A. . B)-G: 2+6=8 *) 2. (A. . C)-G: 4+6=10 3. (A. . D)-G: 3+5=8 -----------? (A. . B)-G: 8

Shortest path construction: 2 nd stage (G) 1. (A. . B)-G: 2+6=8 *) 2. (A. . C)-G: 4+6=10 3. (A. . D)-G: 3+5=8 -----------(A. . B)-G: 8

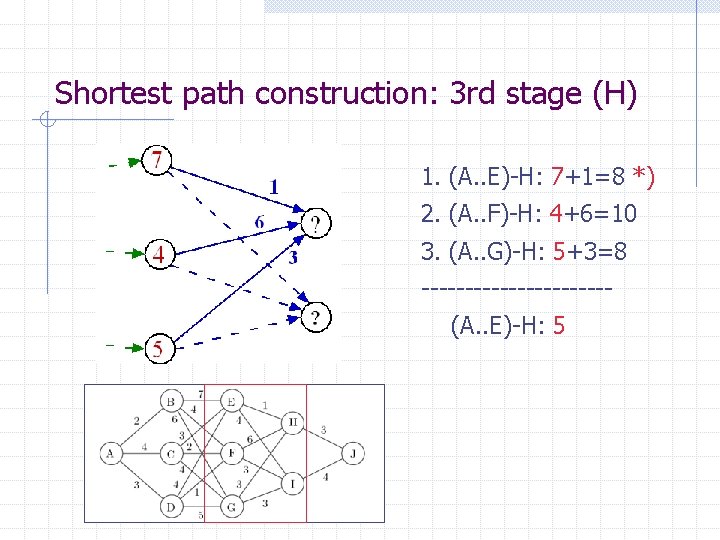
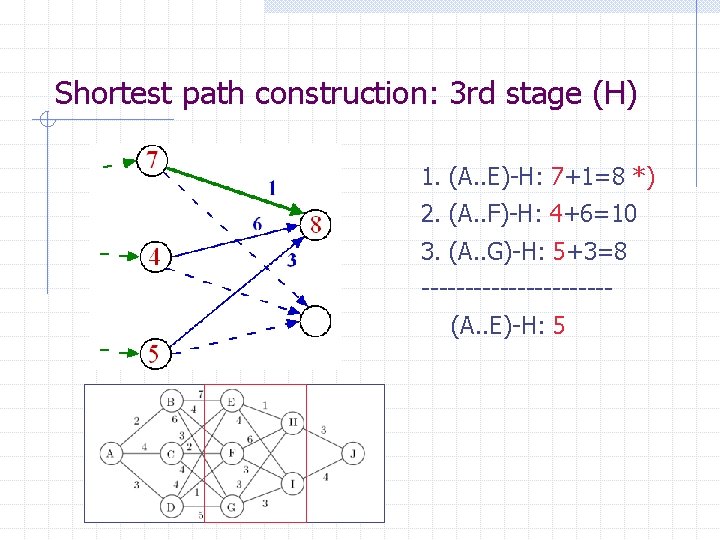
Shortest path construction: 3 rd stage (H) 1. (A. . E)-H: 7+1=8 *) 2. (A. . F)-H: 4+6=10 3. (A. . G)-H: 5+3=8 -----------(A. . E)-H: 5

Shortest path construction: 3 rd stage (H) 1. (A. . E)-H: 7+1=8 *) 2. (A. . F)-H: 4+6=10 3. (A. . G)-H: 5+3=8 -----------(A. . E)-H: 5

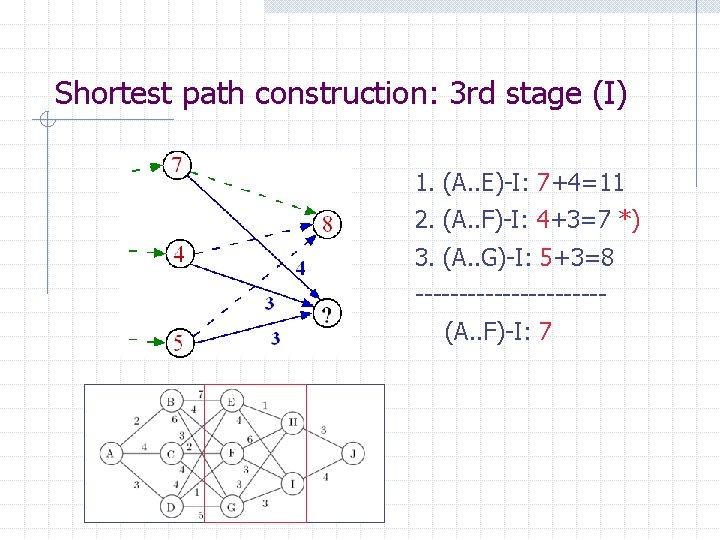
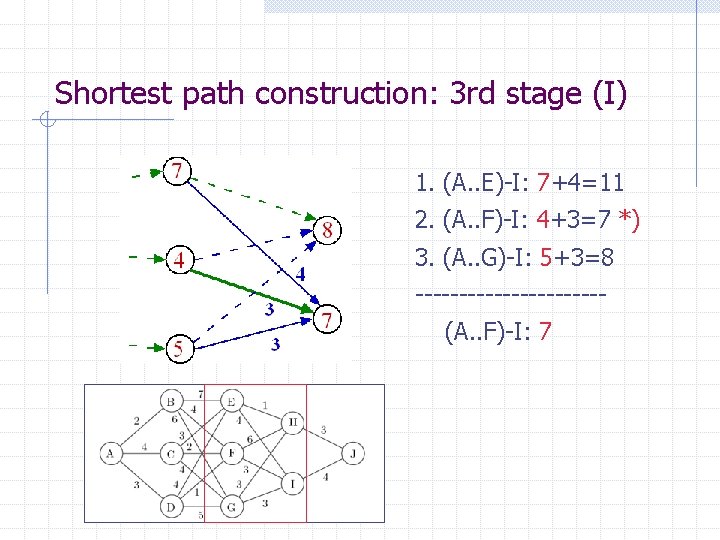
Shortest path construction: 3 rd stage (I) 1. (A. . E)-I: 7+4=11 2. (A. . F)-I: 4+3=7 *) 3. (A. . G)-I: 5+3=8 -----------(A. . F)-I: 7

Shortest path construction: 3 rd stage (I) 1. (A. . E)-I: 7+4=11 2. (A. . F)-I: 4+3=7 *) 3. (A. . G)-I: 5+3=8 -----------(A. . F)-I: 7

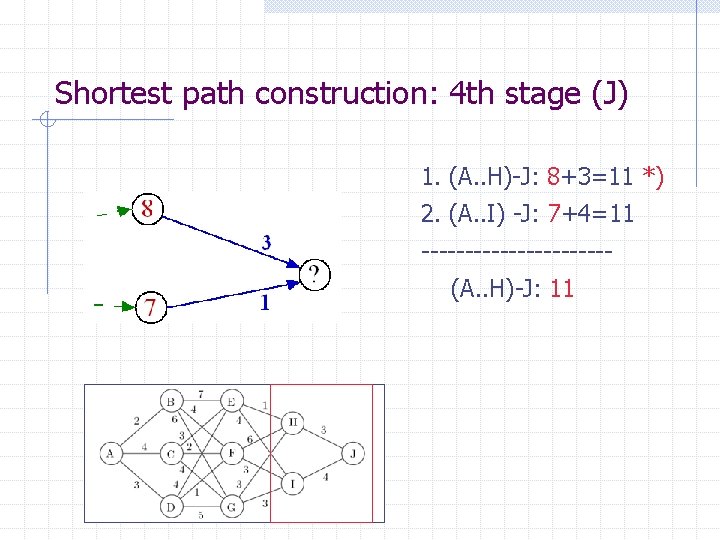
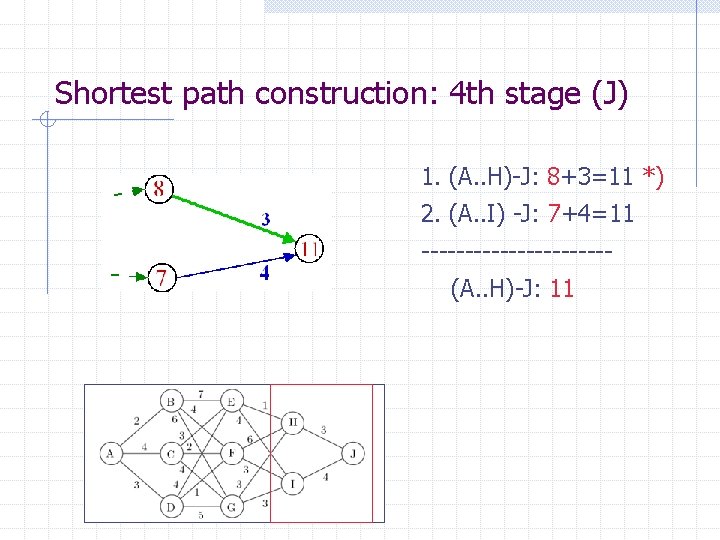
Shortest path construction: 4 th stage (J) 1. (A. . H)-J: 8+3=11 *) 2. (A. . I) -J: 7+4=11 -----------(A. . H)-J: 11

Shortest path construction: 4 th stage (J) 1. (A. . H)-J: 8+3=11 *) 2. (A. . I) -J: 7+4=11 -----------(A. . H)-J: 11

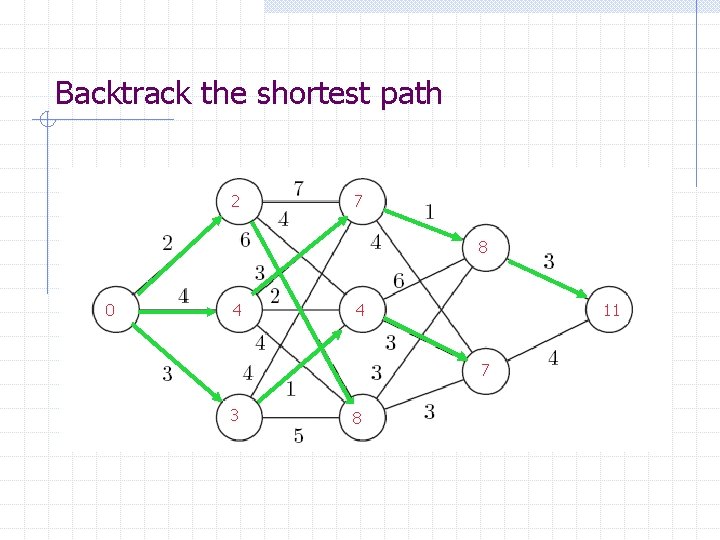
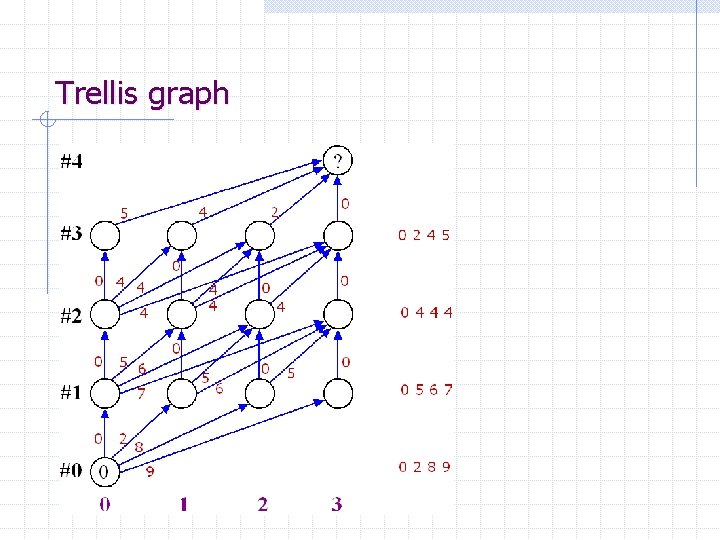
Backtrack the shortest path 2 7 8 0 4 4 11 7 3 8

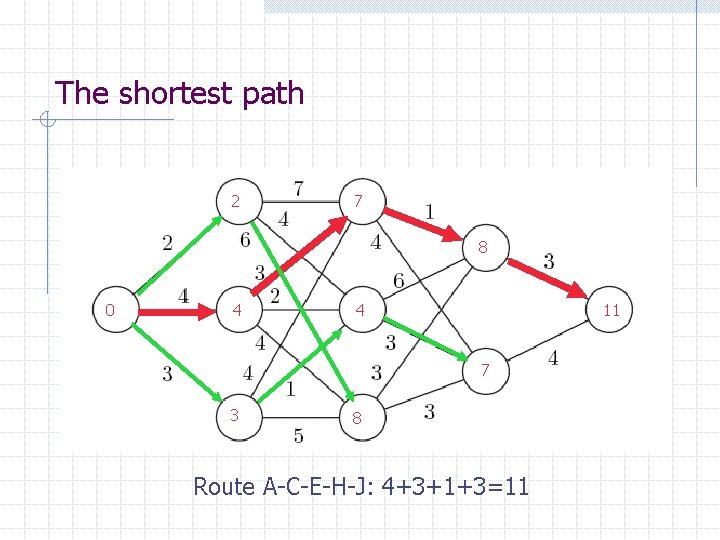
The shortest path 2 7 8 0 4 4 11 7 3 8 Route A-C-E-H-J: 4+3+1+3=11

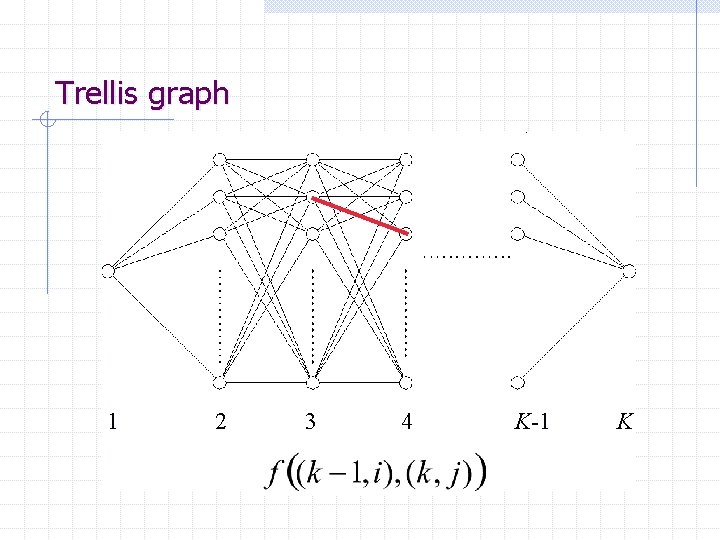
Trellis graph 1 2 3 4 K-1 K

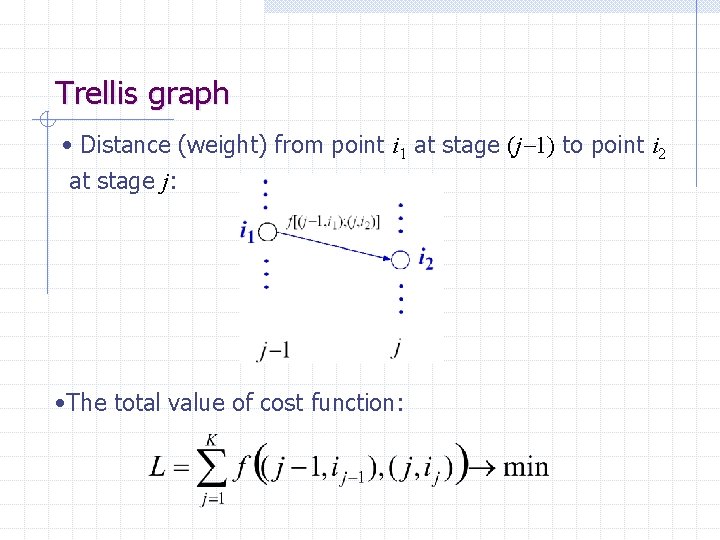
Trellis graph • Distance (weight) from point i 1 at stage (j 1) to point i 2 at stage j: • The total value of cost function:

Principle of optimality of Bellman An optimal path has the property that whatever the initial conditions and control variables (choices) over some initial period, the control (or decision variables) chosen over the remaining period must be optimal for the remaining problem, with the state resulting from the early decisions taken to be the initial condition.

Dynamic programming • Cost function: • Recursive eqution: • Initialization:

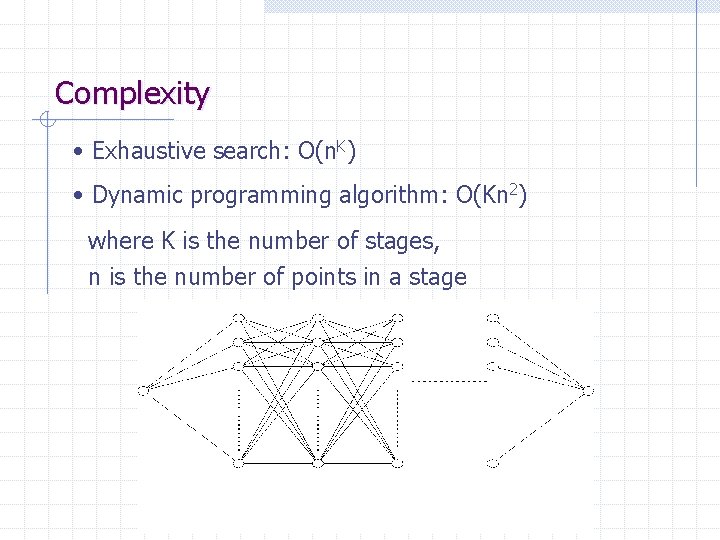
Complexity • Exhaustive search: O(n. K) • Dynamic programming algorithm: O(Kn 2) where K is the number of stages, n is the number of points in a stage

Optimal allocation of constrained resource

Problem formulation • N units of a resource; • This resource must be distributed among K activities; • Functions fk(x) - profit for allocated resource; • Allocate N units of resource to K activities with given return functions so that the total profit is maximal: subject to:

Dynamic programming formulation Optimal value function: Recursive equation: Initialization:

Allocate 3 mln euros into four projects Profit fk(x), K=3, N=3.

Trellis graph

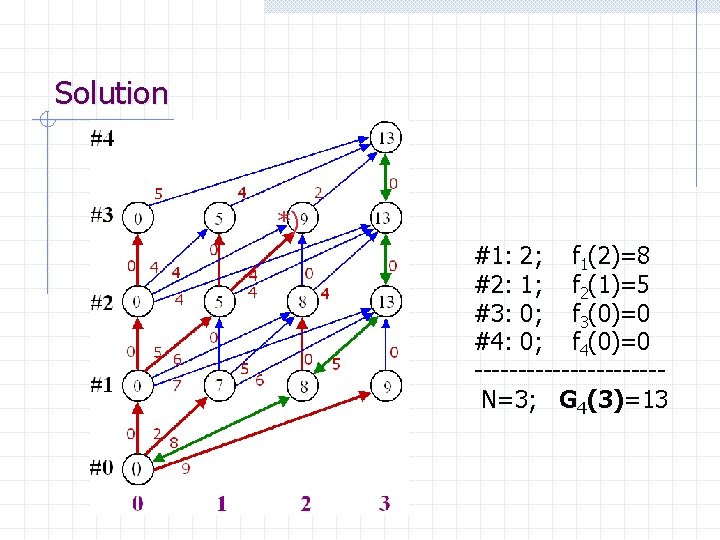
Solution *) #1: 2; f 1(2)=8 #2: 1; f 2(1)=5 #3: 0; f 3(0)=0 #4: 0; f 4(0)=0 -----------N=3; G 4(3)=13

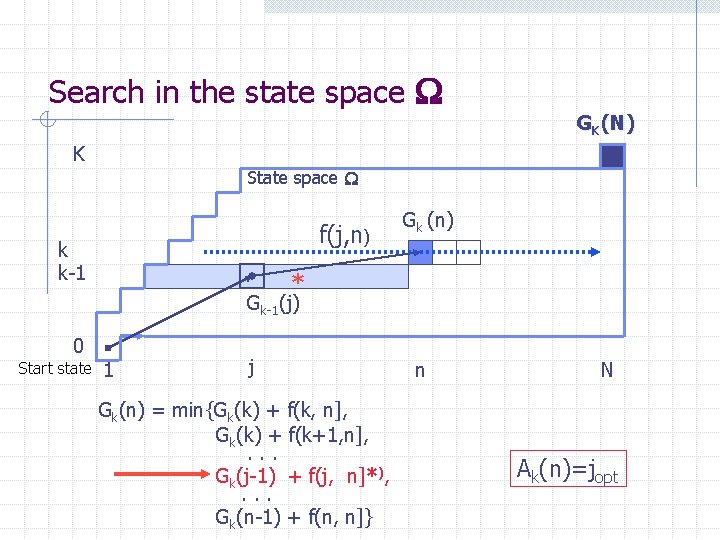
Search in the state space GK(N) K fk(n-j) k k-1 1 0 Start state Gk(n) * Gk-1(j) 0 j Gk(n) = max{Gk(0) + fk(n), Gk(1) + fk(n-1), . . . Gk(j-1)+ fk(j), . . . Gk(n) + fk(0)} n N Ak(n)=jopt

Optimal partition of data sequence

Problem formulation Given a sequence of data X={x 1, x 2, …, x. N} Do partition of the sequence X into to K groups with given cost functions f(xi, xj) so that the total value of the cost function is minimal:

Partition into groups: Example • Data: x 0= < x 1 <. . . < xj <. . . < x. N • Partition indices: i 0= 0 < i 1 <. . . < ij <. . . < i. M =N. • Groups: #1 • . . . ( • • • (x 0= ) x 1 x 2 x 3 (i 0=0) #2 • ]( • • • x 4 i 1=4 K=3 #3 x 5 x 6 x 7 x 8 x 9 • ]( • • • ] x 10 x 11 x 12 x 13 x 14 x. N i 2=10 i. K =N=15

Problem formulation Cost function: Recursive equation: Initialization:

Search in the state space K GK(N) b State space f(j, n) k k-1 Gk (n) * Gk-1(j) 0 Start state 1 j Gk(n) = min{Gk(k) + f(k, n], Gk(k) + f(k+1, n], . . . Gk(j-1) + f(j, n]*), . . . Gk(n-1) + f(n, n]} n N Ak(n)=jopt

Scheme of the DP algorithm // Initialization FOR n = 1 TO N DO G 1(n)= (n) f(1, n] // Minimum search FOR k = 2 TO K DO FOR n = k TO N DO dmin FOR j= k-1 TO n-1 DO c Gk-1(j) + f(j, n] IF(c < cmin) cmin c; jmin j ENDIF ENDFOR Gk (n) dmin Ak (n) jmin ENDFOR Complexity: O(KN 2)

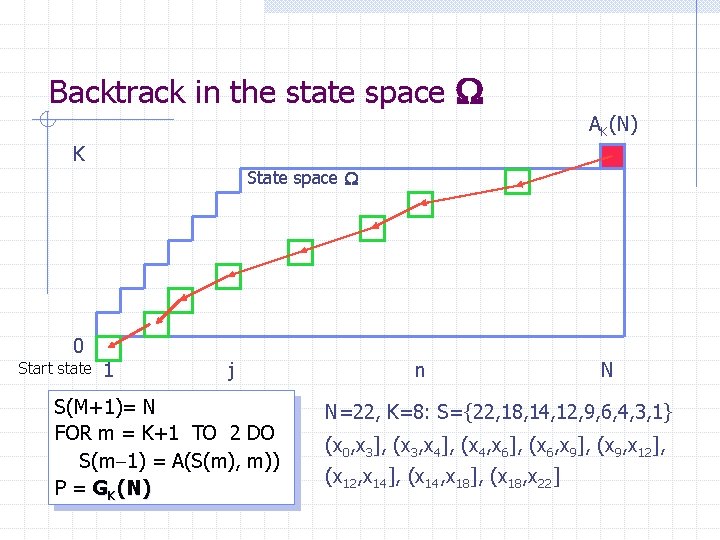
Backtrack in the state space AK(N) K b State space 0 Start state 1 j S(M+1)= N FOR m = K+1 TO 2 DO S(m 1) = A(S(m), m)) P = GK(N) n N N=22, K=8: S={22, 18, 14, 12, 9, 6, 4, 3, 1} (x 0, x 3], (x 3, x 4], (x 4, x 6], (x 6, x 9], (x 9, x 12], (x 12, x 14], (x 14, x 18], (x 18, x 22]