Data Mining Spring 2007 Noisy data Data Discretization








![Chi. Merge Example (cont. ) 2 was minimum for intervals: [7. 5, 8. 5] Chi. Merge Example (cont. ) 2 was minimum for intervals: [7. 5, 8. 5]](https://slidetodoc.com/presentation_image_h/31c2a2a2eb32b5dc60b7e797c1e636d4/image-17.jpg)
![Chi. Merge Example (cont. ) Additional Iterations: K=1 K=2 Interval [0, 7. 5] A Chi. Merge Example (cont. ) Additional Iterations: K=1 K=2 Interval [0, 7. 5] A](https://slidetodoc.com/presentation_image_h/31c2a2a2eb32b5dc60b7e797c1e636d4/image-18.jpg)


- Slides: 20

Data Mining Spring 2007 • Noisy data • Data Discretization using Entropy based and Chi. Merge

Noisy Data • Noise: Random error, Data Present but not correct. – Data Transmission error – Data Entry problem • Removing noise – Data Smoothing (rounding, averaging within a window). – Clustering/merging and Detecting outliers. • Data Smoothing – First sort the data and partition it into (equi-depth) bins. – Then the values in each bin using Smooth by Bin Means, Smooth by Bin Median, Smooth by Bin Boundaries, etc.

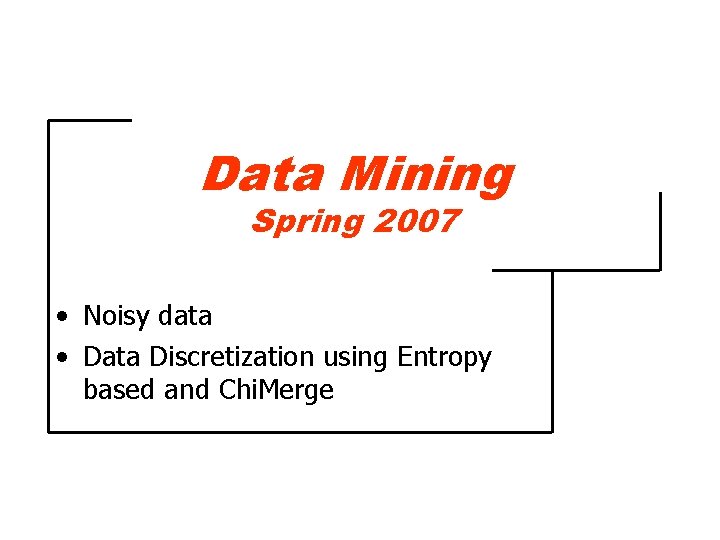
Noisy Data (Binning Methods) Sorted data for price (in dollars): 4, 8, 9, 15, 21, 24, 25, 26, 28, 29, 34 * Partition into (equi-depth) bins: - Bin 1: 4, 8, 9, 15 - Bin 2: 21, 24, 25 - Bin 3: 26, 28, 29, 34 * Smoothing by bin means: - Bin 1: 9, 9, 9, 9 - Bin 2: 23, 23, 23 - Bin 3: 29, 29, 29 * Smoothing by bin boundaries: - Bin 1: 4, 4, 4, 15 - Bin 2: 21, 25, 25 - Bin 3: 26, 26, 34

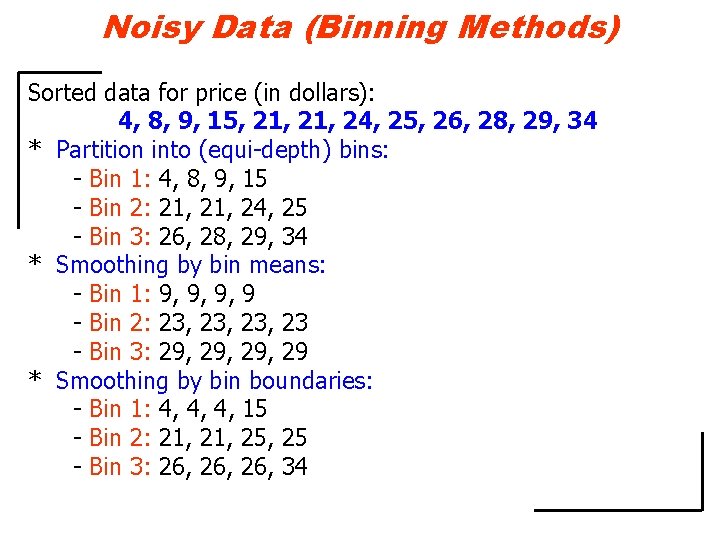
Noisy Data (Clustering) • Outliers may be detected by clustering, where similar values are organized into groups or “clusters”. • Values which falls outside of the set of clusters may be considered outliers.

Data Discretization • The task of attribute (feature)-discretization techniques is to discretize the values of continuous features into a small number of intervals, where each interval is mapped to a discrete symbol. • Advantages: - – Simplified data description and easy-to-understand data and final data-mining results. – Only Small interesting rules are mined. – End-results processing time decreased. – End-results accuracy improved.

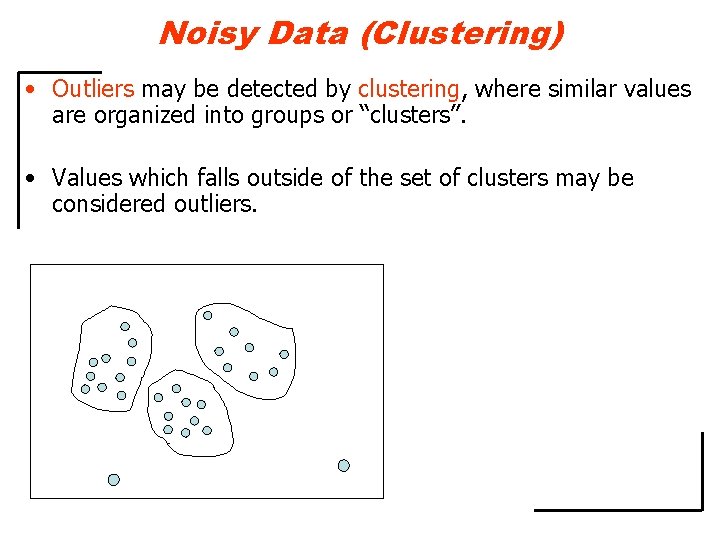
Effect of Continuous Data on Results Accuracy Data Mining • If ‘age <= 30’ and income = ‘medium’ and age = ‘ 9’ then buys_computer = ‘no’ • If ‘age <= 30’ and income = ‘medium’ and age = ‘ 10’ then buys_computer = ‘no’ • If ‘age <= 30’ and income = ‘medium’ and age = ‘ 11’ then buys_computer = ‘no’ • If ‘age <= 30’ and income = ‘medium’ and age = ‘ 12’ then buys_computer = ‘no’ Due to the missing value in training dataset, the accuracy of prediction decreases and becomes “ 66. 7%” Discover only those rules which contain support (frequency) greater >= 1

Entropy-Based Discretization • Given a set of samples S, if S is partitioned into two intervals S 1 and S 2 using boundary T, the entropy after partitioning is • Where pi is the probability of class i in S 1, determined by dividing the number of samples of class i in S 1 by the total number of samples in S 1.

Entropy-Based Discretization • The boundary that minimizes the entropy function over all possible boundaries is selected as a binary discretization. • The process is recursively applied to partitions obtained until some stopping criterion is met, e. g. ,

Example 1 ID Age Grade 1 21 F 2 22 F 3 24 P 4 25 F 5 27 P 6 27 P 7 27 P 8 35 P 9 41 P • Let Grade be the class attribute. Use entropy-based discretization to divide the range of ages into different (22+24) / 2 = 23 discrete intervals. • There are 6 possible boundaries. They are 21. 5, 23, 24. 5, (21+22) / 2 = 21. 5 26, 31, and 38. • Let us consider the boundary at T = 21. 5. Let S 1 = {21} Let S 2 = {22, 24, 25, 27, 27, 35, 41}

Example 1 (cont’) ID Age 1 2 3 4 5 6 7 8 9 21 22 24 25 27 27 27 35 41 F F P P P Grade • The number of elements in S 1 and S 2 are: |S 1| = 1 |S 2| = 8 • The entropy of S 1 is • The entropy of S 2 is

Example 1 (cont’) • Hence, the entropy after partitioning at T = 21. 5 is

Example 1 (cont’) • The entropies after partitioning for all the boundaries are: T = 21. 5 = E(S, 21. 5) T = 23 = E(S, 23) . . T = 38 = E(S, 38) Now recursively apply entropy discretization upon both partitions Select the boundary with the smallest entropy Suppose best is T = 23 ID Age Grade 1 2 3 4 5 6 7 8 9 21 22 24 25 27 27 27 35 41 F F P P P

Chi. Merge (Kerber 92) • This discretization method uses a merging approach. • Chi. Merge’s view: – First sort the data on the basis of attribute (which is being descretize). – List all possible boundaries or intervals. In case of last example there were 6 boundaries, 0, 21. 5, 23, 24. 5, 26, 31, and 38. – For all two near intervals, calculate 2 class independent test. • • {0, 21. 5} and {21. 5, 23} and {23, 24. 5}. . – Pick the best 2 two near intervals and merge them.

Chi. Merge -- The Algorithm Compute the 2 value for each pair of adjacent intervals Merge the pair of adjacent intervals with the lowest 2 value ¸ Repeat and until 2 values of all adjacent pairs exceeds a threshold

Chi-Square Test Class 1 Class 2 Σ Int 1 o 12 R 1 Int 2 o 21 o 22 R 2 Σ C 2 N C 1 oij = observed frequency of interval i for class j eij = expected frequency (Ri * Cj) / N

Chi. Merge Example Data Set Sample: F K 1 2 3 4 5 6 7 8 9 10 11 12 1 3 7 8 9 11 23 37 39 45 46 59 1 2 1 1 1 2 2 1 1 1 • Interval points for feature F are: 0, 2, 5, 7. 5, 8. 5, 10, etc.
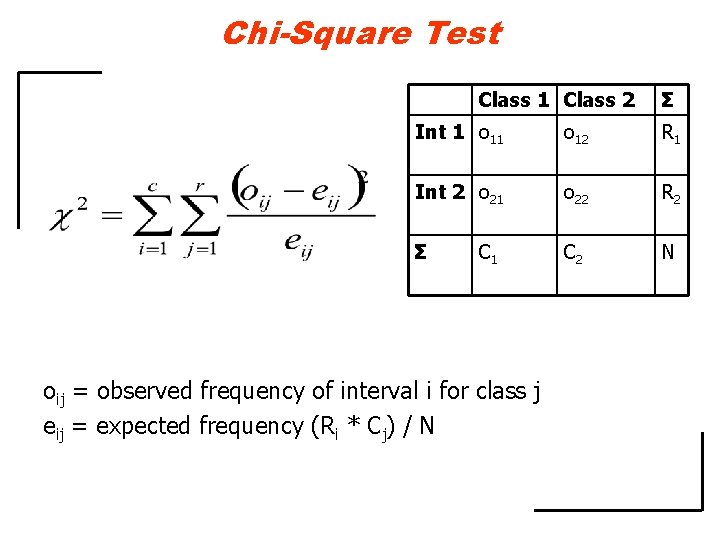
![Chi Merge Example cont 2 was minimum for intervals 7 5 8 5 Chi. Merge Example (cont. ) 2 was minimum for intervals: [7. 5, 8. 5]](https://slidetodoc.com/presentation_image_h/31c2a2a2eb32b5dc60b7e797c1e636d4/image-17.jpg)
Chi. Merge Example (cont. ) 2 was minimum for intervals: [7. 5, 8. 5] and [8. 5, 10] K=1 K=2 Interval [7. 5, 8. 5] A 11=1 A 12=0 R 1=1 Interval [8. 5, 9. 5] A 21=1 A 22=0 R 2=1 C 1=2 C 2=0 N=2 Based on the table’s values, we can calculate expected values: E 11 = 2/2 = 1, oij = observed frequency of E 12 = 0/2 0, E 21 = 2/2 = 1, and interval i for class j E 22 = 0/2 0 e = expected frequency (R * C ) ij / N and corresponding 2 test: 2 = (1 – 1)2 / 1 + (0 – 0)2 / 0. 1 + (1 – 1)2 / 1 + (0 – 0)2 / 0. 1 = 0. 2 For the degree of freedom d=1, and 2 = 0. 0 < 2. 706 ( MERGE !) i j
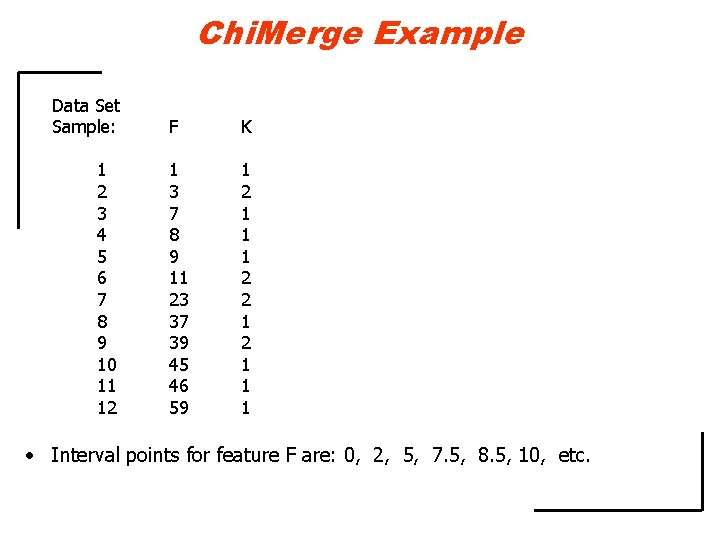
![Chi Merge Example cont Additional Iterations K1 K2 Interval 0 7 5 A Chi. Merge Example (cont. ) Additional Iterations: K=1 K=2 Interval [0, 7. 5] A](https://slidetodoc.com/presentation_image_h/31c2a2a2eb32b5dc60b7e797c1e636d4/image-18.jpg)
Chi. Merge Example (cont. ) Additional Iterations: K=1 K=2 Interval [0, 7. 5] A 11=2 A 12=1 R 1=3 Interval [7. 5, 10] A 21=2 A 22=0 R 2=2 C 1=4 C 2=1 N=5 E 11 = 12/5 = 2. 4, E 12 = 3/5 = 0. 6, E 21 = 8/5 = 1. 6, and E 22 = 2/5 = 0. 4 2 = (2 – 2. 4)2 / 2. 4 + (1 – 0. 6)2 / 0. 6 + (2 – 1. 6)2 / 1. 6 + (0 – 0. 4)2 / 0. 4 2 = 0. 834 For the degree of freedom d=1, 2 = 0. 834 < 2. 706 (MERGE!)

Chi. Merge Example (cont. ) A 11=4 A 21=1 K=2 A 12=1 A 22=3 C 1=5 C 2=4 N=9 K=1 Interval [0, 10. 0] Interval [10. 0, 42. 0] R 1=5 R 2=4 E 11 = 2. 78 E 12 =2. 22 E 21 = 2. 22 E 22 = 1. 78 and 2 = 2. 72 > 2. 706 (NO MERGE !) Final discretization: [0, 10], [10, 42], and [42, 60]

References – Text book of Jiawei Han and Micheline Kamber, “Data Mining: Concepts and Techniques”, Morgan Kaufmann Publishers, August 2000. (Chapter 3). – Data Mining: Concepts, Models, Methods, and Algorithms by Mehmed Kantardzic John Wiley & Sons 2003. (Chapter 3).