Dalla macchina alla rete reti LLC Dalla macchina

Dalla macchina alla rete: reti LLC

Dalla macchina alla rete • Per realizzare una macchina sequenziale è necessario – Codificare gli insiemi I, S, O con variabili di commutazione – Realizzare le funzioni d ed w con reti combinatorie • Ipotizzare il comportamento temporale delle variabili di ingresso/uscita – Ogni circuito digitale risponde ai nuovi valori di ingresso producendo la nuova uscita in modo stabile solo un tempo di ritardo d durante il quale sono esauriti tutti i transitori – Considereremo solo la realizzazione di reti di tipo LLC (Level Clocked)

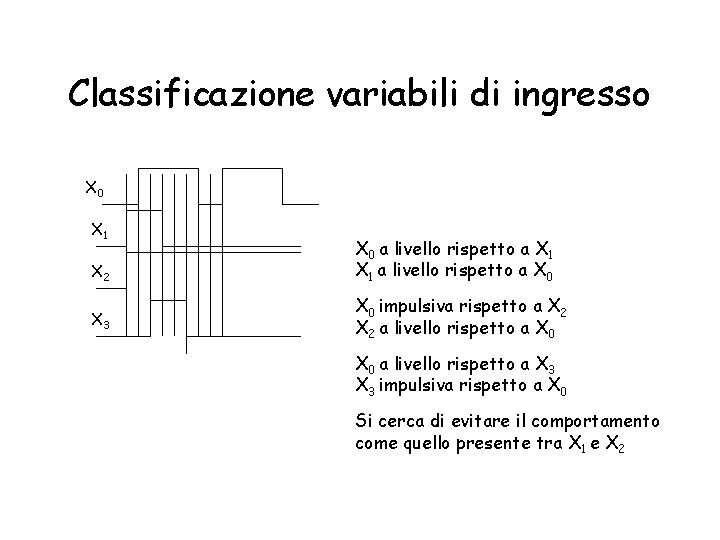
Classificazione variabili di ingresso X 0 X 1 X 2 X 3 X 0 a livello rispetto a X 1 a livello rispetto a X 0 impulsiva rispetto a X 2 a livello rispetto a X 0 a livello rispetto a X 3 impulsiva rispetto a X 0 Si cerca di evitare il comportamento come quello presente tra X 1 e X 2

Dalla macchina alla rete • x 1, x 2, . . , xn variabili di ingresso a livelli – 2 n |I| • z 1, x 2, . . , zm variabili di uscita a livelli – 2 m |O| • y 1, y 2, . . , yk variabili di stato – 2 k |S| • Variabile impulsiva, ck, che ha lo scopo di far commutare lo stato – ck=0 => (x 1, x 2, . . , xn) = i 0 (carattere “spazio”, i 0 I) – ck=1 => (x 1, x 2, . . , xn) = i I

Reti LLC • La rete sequenziale lavora con le seguenti ipotesi: – Variabili d’ingresso di tipo a livello (ossia il valori in ingresso rimangono fissi per un periodo T sufficientemente lungo per far assumere all’uscita il nuovo valore di regime, ossia T>d) – Variabili di uscita a livello – Segnale di abilitazione “positive or negative edge trigger”, o a livello (in quest’ultimo caso la variabile di commutazione deve essere pari ad 1 per un periodo di tempo sufficiente per far commutare i flip-flop, ma inferiore al minimo tempo di commutazione dei circuiti combinatori che calcolano lo stato successivo, altrimenti si potrebbero avere più commutazioni)

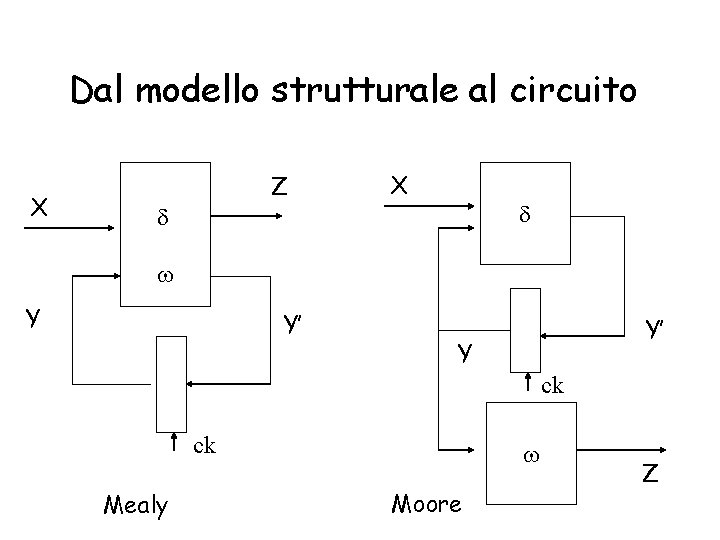
Dal modello strutturale al circuito X Z d X d w Y Y’ Y’ Y ck ck Mealy w Moore Z

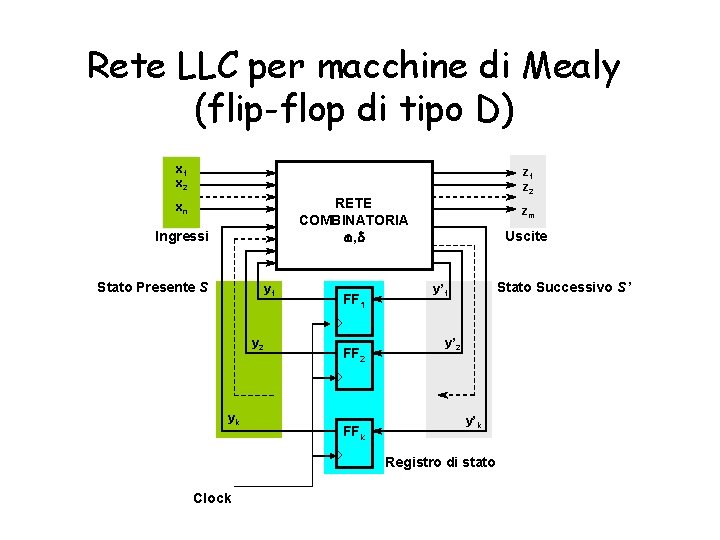
Rete LLC per macchine di Mealy (flip-flop di tipo D) x 1 x 2 z 1 z 2 RETE COMBINATORIA w, d xn Ingressi Stato Presente S y 1 y 2 yk FF 1 FF 2 FFk zm Uscite Stato Successivo S’ y’ 1 y’ 2 y’k Registro di stato Clock

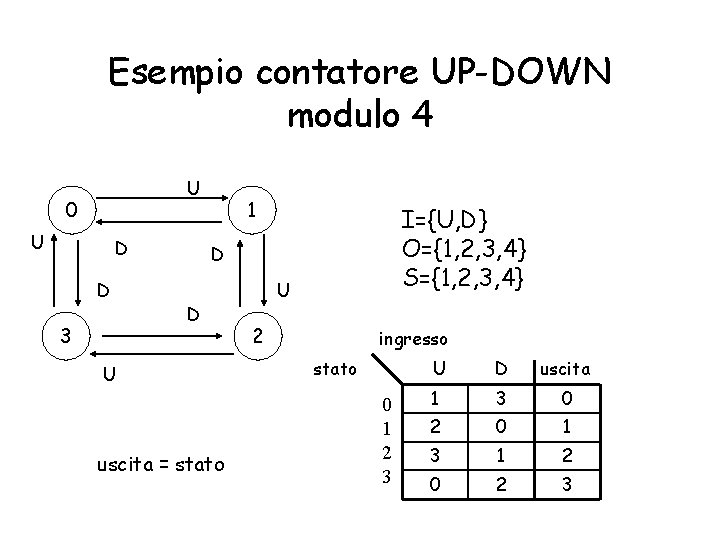
Esempio contatore UP-DOWN modulo 4 U 0 U D D 3 1 I={U, D} O={1, 2, 3, 4} S={1, 2, 3, 4} D D U uscita = stato U 2 ingresso stato 0 1 2 3 U D uscita 1 3 0 2 0 1 3 1 2 0 2 3

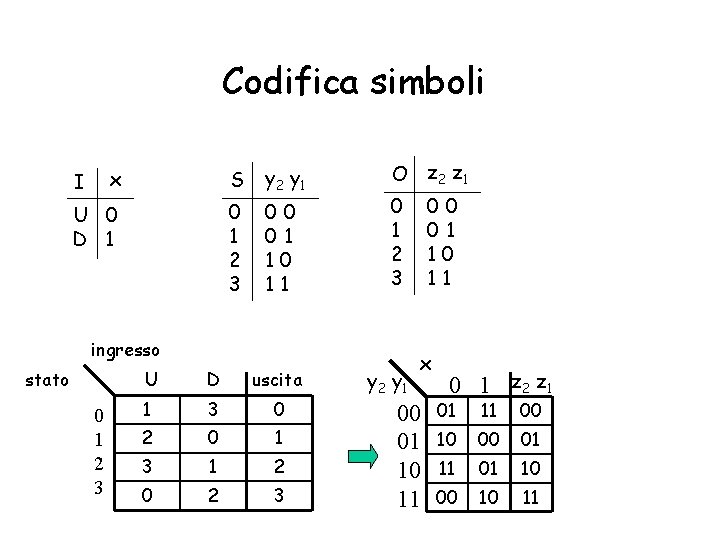
Codifica simboli x S y 2 y 1 U 0 D 1 0 1 2 3 00 01 10 11 I O z 2 z 1 0 1 2 3 ingresso stato 0 1 2 3 U D uscita 1 3 0 2 0 1 3 1 2 0 2 3 y 2 y 1 00 01 10 11 x 00 01 10 11 0 1 z 2 z 1 01 11 00 10 00 01 11 01 10 00 10 11

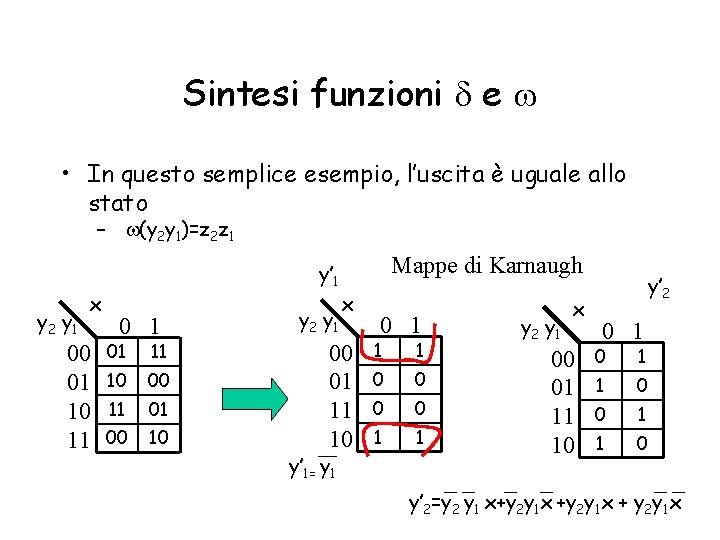
Sintesi funzioni d e w • In questo semplice esempio, l’uscita è uguale allo stato – w(y 2 y 1)=z 2 z 1 y 2 y 1 x 00 01 10 11 y’ 1 01 11 10 00 11 01 00 10 y 2 y 1 Mappe di Karnaugh x 00 01 11 10 y’ 1= y 1 0 1 1 1 0 0 1 1 y 2 y 1 x 00 01 11 10 y’ 2 0 1 1 0 y’ 2=y 2 y 1 x+y 2 y 1 x + y 2 y 1 x

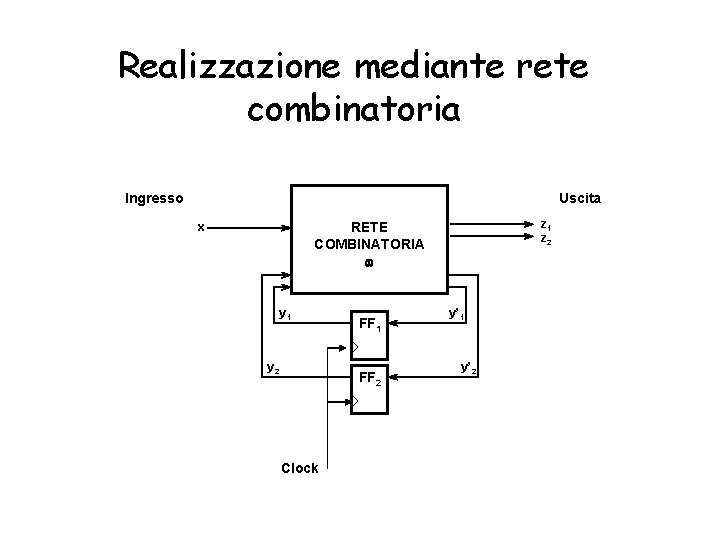
Realizzazione mediante rete combinatoria Ingresso Uscita z 1 z 2 RETE COMBINATORIA w x y 1 y 2 FF 1 FF 2 Clock y’ 1 y’ 2

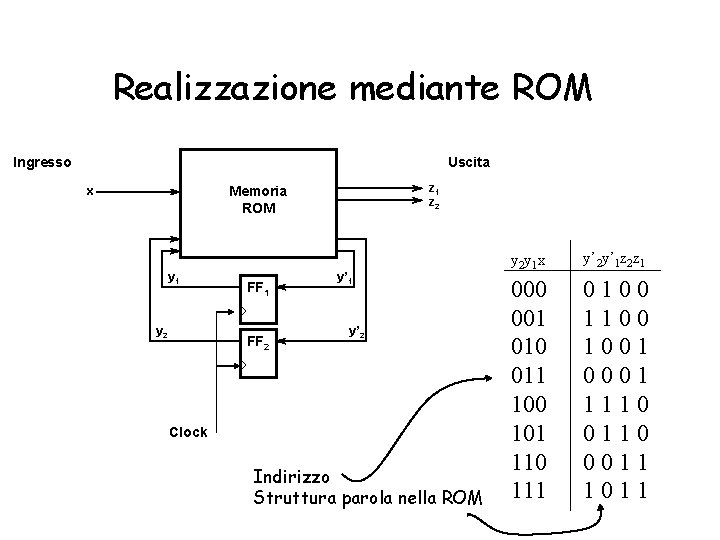
Realizzazione mediante ROM Ingresso Uscita z 1 z 2 Memoria ROM x y 1 y 2 FF 1 FF 2 y’ 1 y’ 2 Clock Indirizzo Struttura parola nella ROM y 2 y 1 x y’ 2 y’ 1 z 2 z 1 000 001 010 011 100 101 110 111 0100 1001 0001 1110 0011 1011