Cursul 6 Paradigma algoritmilor greedy continuare Studii de

Cursul 6 Ø Paradigma algoritmilor “greedy” (continuare) ð Studii de caz • arborele partial de cost minim • secventializarea activitatilor ð Prezentarea formala a paradigmei

Arborele partial de cost minim - formulare Ø instanta: ð un graf ponderat (G, w), G = (V, E), w : E R ð arbore = graf conex fara cicluri ð subgraf partial: G’ = (V, E’) cu E’ E ð arbore partial = subgraf partial + arbore ð costul unui arbore partial este w(G’) = {i, j} E’ w({i, j}) Ø iesire: ð un arbore partial de cost minim

Arborele partial de cost minim – algoritm generic procedure APCM(G, w) begin A E 1 E while ((V, A) nu este arbore partial) do alege din E 1 o muchie {i, j} “sigura” pentru A E 1 - {{i, j}} A A {{i, j}} end ð muchia {i, j} “sigura” pentru A A {{i, j}}este submultime a unui arbore partial de cost minim

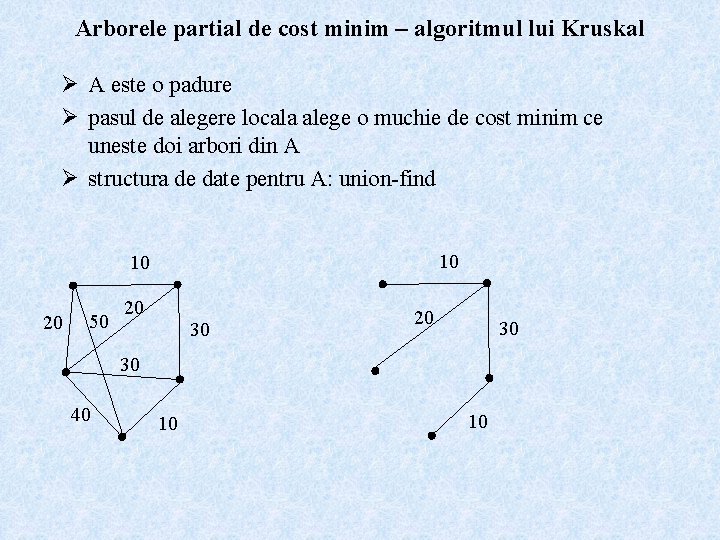
Arborele partial de cost minim – algoritmul lui Kruskal Ø A este o padure Ø pasul de alegere locala alege o muchie de cost minim ce uneste doi arbori din A Ø structura de date pentru A: union-find 10 10 20 50 20 30 30 40 10 10

Arborele partial de cost minim – algoritmul lui Kruskal (cont) procedure APCM_Kruskal(G, w) begin A for each i in V do single(i) sorteaza E crescator dupa w for each {i, j} in E in ordine crescatoare do if (find(A, i) find(A, j) then union(A, i, j) end

Algoritmul lui Kruskal - formalizare Ø S = multimea de muchii Ø X C(S) daca X este padure Ø alegere locala: ð adauga la B muchia {i, j} de cost minim a. i. • {i, j} uneste doi arbori din (B {{i, j}} C(S) ) • {i, j} de cost minim peste muchiile care satisfac proprietatea de mai sus Ø proprietatea de substructura optima

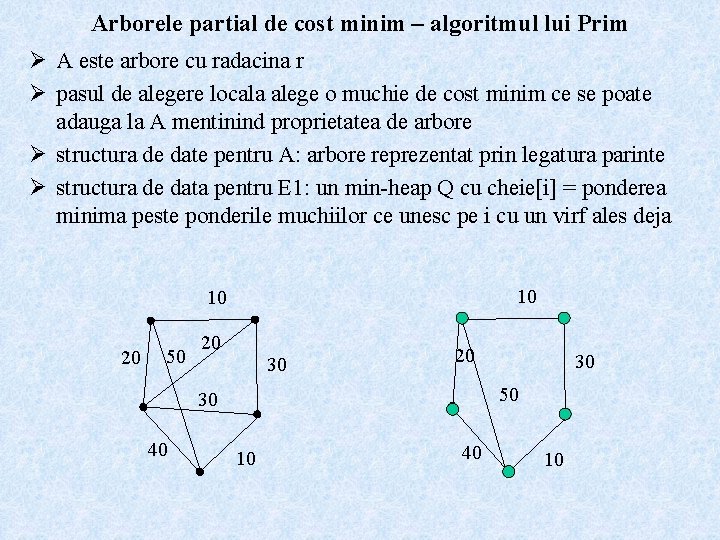
Arborele partial de cost minim – algoritmul lui Prim Ø A este arbore cu radacina r Ø pasul de alegere locala alege o muchie de cost minim ce se poate adauga la A mentinind proprietatea de arbore Ø structura de date pentru A: arbore reprezentat prin legatura parinte Ø structura de data pentru E 1: un min-heap Q cu cheie[i] = ponderea minima peste ponderile muchiilor ce unesc pe i cu un virf ales deja 10 10 20 50 20 30 20 50 30 40 30 10 40 10

Arborele partial de cost minim – algoritmul lui Prim procedure APCM_Prim(G, w, r) begin Q V for fiecare i in Q do cheie[i] cheie[r] 0; parinte[r] -1 while (Q ) do citeste(Q, i); elimina(Q) for (fiecare j in lista. De. Adiac[i]) do if (j Q and w({i, j}) < cheie[j]) then parinte[j] = i; cheie[j] w({i, j}) end

Algoritmul lui Kruskal - formalizare Ø S = multimea de muchii Ø X C(S) daca X este arbore Ø alegere locala: ð adauga la B muchia {i, j} de cost minim a. i. • B {{i, j}} arbore ( C(S) ) • {i, j} de cost minim peste muchiile care satisfac proprietatea de mai sus Ø proprietatea de substructura optima

Secventializarea optima a activitatilor: formulare Ø Intrare: ð n activitati 0, 1, 2, …, n-1 ð fiecare unitate dureaza o unitate de timp ð realizarea activitatii i aduce profitul p(i) > 0 ð activitatea i trebuie terminata la termenul limita d(i) (deadline) Ø Iesire ð o lista liniara s = (s(0), …, s(k-1)) de activitati a. i. • orice activitate s(i) este realizata in termen, d(s(i)) i+1 • profitul este maxim

Secventializarea optima a activitatilor: exemplu i 0 1 2 3 d(i) 2 3 1 2 p(i) 20 35 35 25 Ø o solutie posibila: (0, 3, 1) cu profitul 20 + 25 + 35 = 80 ð d(0) = 2 1, d(3) = 2 2, d(1) = 3 3 Ø o alta solutie posibila: (2, 3, 1) cu profitul 35 + 25 + 35 = 95 ð d(2) = 1 1, d(3) = 2 2, d(1) = 3 3 Ø exista vreo solutie mai buna?

Secventializarea optima a activitatilor: model mat. Ø solutie acceptabila: s = (s(0), …, s(k-1)) a. i. ( i) d(s(i)) i+1 (orice activitate este realizata in timp) Ø solutia optima: s* a. i. s* aduce profit maxim peste solutiile acceptabile i p(s*(i)) = max{ i p(s(i)) | s acceptabila} Ø reordonarea unei solutii acceptabile in ordinea crescatoare a termenelor limita produce tot o solutie acceptabila i 0 1 2 3 d(i) 2 3 3 2 (2, 0, 1) solutie acceptabila (0, 2, 1) solutie acceptabila Rezulta ca putem reprezenta o solutie acceptabila ca o multime: {0, 1, 2}; secventa acceptabila se obtine ordonand multimea dupa termenii limita

Secventializarea optima a activitatilor: model mat. Ø criteriul de alegere locala: B B {i} unde i este activitatea de profit maxim a. i. B {i} este solutie acceptabila Ø Teorema. Daca B este determinata de algoritmul greedy, atunci orice secventializare acceptabila a lui B este optima. i 0 1 2 3 d(i) 2 3 1 2 p(i) 20 35 35 25 B=Ø B = {1} B = {1, 2, 3} s = (2, 3, 1) Ideea de demonstratie: Fie B’solutie optima. Daca B B’ si B are r elemente comune cu B’, se construieste o alta solutie optima B’’ din B’ a. i. B si B’’ au r+1 elemente comune.

Secventializarea optima a activitatilor: model mat. Ø S = multimea activitatilor Ø C(S): X C(S) daca X este solutie acceptabila (admite o secventializare acceptabila) Ø proprietatea de alegere locala: Ø proprietatea de substructura optima:

Algoritmi “greedy” – formulare matematica Ø modelul matematic ð S multime de stari, C colectie de submultimi ale lui S ð axioma de accesibilitate (AA) X C: X ( x X: X {x} C) ð sistem accesibil: (S, C) ð X este extensibila daca exista y S – C a. i. X {y} C ð baza: X C maximala ð presupunere: B, B’ baze (B B’ B)

Algoritmi “greedy” – formulare matematica (continuare I) Ø modelul matematic (continuare) ð clasa de probleme: • intrare: S, C, f : C R (functia obiectiv) • iesire: o baza B cu f(B) = optim{f(X) | X baza in C} ð alegere “greedy”: alege x dintre elementele nealese a. i. f(B {x}) este optim peste {f(B {y}) | y neales si (B {y}) C} (*)

Algoritmi “greedy” – formulare matematica (continuare II) procedure alg. Greedy(S, C, f, B) begin S 1 S B while (B este extensibila) do alege x din S 1 conf. crit. (*) S 1 – {x} B B {x} end

Algoritmi “greedy” – formulare matematica (continuare III) Ø un caz cind alegerea “greedy” produce optim global: ð (S, C) este matroid: • AA este inlocuita cu proprietatea de ereditate: X C, X ( x X: X {x} C) ð are loc proprietatea de interschimbare (PI): X, Y C, |X| < |Y| ( y Y-X: X {y} C) ð (S, C) este matroid ponderat: • f este o pondere: f : S R , f(X) = (f(x) | x X) • optim = max • alegere “greedy”: alege x a. i. f(x) = max{f(y) | y in S B, B {y}) C}

Algoritmi “greedy” – formulare matematica (continuare IV) Teorema: Algoritmul “greedy” determina o submultime optima daca (S, C) este matroid ponderat. Ø Demonstratie: ð x de pondere maxima ð Fapt: exista o solutie optima B care contine pe x • fie B’ o solutie optima; pp ca x nu e in B’ • luam B ={x}; apoi utilizam PI si adaugam la B elem. din B’ a. i. B = B’ – {y} {x} • B este optima ð S’ = { y | {x, y} C }, C’ = {X | X {x} C} ð daca B este solutie pentru (S, C) care contine x, atunci B – {x} este solutie optima pentru (S’, C’)