Cursul 5 Paradigma algoritmilor greedy Prezentarea generala a

Cursul 5 Ø Paradigma algoritmilor “greedy” ð Prezentarea generala a paradigmei ð Studii de caz • memorarea programelor • rucsac (varianta continua) • arbori Huffman • arborele partial de cost minim

Algoritmi “greedy” - ingrediente Ø probleme de optim Ø proprietatea de alegere locala (“greedy”) ð solutia de optim global poate fi obtinuta facind alegeri optime locale (“greedy”) ð alegerea optima locala curenta poate depinde de alegerile de pina atunci dar nu si de cele viitoare ð trebuie demonstrat ca alegerile optime locale conduc la obtinerea optimului global Ø proprietatea de substructura optima ð solutia optima a problemei contine solutiile optime ale subproblemelor

Algoritmi “greedy” – o prima formalizare Ø S – o multime de intrari Ø C(S) ð obiectele din C(S) sunt submultimi ale lui S ð operatii: X {x}, X – {x} Ø Problema ð Intrare: S, f : C(S) R ð Iesire: B obiect maximal din C(S) care optimizeaza f Ø B este construita incremental Ø Alegerea locala ð alege x a. i. B {x} C(S) ð x defineste un optim local Ø proprietatea de substructura optima ð fie x primul ales de alg. greedy ð solutia problemei initiale include solutia subproblemei coresp. lui S’ = S – {x}, C(S’) = {B S’ | B {x} C(S)}, f restrictionata la C(S’)

Memorarea eficienta a programelor - formulare Ø instanta ð n obiecte 0, 1, . . . , n-1 de marimi (lungimi) L 0, L 1 , . . . , Ln-1 ð presupunem cele n obiecte asezate intr-o lista liniara in ordinea ( (0), . . . , (n-1)) ð timpul de regasire a obiectului de pe pozitia k este t(k) = i=0, k L (i) ð timpul mediu de regasire este TM( ) = 1/n k=0, n-1 t(k) Ø iesire ð o asezare a obiectelor in lista a. i. timpul mediu de regasire sa fie minim

Memorarea eficienta a programelor – algoritm “greedy” Ø exemplu ð L = (40, 10, 60, 30) ð TM(id) = (40 + 50 + 110 + 140)/4 = 340/4 = 85 ð = (1, 3, 0, 2) ð TM( ) = (10 + 40 + 80 + 140) = 270/4 < 85 Ø algoritm “greedy”: alege la pasul curent un obiect neales inca de lungime minima ð alegerea “greedy” duce la obtinerea optimului global • o permutarea a. i. i < j si L (i) > L (j) • ’ = (i, j) ( inmultit cu transpozitia (i, j)) • TM( ’) < TM( ) • rezulta ca este optima daca ( i, j) i < j L (i) L (j) • permutarea calculata de alg. greedy satisface ac. prop. ðproprietatea de substructura optima (? ) ð timp: O(n log n) ð spatiu suplimentar: O(1)

Memorarea eficienta a programelor – algoritm “greedy”, formal Ø S = {(i, j) | 0 i, j < n} Ø X C(S) daca: ( (i, j), (i’, j’) X) i = i’ j = j’ Ø alegerea locala: ð(k, i) a. i. k este prima pozitie libera si L(i) minim peste obiectele nealese ðB B {(k, i)} Ø in final B descrie permutarea care ordoneaza obiectele crescator dupa marime Ø proprietatea de substructura optima ðpermutarea “include” permutarea ce ordoneaza crescator dupa marime obiectele {0, 1, …, n-1} – (0) (eliminarea celui mai mic obiect)

Problema rucsacului (varianta continua): formulare Ø instanta: ð n obiecte 0, 1, . . . , n-1 de dimensiuni (greutati) w 0, w 1, . . . , wn-1 ð un rucsac de capacitate M ð introducerea in rucsac a unei parti fractionare xi din obiectul i aduce un profit xi pi ð profitul total adus de alegerile x 0, . . . , xn-1 este i=0, n-1 xipi Ø iesire: ð o alegere pentru care profitul adus este maxim

Problema rucsacului: solutie “greedy” care nu-i OK Ø la pasul curent alege obiectul cu profitul pi cel mai mare ð contraxemplu: • n = 3, p = (3, 4, 6), w = (6, 4, 8), M = 10 • profitul = 8 cu alegerea (0, ½, 1)

Problema rucsacului: solutie “greedy” OK Ø la pasul curent ð alege obiectul ce aduce profit maxim pe unitatea de greutate (pi/wi) ð daca este loc suficient in rucsac, obiectul se introduce in totalitate (xi = 1) ð altfel obiectul este introdus partial (maxim din cit se poate, 0 xi < 1) si procesul de alegere se opreste Ø exemplu (continuare): ð p/w = (3/6, 4/4, 6/8) ð profitul = 17/2 cu alegerea (0, 1, 6/8) Teorema Solutia calculata de algoritmul “greedy” este optima ð demonstratie Ø timp: O(n log n) Ø spatiu suplimentar: O(n)

Problema rucsacului: solutie “greedy”, formalizare Ø S = {(i, x) | 0 i < n, x [0, 1]} Ø X C(S) daca: ( (i, x), (i’, x’) X) i = i’ x = x’ (xwi | (i, x) X) M Ø alegerea locala: ð(i, xi) a. i. i aduce profit maxim pe unitatea de greutate si x cantit maxima ce incape in rucsac ðB B {(i, xi)} Ø proprietatea de substructura optima ðsolutia x include solutia x’corespunzatoare subproblemei P’ obtinuta din P prin eliminarea obiectului i cu profit maxim pe unitatea de greutate si M’ = M – wi

Coduri Huffman Ø Coduri liber (independent) de prefix optime ð instanta • n mesaje M 0, M 1, . . . , Mn-1 cu frecventele f 0, f 1, . . . , fn-1 • cod(Mi) {0, 1}*, i, j: i j cod(Mi) nu este prefix a lui cod(Mj) • lungimea medie a codificarii = 1/n i=0, n-1 (|cod(Mi)|fi) ð iesire • o codificare cu lungimea medie minima

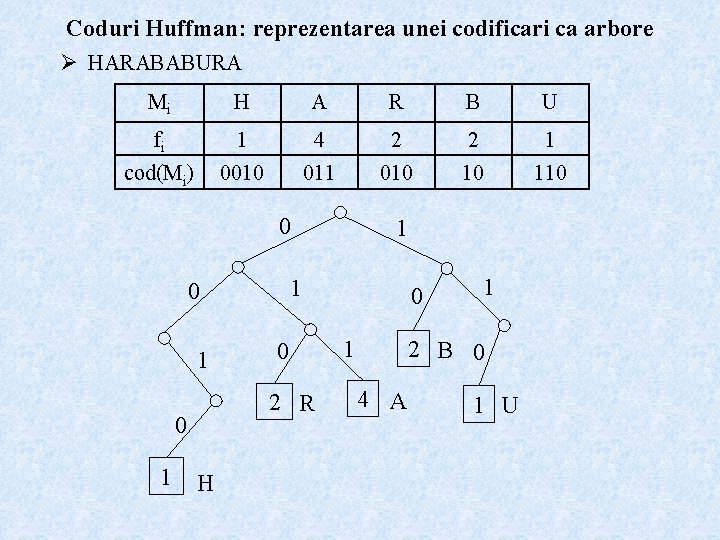
Coduri Huffman: reprezentarea unei codificari ca arbore Ø HARABABURA Mi H A R B U fi 1 4 2 2 1 cod(Mi) 0010 011 010 10 110 0 1 1 0 2 R 0 H 1 0 1 1 2 B 0 4 A 1 U

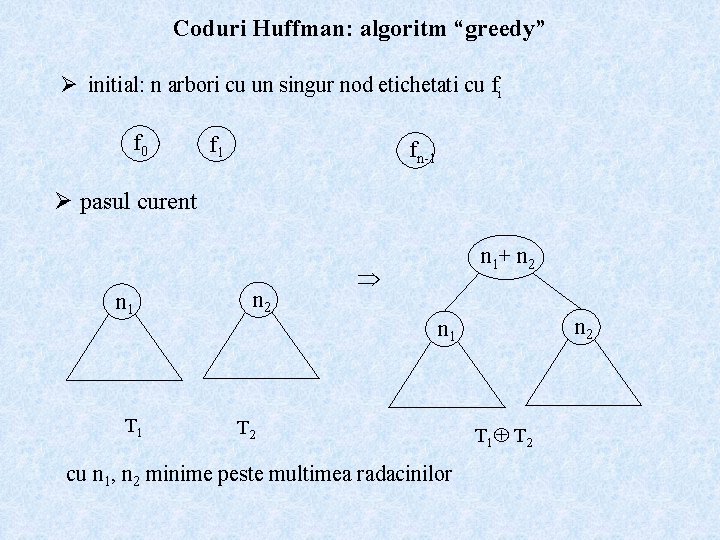
Coduri Huffman: algoritm “greedy” Ø initial: n arbori cu un singur nod etichetati cu fi f 0 f 1 fn-1 Ø pasul curent n 1 T 1 n 2 n 1+ n 2 n 1 T 2 cu n 1, n 2 minime peste multimea radacinilor T 1 T 2

Proprietati ale codurilor Huffman Lema Fie cod o codificare optima. Daca fi < fj atunci |cod(Mi)| |cod(Mj)| (mesajele cu frecvente mai mari au lungimile codurilor mai mici) ð demonstratie Lema Orice codificare optima poate fi transformata intr-o codificare Huffman cu aceeasi lungime medie. ð demonstratie

Coduri Huffman: algoritm “greedy”, formalizare Ø S – cea mai mica multime de arbori construita astfel: ð fi S ð T 1, T 2 S T 1 T 2 S Ø X C(S) daca: ( T X) T = fi sau ( T 1, T 2 X) T = T 1 T 2 X este finita f(X) = max{suma_ponderata(T) | T S} Ø alegere locala B = B {T 1 T 2}, T 1, T 2 cu radacini minime in B Ø proprietatea de substructura optima ð solutia problemei coresp. intrarii f 0, f 1, . . . , fn-1 “include” solutia subproblemei coresp. intrarii f 0 + f 1, . . . , fn-1, unde f 0, f 1 sunt minime

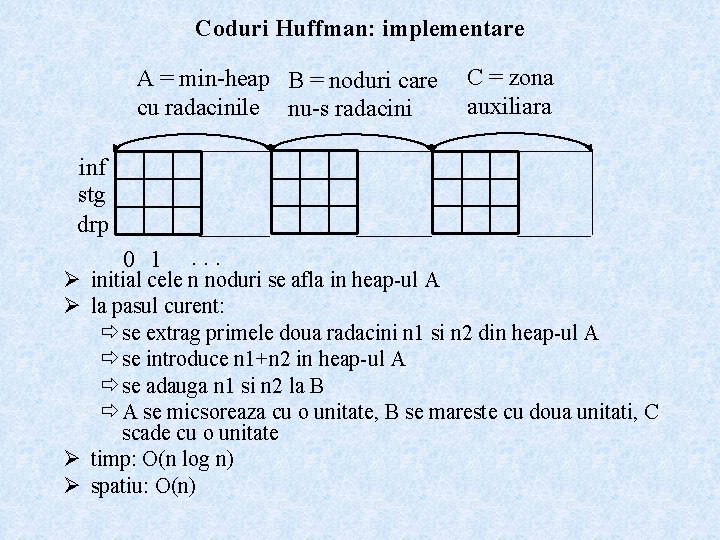
Coduri Huffman: implementare A = min-heap B = noduri care cu radacinile nu-s radacini C = zona auxiliara inf stg drp 0 1 . . . Ø initial cele n noduri se afla in heap-ul A Ø la pasul curent: ð se extrag primele doua radacini n 1 si n 2 din heap-ul A ð se introduce n 1+n 2 in heap-ul A ð se adauga n 1 si n 2 la B ð A se micsoreaza cu o unitate, B se mareste cu doua unitati, C scade cu o unitate Ø timp: O(n log n) Ø spatiu: O(n)