Curs 8 Paradigma Programare dinamica Studii de caz

Curs 8 Ø Paradigma Programare dinamica ð Studii de caz • distanta intre siruri • subsecventa crescatoare de lungime maxima • Prezentarea formala a paradigmei

Distanta intre siruri – problema Ø instanta ð doua siruri a si b de lungime n ð asupra lui a se pot face operatiile: • modificare: M(i, c) daca ai c • stergere: S(i) • inserare: I(i, c) Ø iesire ð o secventa de operatii de lungime minima care transforma sirul a in b Ø exemplu ð a = “armata”, b = “camara” ð “armata” “amata” “camara” ð d[“armata”, “camara”] = 3

Distanta intre siruri – propretati Ø ordinea operatiilor intr-o secventa optima nu are importanta ð “armata” “amata” “camara” ð “armata” “amara” “camara” ð “armata” “camata” “camara” ð “armata” “carmara” “camara” ð “armata” “armara” “amara” “camara” ð “armata” “armara” “camara”

Distanta intre siruri – proprietati (cont. ) Ø exista o secventa optima in care sirurile intermediare au lungimea n Ø d[a, b] este o metrica: ð d[a, a] = 0 ð d[a, b] = d[b, a] ð d[a, c] d[a, b] + d[b, c]

Distanta intre siruri – model Ø stare: DES[i, j] = determinarea distantei minime intre subsirurile de lungime i si respectiv j Ø valoarea asociata unei stari: [i, j] Ø functia asociata unei stari: d[i, j] = d[a[1. . i], b[1. . j]] Ø decizie: ð presupunem ca b[j] se obtine prin stergere: DES[i, j] DES[i-1, j] ð presupunem ca b[j] se obtine prin modificare: DES[i, j] DES[i-1, j-1] ð presupunem ca a[i] se obtine prin inserare: DES[i, j] DES[i, j-1]

Distanta intre siruri – model (cont. ) Ø relatia de recurenta d[0, j] = j, d[i, 0] = i ( i, j) d[i, j] = min{d[i-1, j] + 1, d[i-1, j-1] + [i, j], d[i, j-1] + 1} [i, j] = if (a[i] = b[j]) then 0 else 1 Ø timp: ð calculului matricii d: O(n 2) ð determinarea secventei de operatii: O(n) Ø spatiu: O(n 2)

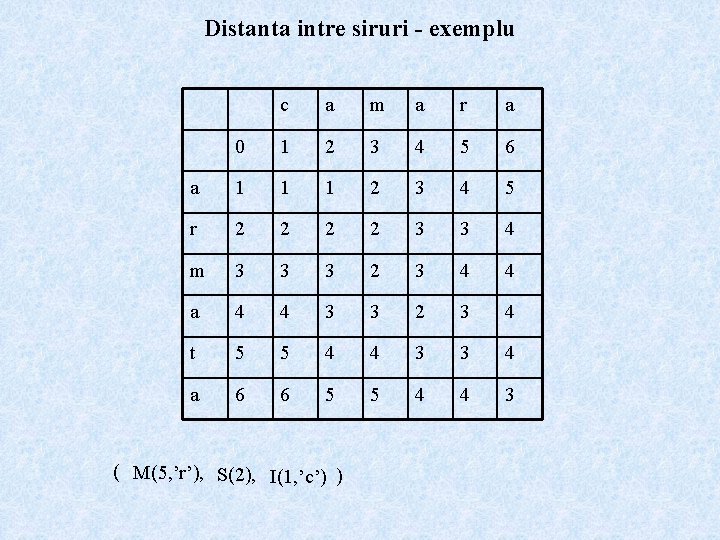
Distanta intre siruri - exemplu c a m a r a 0 1 2 3 4 5 6 a 1 1 1 2 3 4 5 r 2 2 3 3 4 m 3 3 3 2 3 4 4 a 4 4 3 3 2 3 4 t 5 5 4 4 3 3 4 a 6 6 5 5 4 4 3 ( M(5, ’r’), S(2), I(1, ’c’) )

Distanta intre siruri - variatii Ø alte operatii: ð transpozitia: schimba ordinea a doua caractere adiacente Ø distanta Levenshtein (de editare) ð sunt admise numai inserari, stergeri si inlocuiri ð toate operatiile au costul 1 Ø distanta Hamming ð sunt admise numai inlocuirile ð costul operatiei este 1 ð este finita ori de cate ori |a| = |b| Ø distanta “episodica” (episode distance) ð sunt admise numai inserari ð costul operatiei este 1 ð distanta este sau |b|-|a| sau

Distanta intre siruri - variatii Ø distanta data de cea mai lunga subsecventa ð sunt admise numai inserari si stergeri ð toate operatiile au costul 1 a = “amxbtycsnma” si b = “bancxstymcxn” “amxbtycsnma” “baxbtycsnma” “bancxbtycsnma” “bancxstycsnma” “bancxstymcnma” “bancxstymcxna” “bancxstymcxn” = b • (a, x, t, y, c, n) este subsecventa comuna • este cea mai lunga?

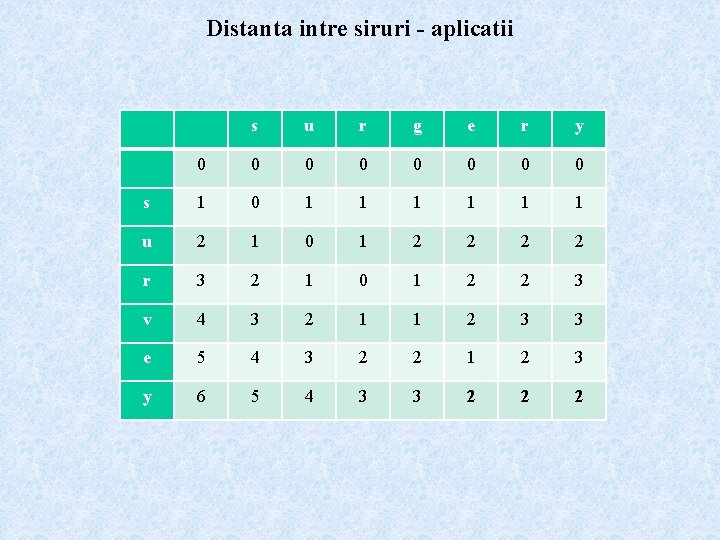
Distanta intre siruri - aplicatii Ø “matching” aproximativ peste siruri (aproximate string matching) ð problema: dat un text s de lungime n, un patern p de lungime m, o distanta d() intre siruri si un numar k, sa se determine pozitiile j din textul s astfel incat sa existe i cu d(p, s[i. . j]) k ð distanta Levenshtein: “string matching with k differences” ð distanta Hamming: “string matching with k missmatches” ð distanta episodica: “episode matching” (modeleaza cazul cand se cauta o secventa de evenimente intr-o perioada scurta de timp) ð cea mai lunga subsecventa comuna: exact ce spune numele ð procesul de cautare: • a = p, b = s • trebuie sa modificam alg. a. i. orice pozitie j din text este startul potential al unei potriviri; asta se realizeaza prin setarea d[0, j] = 0

Distanta intre siruri - aplicatii • • • calculul matricei se face pe coloane initial: d[i, 0] = i pentru i = 0, …, m se proceseaza textul caracter cu caracter presupunem ca la pasul curent se proceseaza sj coloanaj este actualizata: d[i, j] = if (pi = sj) then d[i-1, j-1] else 1 + min(d[i-1, j], d[i, j-1], d[i-1, j-1]) • pozitiile j pentru care d[m, j] k sunt raportate • de remarcat ca numai ultimele doua coloane sunt necesare

Distanta intre siruri - aplicatii s u r g e r y 0 0 0 0 s 1 0 1 1 1 u 2 1 0 1 2 2 r 3 2 1 0 1 2 2 3 v 4 3 2 1 1 2 3 3 e 5 4 3 2 2 1 2 3 y 6 5 4 3 3 2 2 2

Parallelizing

Subsecventa crescatoare maximala – problema Ø instanta ð o secventa de numere intregi a = (a 1, a 2, …, an) ð stergand cateva elemente din a se obtine o subsecventa ð o subsecventa pastreaza ordinea relativa a elementelor ð exemplu: • a = (9, 3, 15, 12, 7, 4, 13, 6, 8) • subsecventa: (3, 12, 7, 6) • subsecventa crescatoare: ( 3, 7, 13) Ø iesire: subsecventa crescatoare de lungime maxima Ø exemplu: exista o subsecventa crescatoare de lungime > 3? Ø cum se poate rezolva utilizand distanta de editare?

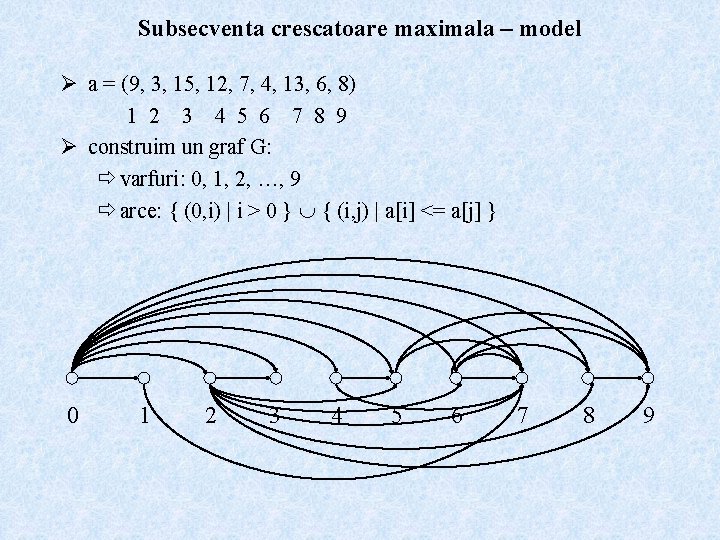
Subsecventa crescatoare maximala – model Ø a = (9, 3, 15, 12, 7, 4, 13, 6, 8) 1 2 3 4 5 6 7 8 9 Ø construim un graf G: ð varfuri: 0, 1, 2, …, 9 ð arce: { (0, i) | i > 0 } { (i, j) | a[i] <= a[j] } 0 1 2 3 4 5 6 7 8 9

Subsecventa crescatoare maximala – model Ø subsecventa crescatoare = drum in G Ø subsecventa crescatoare maximala = drum de lungime maxima in G Ø asociem o matrice de costuri: ð c[i, j] = 1 daca i < j si (a[i] <= a[j] sau i = 0) ð c[i, j] = - altfel Ø stare: SCM(i) = subproblema determinarii celui mai lung drum ce se termina in i Ø L[i] = valoarea optima pentru SCM(i) Ø PO implica L[i] = L[j] + c[j, i], j predecesorul lui i pe drumul optim Ø relatia de recurenta: ð L[0] = 0 ð L[i] = max { L[j] + c[j, i] | j < i }

Subsecventa crescatoare maximala – model Ø a = (9, 3, 15, 12, 7, 4, 13, 6, 8) 0 1 2 3 4 5 6 7 8 9 L = (0, 1, 1, 2, 2, 3, 3, 4) Ø extragerea solutiei: ð s[4] = 9 ð s[3] = 8 ð s[2] = 6 ð s[1] = 2 ð s[0] = 0 Ø timp de executie: O(n 2) Ø spatiu suplimentar: O(n)

Programare dinamica – prezentare formala Ø Modelul matematic ð probleme de optim • functia obiectiv: optim R(x 1, . . . , xn) • restrictii: g(x 1, . . . , xn) ? 0 ð decizie: d: s s’ ð unei stari s asociem o valoare z si o functie f(z) a. i. daca s corespunde starii initiale atunci f(z) = optim R(x 1, . . . , xn) ð politica: d 1: s 0 s 1, d 2: s 1 s 2, . . . , dn: sn-1 sn,

Programare dinamica – prezentare formala (cont. ) ð PO conduce la o relatie de recurenta: • daca – d: s s’ (sau d: s’ s) – z val. asociata lui s, T(z, y) val. asociata lui s’, – H algoritmul care calculeaza f(z) conform lui d, atunci, aplicind PO, obtinem f(z) = optimy H(z, y, f(T(z, y)))