CSC 444 Software Engineering Release Planning CSC 444

CSC 444 Software Engineering Release Planning CSC 444 F'07 Lecture 7 1

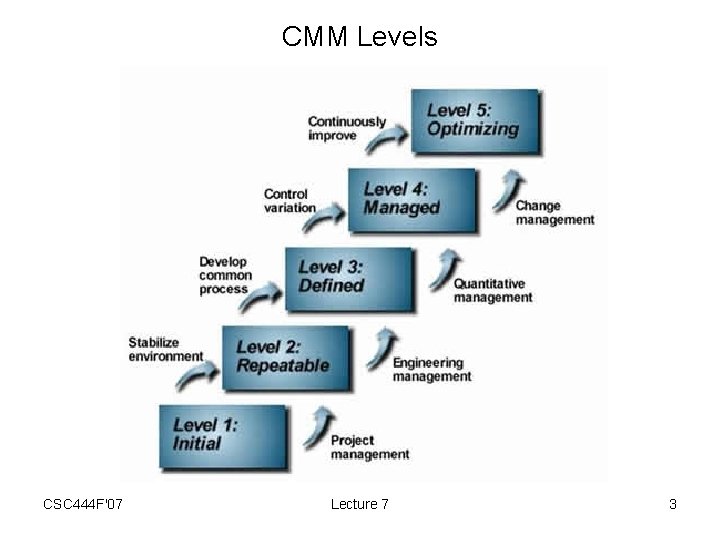
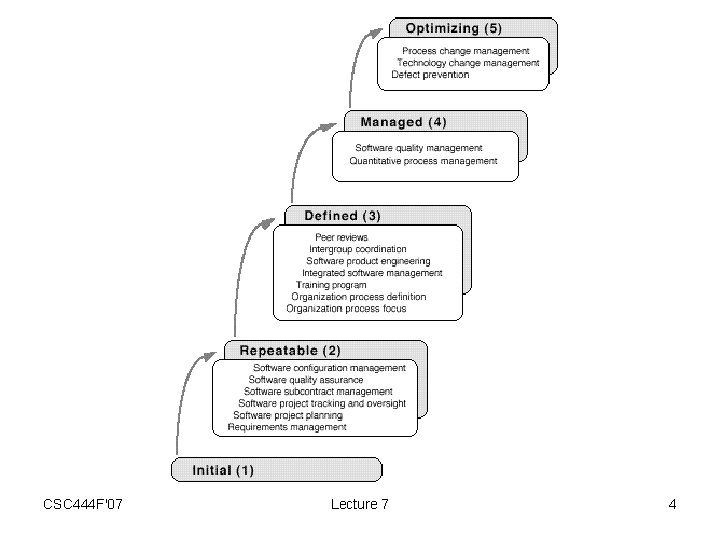
Capability Maturity Model • Developed at Carnegie-Melon Software Engineering Institute by Watts Humphrey. • Classifies an organization’s process maturity into 5 levels. – Each level is a group of practices. – The CMM is a roadmap for process improvement. – Should have substantially all practices in place for a lower level before proceeding to the next • Can be certified to a certain CMM level – Some similarities to • Malcolm Baldrige • ISO 9000 • Not universally agreed to be a good thing – But everyone agrees to pretend CSC 444 F'07 Lecture 7 2

CMM Levels CSC 444 F'07 Lecture 7 3

CSC 444 F'07 Lecture 7 4

Relationship to ISO 9000 • ISO 9000 – Set of quality standards – Subset relate to software development • In essence – Must document the process – Must maintain “quality records” • These are auditable to ensure the process is being carried out • The process can be anything CSC 444 F'07 Lecture 7 5

Relationship to Top 10 • Practices necessary to achieve CMM Level 2 (Repeatable). • With enough Level 3 (defined) added to attain ISO 9000. • With some Level 4 (quantitatively managed) sprinkled in where most effective: – – Defect arrival / departure rates Estimates versus actuals Metrics on process step completion Defect attribution CSC 444 F'07 Lecture 7 6

Planning • Most important aspect of CMM Level 2 • Common flaws: – Make no plans – Make a plan, but don’t track it – Use Microsoft Project CSC 444 F'07 Lecture 7 7

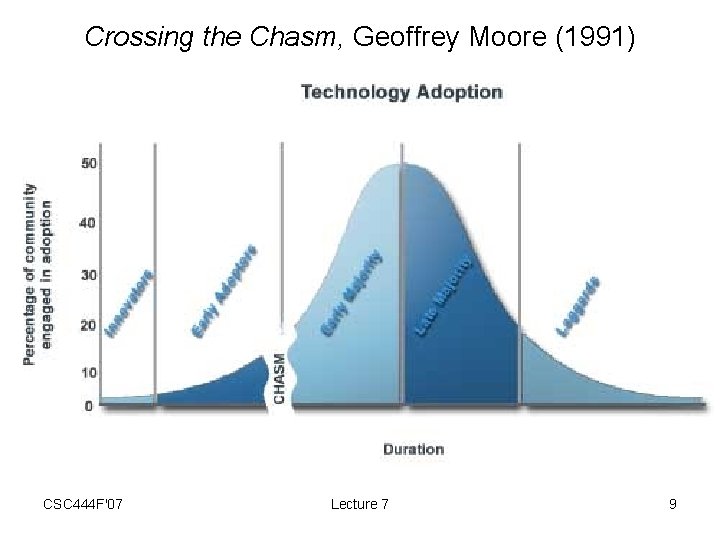
Why Plan? • Not always a good thing – If no expected date – If no other expectations (e. g. , expected functionality) – Planning can only slow you down • Required when – External pressures come to bear on release dates • Usually only happens a bit later in a software company’s business evolution – Not right at the start – Necessary for “crossing the chasm” CSC 444 F'07 Lecture 7 8

Crossing the Chasm, Geoffrey Moore (1991) CSC 444 F'07 Lecture 7 9

Gantt Charts Considered Harmful CSC 444 F'07 Lecture 7 10

Planning Essentials • What are we building? • By when will it be ready? • How many people do we have? Answer these and nothing more: not “who will be doing what? ” nor “what are the detailed tasks required? ” nor “in what order must the tasks be performed? ” CSC 444 F'07 Lecture 7 11

Implementation Plans • Once planning is complete can then transform into a detailed plan – E. g. , Microsoft Project • Detailed plan should not contradict the release plan • Not all of the project needs details beyond – Who do we assign it to – But some parts do • These plans may not be necessary – If no great inter-dependencies that can’t be worked out as you go • They hinder change as they are so cumbersome to change CSC 444 F'07 Lecture 7 12

Of Mice and Men • The essence of planning is uncertainty – Plans never “go according to plan” – Must embrace change, not close our eyes to it • Therefore: – – Must track the plan always Must react quickly to adverse situations Must embrace changes in direction Must re-plan quickly CSC 444 F'07 Lecture 7 13

Internal Changes • Estimation errors – Initial estimates contain a significant (one-sided) margin of error. – As plan progresses, variance in estimates lower • Developer-power leaving the project – – – – Illness Parental leave Resignations Budget cuts Unexpected vacation plans Unexpectedly low work hours Unexpectedly low productivity CSC 444 F'07 Lecture 7 14

External Changes • New (big) customer desiring new functionality • Competitor release a product • Collaboration opportunities • Acquisitions and mergers • Sudden changes in customer needs – E. g. , regulatory changes affecting them CSC 444 F'07 Lecture 7 15

The Difficult Question • What are we building? – – May be hard for 1 st release Subsequent releases will have a big wish list Pick the best looking ones, most demanded ones Marketing product management decision • What will make us the most sales? • By when will it be ready? – Too soon: • Customers won’t be ready for a new release – Won’t want to install – Won’t want to learn – Won’t want to pay for it – Too late • Customers will forget about you • Competitors will pass you • Foregone revenues • How many developers? – Usually fixed for next release • Difficult question – Can we do all 3 at once? CSC 444 F'07 Lecture 7 16

A Common Happening • Often organizations will answer all three questions, but not address the difficult one. • Development management will want to please their masters, and will tend to agree to too much in a spirit of “gung-ho!” – Some managers firmly believe that over-commitment is the road to productivity. – “It’s a stretch, but we’ll pull it off” • Coders will say “it can’t be done” – but “that’s all they ever say”. • Massive sate of denial will set in. – Everybody will hope for a miracle • Nobody will accept any blame – – – Development management: we told you it would be a stretch Coders: we said it could never be done Marketing: you should have said something earlier CEO: you all told me it was going fine Yourdon’s “Death March”. CSC 444 F'07 Lecture 7 17

The Solution: Good Planning! • Does not need to happen this way. • But need courage and conviction. • Need common sense: – Is it even feasible to do what’s asked by the date required? – Don’t give an off-the-cuff answer • Even if it is obviously impossible – Put together a plan and demonstrate the facts. CSC 444 F'07 Lecture 7 18

Release Planning Review The Product Lifecycle CSC 444 F'07 Lecture 7 19

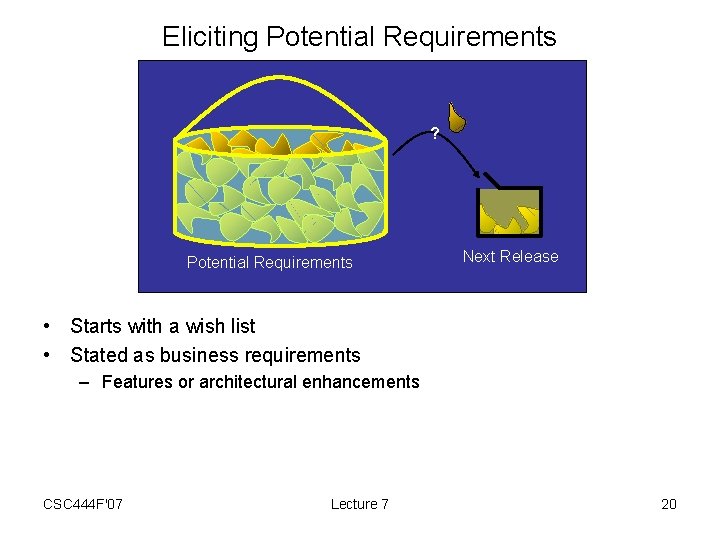
Eliciting Potential Requirements ? Potential Requirements Next Release • Starts with a wish list • Stated as business requirements – Features or architectural enhancements CSC 444 F'07 Lecture 7 20

A Simple Release Plan Dates: Coding phase: Jul. 1—Oct. 1 Beta availability: Nov. 1 General availability: Dec. 1 Capacity: CSC 444 F'07 Fred Lorna … Bill total days available 31 ecd 33 ecd … 21 ecd 317 ecd Requirement: AR report Dialog re-design … Thread support total days required 14 ecd 22 ecd … 87 ecd 317 ecd Status: 317 effective coder-days 0 effective coder days Capacity: Requirement: Delta: Lecture 7 21

Sizing the Available Resources • Who can work on the next release? – Must have skills and familiarity to contribute • For how long? – Must count workdays in the coding phase – Each resource available all that time? – Subtract estimated vacation • How dedicated to the next release – Work factor = w – Converts 8 -hour (nominal, arbitrary) days to time available to code and unit test during the coding phase – E. g. w=0. 6 means can dedicate 0. 6 x 8 = 4. 8 hours/workday – Accounts for • Other tasks, sickdays, meetings, weekends, . . . – Range is 0. . 9, usually 0. 6 or so CSC 444 F'07 Lecture 7 22

Sizing Potential Requirements • Cost / Benefit analysis – Cost: financial + opportunity = person days • Sizing in ECDs – Inherent size of the work item – Who will work on it – The productivity of that person on that work item • Ensure units are well-understood (more later) CSC 444 F'07 Lecture 7 23

The Capacity Constraint • After all is done in a release Actual Resource Used == Sum of Actual Times for Features • This is always true. It is a constraint. • In planning, knowing that this must work out at the end, can estimate both sides and force the estimates to be equal Resource Estimate == Sum of Feature Estimates CSC 444 F'07 Lecture 7 24

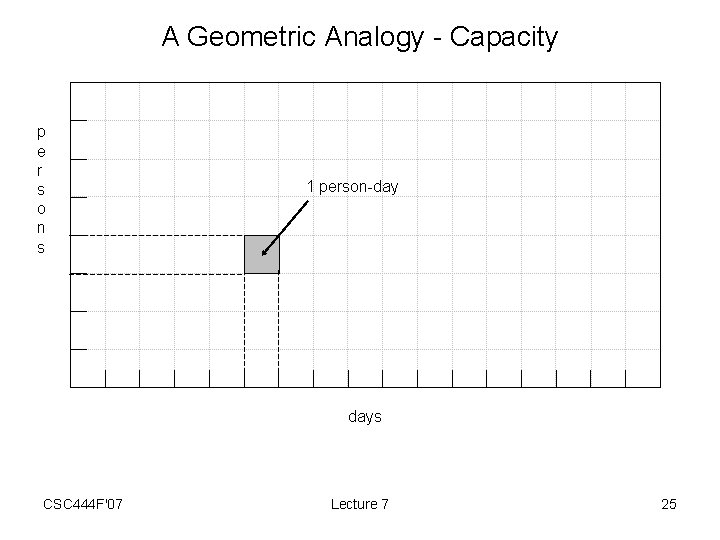
A Geometric Analogy - Capacity p e r s o n s 1 person-day days CSC 444 F'07 Lecture 7 25

A Geometric Analogy - Requirement CSC 444 F'07 Lecture 7 26

A Geometric Analogy - Capacity Constraint It Must All Fit! CSC 444 F'07 Lecture 7 27

Release Planning • What to build • By when to build it • Using how many people F T N F Nx. T • Need to build an initial plan that respects the capacity constraint • Need to continuously update the plan to maintain its adherence to the capacity constraint. CSC 444 F'07 Lecture 7 28

Most Common Problem • Comes from either – not knowing – knowing but hoping for the best (Yourdon Death March) (can happen initially or as we go) CSC 444 F'07 Lecture 7 29

Dealing with Issues as they Arise Developer leaves the team Add time Cut features Both CSC 444 F'07 Lecture 7 30

Other Happenings CSC 444 F'07 Lecture 7 31

Organizational Issues • Management must appreciate that software development carries with it certain inherent risks. • The business of a software organization is to manage and adapt as possibilities continuously become reality. • Ranting and raving is unproductive • With good data, good managers will make good decisions. CSC 444 F'07 Lecture 7 32

The Quantitative Capacity Constraint • Post-Facto, the following relationship must hold. – But, it requires careful definition. We define carefully so that we know what it is we are trying to estimate, and how to compare actuals against estimates for post-mortem. CSC 444 F'07 Lecture 7 33

Number of Workdays: T • The number of full-equivalent working days fork to dcut. • Subtracts – Weekends – Statutory holidays – “Company Days” • Subtracts anything we know in advance that nobody is expected to work. CSC 444 F'07 Lecture 7 34

Developer Power: N • The average number of dedicated developers per workday working during the T-day period. • Dedicated Developer? CSC 444 F'07 Lecture 7 35

Work Time & Dedicated Time • Work Time or Body Time – Defined as 8 hours per workday • Excludes weekends, stat. holidays, vacation entitlement. • E. g. , 9 -to-6 with 1 hour for lunch. • Dedicated Time – Uninterrupted hour equivalents. – Time dedicated to adding new features to the release. • Uninterrupted Time – 4 hrs with 30 min. of constant interruptions • Not 3. 5 hrs of dedicated uninterrupted time – more like 2 – 2 hrs with NO interruptions at all CSC 444 F'07 Lecture 7 36

Examples of Dedicated Losses • Maintenance (tracking down and fixing defects) on previous releases • Other simultaneous projects • Team-leader duties (& helping others) • Meetings • Training • Unexpected, non-made-up days off (e. g. , sick days) • Sales/marketing support • Loss of flow due to interruptions CSC 444 F'07 Lecture 7 37

Measuring N • Assume each developer understands the concept of a dedicated uninterrupted hour. • Get each of the n developers to record how many dedicated uninterrupted hours they spent in total during the coding phase. • hi is what’s in the time tracking system for the ith developer. CSC 444 F'07 Lecture 7 38

Attributing N • di is the number of days available during the coding phase • vi is the number of vacation days they took during the coding phase • hi is as before Substitute to get back to: CSC 444 F'07 Lecture 7 39

Example • Bob called in sick for 2 days: accounted for in h • Bob took an afternoon off, but worked on the weekend to make up for it: accounted for in h CSC 444 F'07 Lecture 7 40

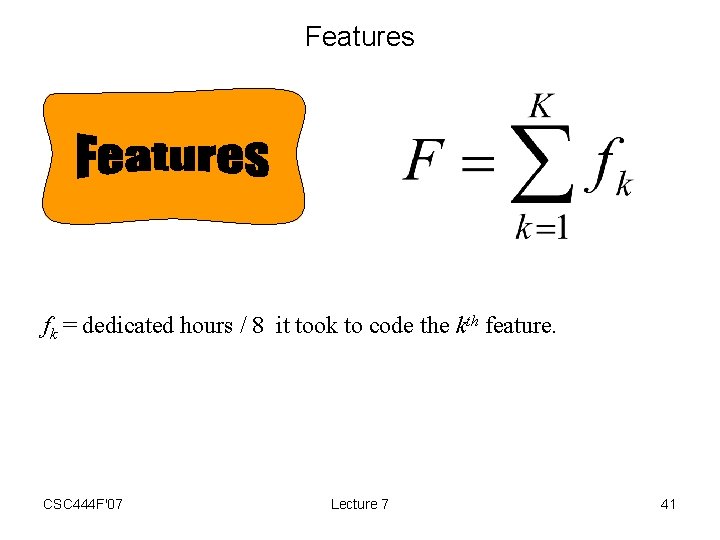
Features fk = dedicated hours / 8 it took to code the kth feature. CSC 444 F'07 Lecture 7 41

Post-Mortem • Imagine a time-tracking system that could track – hi, k, d • dedicated (uninterrupted) hours spent – by the ith developer – on the dth day – doing coding work on the kth feature • each such quantum would appear on both sides of F= N x T constraining them to be equal. • See section 5. 10 in book for proof. CSC 444 F'07 Lecture 7 42

Example Release Plan • Sample Deterministic Release Plan CSC 444 F'07 Lecture 7 43

The Stochastic Capacity Constraint CSC 444 F'07 Lecture 7 44

Estimates • Estimates are never 100% certain • E. g, if we estimate a feature at 20 ECD’s – Not saying will be done in 20 ECDs – But then what are we saying? • Are we confident in it? • Is it optimistic? • Is it pessimistic? • A quantity whose value depends upon unknowns (or upon random chance) is called a stochastic variable • Release planning contains many such stochastic variables. CSC 444 F'07 Lecture 7 45

Confidence Intervals • Say we toss a fair coin 5000 times – We expect it to come up heads ½ the time – 2500 times or so – Exactly 2500? • Chance is only 1. 1% – ≤ 2500? • Chance is 50% • If we repeat this experiment over and over again (tossing a coin 5000 times), on average ½ the time it will be more, ½ the time less. – ≤ 2530? • Chance is 80% – ≤ 2550? • Chance is 92% • These (50%, 80%, 92%) are called confidence intervals – With 80% confidence we can say that the number of heads will be less than 2530. CSC 444 F'07 Lecture 7 46

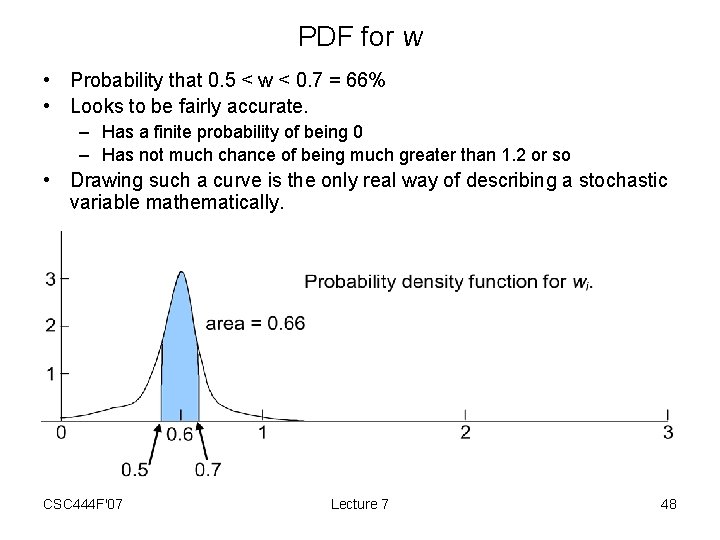
Stochastic Variables • Consider the work factor of a coder, w. – When estimating in advance, w is a stochastic variable. – Stochastic variables are described by statistical distributions – A statistical distribution will tell you: • For any range of w • The probability of w being within that range – Can be described completely with a probability density function. • X-axis: all possible values of the stochastic variable • Y-axis: numbers >= 0 • The probability that the stochastic variables lies between two values a and b is given by the area under the p. d. f. between a and b. CSC 444 F'07 Lecture 7 47

PDF for w • Probability that 0. 5 < w < 0. 7 = 66% • Looks to be fairly accurate. – Has a finite probability of being 0 – Has not much chance of being much greater than 1. 2 or so • Drawing such a curve is the only real way of describing a stochastic variable mathematically. CSC 444 F'07 Lecture 7 48

Parameterized Distributions • “So, Bill, here’s a piece of paper, could you please draw me a p. d. f. for your work factor? ” – Nobody knows the distribution to this level of accuracy – Very hard to work with mathematically • Usual method is to make an assumption about the overall shape of the curve, choosing from a few set shapes that are easy to work with mathematically. • Then ask Bill for a few parameters that we can use to fit the curve. • Because we are not so sure on our estimates anyways, the relative inaccuracy of choosing from one of a set of mathematically tractable p. d. f. ’s is small compared to the other estimation errors. CSC 444 F'07 Lecture 7 49

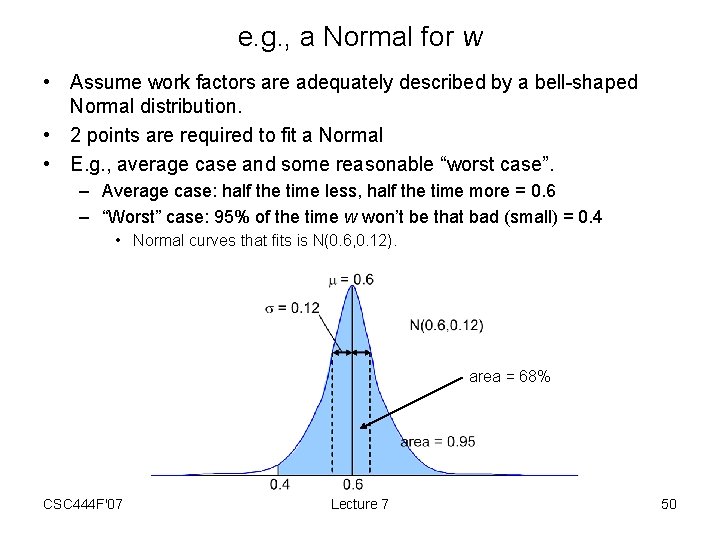
e. g. , a Normal for w • Assume work factors are adequately described by a bell-shaped Normal distribution. • 2 points are required to fit a Normal • E. g. , average case and some reasonable “worst case”. – Average case: half the time less, half the time more = 0. 6 – “Worst” case: 95% of the time w won’t be that bad (small) = 0. 4 • Normal curves that fits is N(0. 6, 0. 12). area = 68% CSC 444 F'07 Lecture 7 50

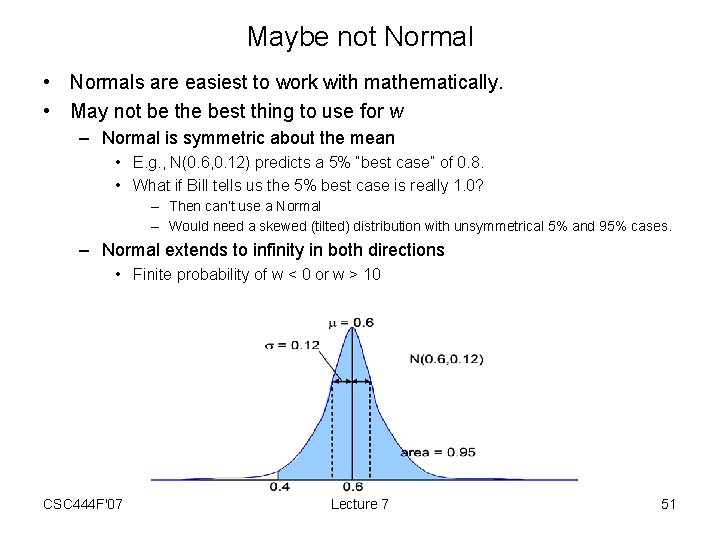
Maybe not Normal • Normals are easiest to work with mathematically. • May not be the best thing to use for w – Normal is symmetric about the mean • E. g. , N(0. 6, 0. 12) predicts a 5% “best case” of 0. 8. • What if Bill tells us the 5% best case is really 1. 0? – Then can’t use a Normal – Would need a skewed (tilted) distribution with unsymmetrical 5% and 95% cases. – Normal extends to infinity in both directions • Finite probability of w < 0 or w > 10 CSC 444 F'07 Lecture 7 51

Estimates • Most define our quantities very precisely • E. g. , for a feature estimate of 1 week – Post-Facto • What are the units? • 40 hours? Longer? Shorter? Dedicated? Disrupted? One person or two? . . . • Dealt with this last lecture in great detail – Stochastic • • 1 week best case? 1 week worst case? 1 week average case? Need a p. d. f • Depending upon these concerns, my “ 1 week” maybe somebody else’s 4 weeks. – Very significant issue in practice CSC 444 F'07 Lecture 7 52

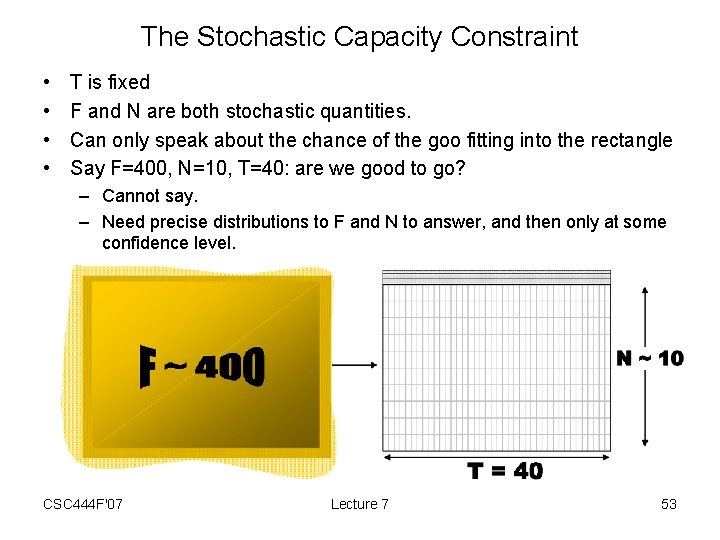
The Stochastic Capacity Constraint • • T is fixed F and N are both stochastic quantities. Can only speak about the chance of the goo fitting into the rectangle Say F=400, N=10, T=40: are we good to go? – Cannot say. – Need precise distributions to F and N to answer, and then only at some confidence level. CSC 444 F'07 Lecture 7 53

Summing Distributions • • F and N are sums and products over many contributing stochastic variables. E. g. – F = f 1 + f 2 – If f 1 and f 2 have associated statistical distributions, what is the statistical distribution of F? – In general, no answer. – Special case: f 1 and f 2 are both Normal • Then F will be Normal as well. • Mean of F will be the sums of the means of f 1 and f 2 • Standard deviation of F will be the square root of the sums of the squares of the standard deviations of f 1 and f 2. – How about f 1 * f 2? • Figet about it! Huge formula, result is not a Normal distribution – One needs statistical simulation software tools to do arithmetic on stochastic variables. CSC 444 F'07 Lecture 7 54

Law of Large Numbers • If we sum lots and lots of stochastic variables, the sum will approach a Normal distribution. • Therefore something like F is going to be pretty close to Normal. – E. g. , 400 features summed • N will also be, but a bit less so – E. g. , 10 w’s summed CSC 444 F'07 Lecture 7 55

Delta Statistic • D(T) = N T F • If we have Normal approximations for N and F, can compute the Normal curve for D as a function of various T’s. • We can then choose a T that leads to a D we can live with. • Interested in Probability [ D(T) 0 ] • The probability that all features will be finished by dcut. • In choosing T will want to choose a confidence interval the company can live with, e. g. , 80%. • Then will pick a T such that D(T) 0 80% of the time. CSC 444 F'07 Lecture 7 56

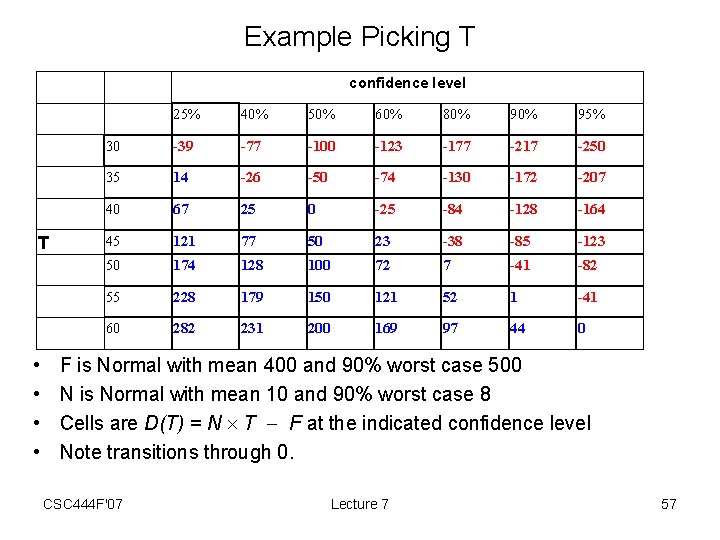
Example Picking T confidence level T • • 25% 40% 50% 60% 80% 95% 30 -39 -77 -100 -123 -177 -217 -250 35 14 -26 -50 -74 -130 -172 -207 40 67 25 0 -25 -84 -128 -164 45 121 77 50 23 -38 -85 -123 50 174 128 100 72 7 -41 -82 55 228 179 150 121 52 1 -41 60 282 231 200 169 97 44 0 F is Normal with mean 400 and 90% worst case 500 N is Normal with mean 10 and 90% worst case 8 Cells are D(T) = N T F at the indicated confidence level Note transitions through 0. CSC 444 F'07 Lecture 7 57

Choices for T • To be 95% certain of hitting the dates, choose T = 60 workdays • Or. . . If we plan to take 40 workdays, only 5% of the time will be late by more than 20 workdays • To be 80% sure, T = 49 • To gamble, for a 25% fighting chance, make T = 33. CSC 444 F'07 Lecture 7 58

Shortcut • Ask for 80% worst case estimates for everything. • If F = Nx. T using the 80% worst case values, then there is an 80% chance of making the release. • The Deterministic Release Plan is based on this approach. • If you also ask for mean cases for everything, can then fit a Normal distribution for D(T) and can predict the approximate probability of slipping. CSC 444 F'07 Lecture 7 59

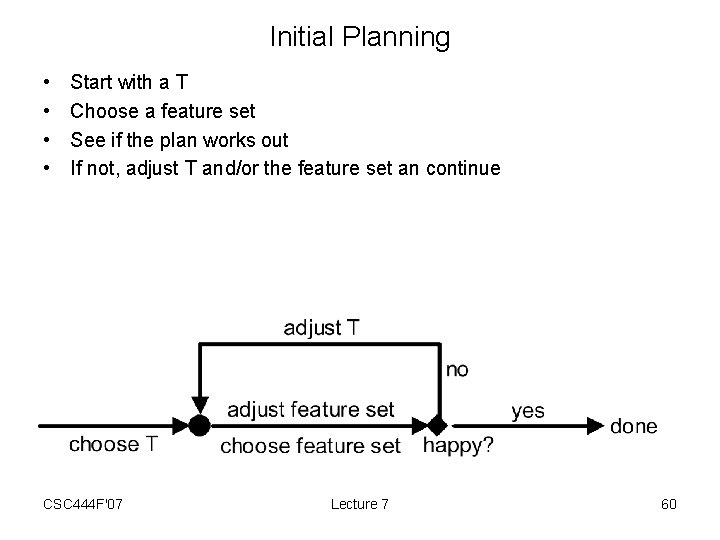
Initial Planning • • Start with a T Choose a feature set See if the plan works out If not, adjust T and/or the feature set an continue CSC 444 F'07 Lecture 7 60

Adjusting the Release Plan • Count on the w estimated to be too high and feature estimates to be too low. • Re-adjust as new data comes in. • Can “pad the plan” by choosing a 95% T. – Will make it with a high degree of confidence – May run out of work – May gold plate features • Better to have an A-list and a B-list – Choose one T such that, e. g. , • Have 95% confidence of making the A list • Have 40% confidence of making the A+B list. CSC 444 F'07 Lecture 7 61

Risk Tolerance • Say a plan is at 60% • Developer may say: – Chances are poor: 60% at best • An entrepreneurial CEO will say – Looking great! At least a 60% chance of making it. • Should have an explicit discussion of risk tolerance CSC 444 F'07 Lecture 7 62

Loading the Dice • Can manage to affect the outcome. • Like a football game: – Odds may be 3 -to-1 against a team winning – But by making a special effort, the team may still win • In release planning – Base the odds on history – But as a manager, don’t ever accept that history is as good as you can do! • E. g. , introduce a new practice that will boost productivity – – Estimate will increase productivity by 20% Don’t plan for that! Plan for what was achieved historically. Manage to get that 20% and change history for next time around. CSC 444 F'07 Lecture 7 63

Example Stochastic Release Plan • Sample Stochastic Release Plan CSC 444 F'07 Lecture 7 64