CPU Performance Evaluation Cycles Per Instruction CPI Most


























- Slides: 45

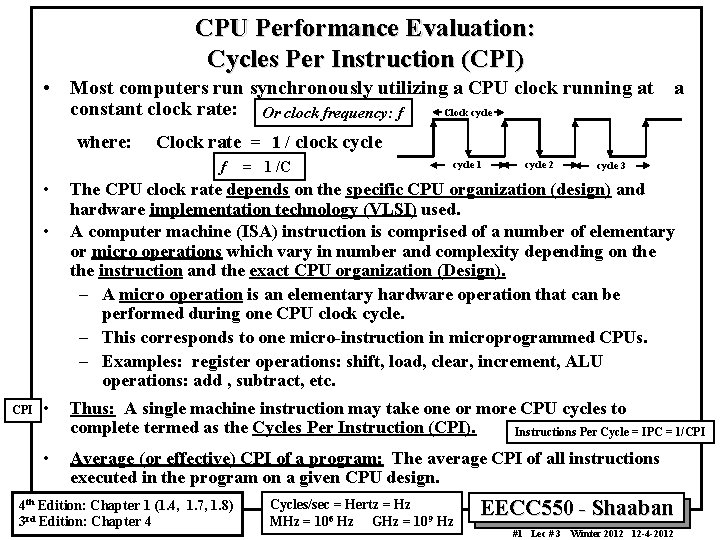
CPU Performance Evaluation: Cycles Per Instruction (CPI) • Most computers run synchronously utilizing a CPU clock running at a constant clock rate: Or clock frequency: f Clock cycle where: Clock rate = 1 / clock cycle f • • CPI = 1 /C cycle 1 cycle 2 cycle 3 The CPU clock rate depends on the specific CPU organization (design) and hardware implementation technology (VLSI) used. A computer machine (ISA) instruction is comprised of a number of elementary or micro operations which vary in number and complexity depending on the instruction and the exact CPU organization (Design). – A micro operation is an elementary hardware operation that can be performed during one CPU clock cycle. – This corresponds to one micro-instruction in microprogrammed CPUs. – Examples: register operations: shift, load, clear, increment, ALU operations: add , subtract, etc. • Thus: A single machine instruction may take one or more CPU cycles to complete termed as the Cycles Per Instruction (CPI). Instructions Per Cycle = IPC = 1/CPI • Average (or effective) CPI of a program: The average CPI of all instructions executed in the program on a given CPU design. 4 th Edition: Chapter 1 (1. 4, 1. 7, 1. 8) 3 rd Edition: Chapter 4 Cycles/sec = Hertz = Hz MHz = 106 Hz GHz = 109 Hz EECC 550 - Shaaban #1 Lec # 3 Winter 2012 12 -4 -2012

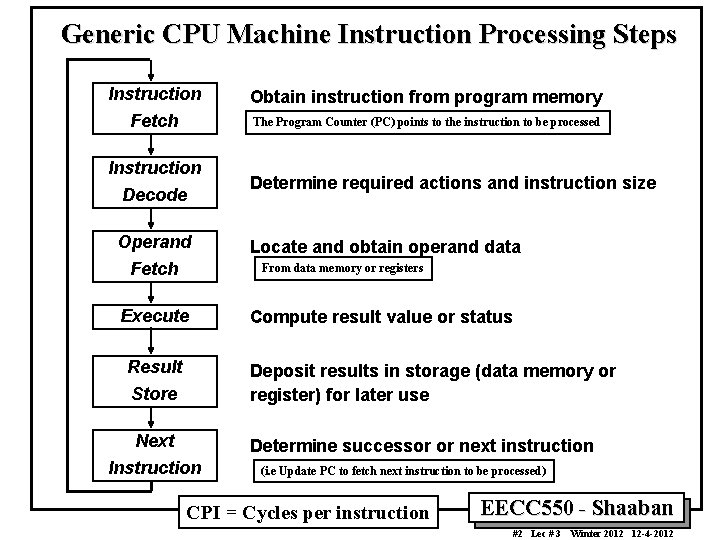
Generic CPU Machine Instruction Processing Steps Instruction Obtain instruction from program memory Fetch The Program Counter (PC) points to the instruction to be processed Instruction Decode Operand Fetch Determine required actions and instruction size Locate and obtain operand data From data memory or registers Execute Result Compute result value or status Store Deposit results in storage (data memory or register) for later use Next Determine successor or next instruction Instruction (i. e Update PC to fetch next instruction to be processed) CPI = Cycles per instruction EECC 550 - Shaaban #2 Lec # 3 Winter 2012 12 -4 -2012

Computer Performance Measures: Program Execution Time • For a specific program compiled to run on a specific machine (CPU) “A”, has the following parameters: – The total executed instruction count of the program. I – The average number of cycles per instruction (average CPI). CPI – Clock cycle of machine “A” C Or effective CPI • How can one measure the performance of this machine (CPU) running this program? – Intuitively the machine (or CPU) is said to be faster or has better performance running this program if the total execution time is shorter. – Thus the inverse of the total measured program execution time is a possible performance measure or metric: Seconds/program Programs/second Performance. A = 1 / Execution Time. A How to compare performance of different machines? What factors affect performance? How to improve performance? EECC 550 - Shaaban #3 Lec # 3 Winter 2012 12 -4 -2012

Comparing Computer Performance Using Execution Time • To compare the performance of two machines (or CPUs) “A”, “B” running a given specific program: Performance. A = 1 / Execution Time. A Performance. B = 1 / Execution Time. B • Machine A is n times faster than machine B means (or slower? if n < 1) : Speedup = n = • Performance. A Performance. B Example: For a given program: Execution time on machine A: Execution time on machine B: Speedup= Performance. A / Performance. B = Execution Time. B Execution Time. A (i. e Speedup is ratio of performance, no units) Execution. A = 1 second Execution. B = 10 seconds = Execution Time. B / Execution Time. A = 10 / 1 = 10 The performance of machine A is 10 times the performance of machine B when running this program, or: Machine A is said to be 10 times faster than machine B when running this program. The two CPUs may target different ISAs provided the program is written in a high level language (HLL) EECC 550 - Shaaban #4 Lec # 3 Winter 2012 12 -4 -2012

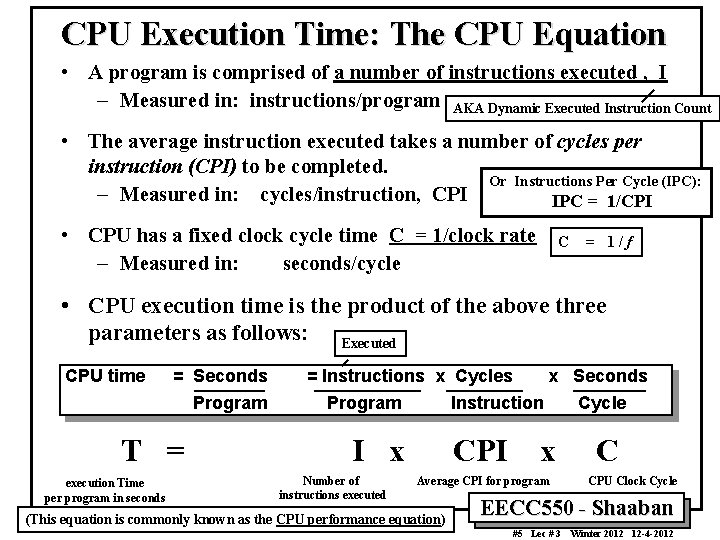
CPU Execution Time: The CPU Equation • A program is comprised of a number of instructions executed , I – Measured in: instructions/program AKA Dynamic Executed Instruction Count • The average instruction executed takes a number of cycles per instruction (CPI) to be completed. Or Instructions Per Cycle (IPC): – Measured in: cycles/instruction, CPI IPC = 1/CPI • CPU has a fixed clock cycle time C = 1/clock rate – Measured in: seconds/cycle C = 1/f • CPU execution time is the product of the above three parameters as follows: Executed CPU time = Seconds Program T = execution Time per program in seconds = Instructions x Cycles Program Instruction I x Number of instructions executed x Seconds CPI x Average CPI for program (This equation is commonly known as the CPU performance equation) Cycle C CPU Clock Cycle EECC 550 - Shaaban #5 Lec # 3 Winter 2012 12 -4 -2012

CPU Average CPI/Execution Time For a given program executed on a given machine (CPU): CPI = Total program execution cycles / Instructions count Executed (I) (i. e average or effective CPI) ® CPU clock cycles = Instruction count x CPI CPU execution time = T (executed, I) = CPU clock cycles x Clock cycle = Instruction count x CPI x Clock cycle = I x CPI x C execution Time per program in seconds Number of instructions executed Average or effective CPI for program CPU Clock Cycle (This equation is commonly known as the CPU performance equation) CPI = Cycles Per Instruction EECC 550 - Shaaban #6 Lec # 3 Winter 2012 12 -4 -2012

CPU Execution Time: Example • A Program is running on a specific machine (CPU) with I the following parameters: – Total executed instruction count: 10, 000 instructions – Average CPI for the program: 2. 5 cycles/instruction. – CPU clock rate: 200 MHz. (clock cycle = C = 5 x 10 -9 seconds) • What is the execution time for this program: CPU time = Seconds Program = Instructions x Cycles Program i. e 5 nanoseconds x Seconds Instruction Cycle CPU time = Instruction count x CPI x Clock cycle = 10, 000 x 2. 5 x 1 / clock rate = 10, 000 x 2. 5 x 5 x 10 -9 = 0. 125 seconds Nanosecond = nsec =ns = 10 -9 second MHz = 106 Hz T = I x CPI x C EECC 550 - Shaaban #7 Lec # 3 Winter 2012 12 -4 -2012

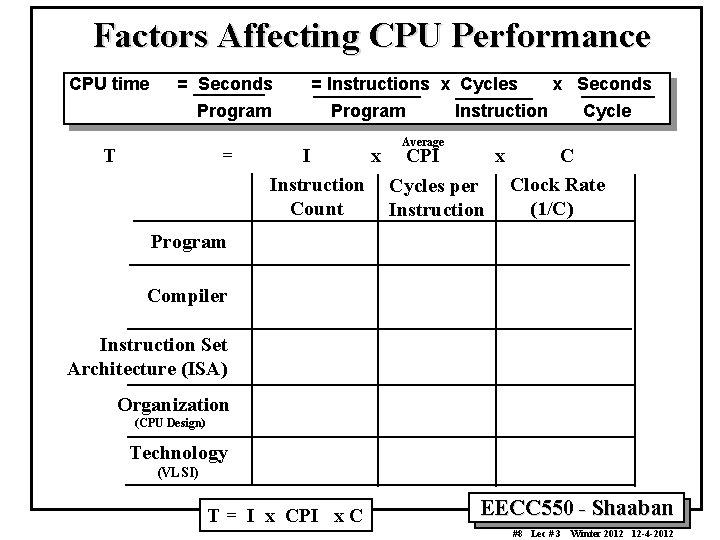
Factors Affecting CPU Performance CPU time = Seconds Program T = = Instructions x Cycles Program x Seconds Instruction Cycle Average I x CPI x C Instruction Cycles per Clock Rate Count (1/C) Instruction Program Compiler Instruction Set Architecture (ISA) Organization (CPU Design) Technology (VLSI) T = I x CPI x C EECC 550 - Shaaban #8 Lec # 3 Winter 2012 12 -4 -2012

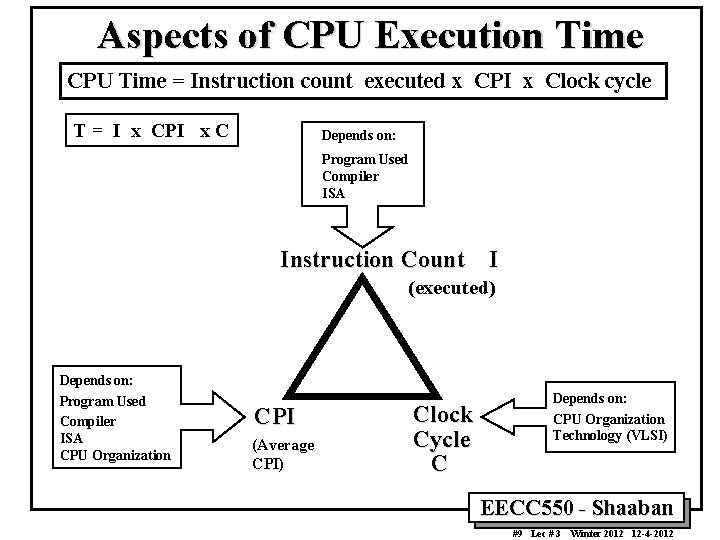
Aspects of CPU Execution Time CPU Time = Instruction count executed x CPI x Clock cycle T = I x CPI x C Depends on: Program Used Compiler ISA Instruction Count I (executed) Depends on: Program Used Compiler ISA CPU Organization CPI (Average CPI) Clock Cycle C Depends on: CPU Organization Technology (VLSI) EECC 550 - Shaaban #9 Lec # 3 Winter 2012 12 -4 -2012

Performance Comparison: Example • From the previous example: A Program is running on a specific machine (CPU) with the following parameters: – Total executed instruction count, I: 10, 000 instructions – Average CPI for the program: 2. 5 cycles/instruction. – CPU clock rate: 200 MHz. Thus: C = 1/(200 x 10 )= 5 x 10 seconds • Using the same program with these changes: – A new compiler used: New executed instruction count, I: 9, 500, 000 New CPI: 3. 0 – Faster CPU implementation: New clock rate = 300 MHz Thus: C = 1/(300 x 10 )= 3. 33 x 10 seconds • What is the speedup with the changes? 6 -9 6 Speedup = Old Execution Time = Iold x New Execution Time Inew x CPIold x Clock cycleold CPInew x Clock Cyclenew -9 Speedup = (10, 000 x 2. 5 x 5 x 10 -9) / (9, 500, 000 x 3. 33 x 10 -9 ) =. 125 /. 095 = 1. 32 or 32 % faster after changes. Clock Cycle = C = 1/ Clock Rate T = I x CPI x C EECC 550 - Shaaban #10 Lec # 3 Winter 2012 12 -4 -2012

Instruction Types & CPI • Given a program with n types or classes of instructions executed on given CPU with the following characteristics: a e. g ALU, Branch etc. Ci = Count of instructions of typei executed CPIi = Cycles per instruction for typei Then: i = 1, 2, …. n Depends on CPU Design CPI = CPU Clock Cycles / Instruction Count I i. e average or effective CPI Where: Executed Instruction Count I = S Ci T = I x CPI x C EECC 550 - Shaaban #11 Lec # 3 Winter 2012 12 -4 -2012

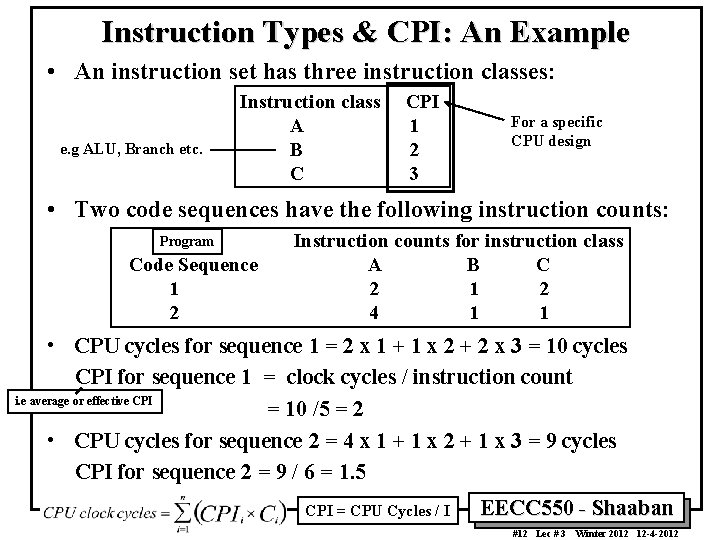
Instruction Types & CPI: An Example • An instruction set has three instruction classes: e. g ALU, Branch etc. Instruction class A B C CPI 1 2 3 For a specific CPU design • Two code sequences have the following instruction counts: Program Code Sequence 1 2 Instruction counts for instruction class A B C 2 1 2 4 1 1 • CPU cycles for sequence 1 = 2 x 1 + 1 x 2 + 2 x 3 = 10 cycles CPI for sequence 1 = clock cycles / instruction count i. e average or effective CPI = 10 /5 = 2 • CPU cycles for sequence 2 = 4 x 1 + 1 x 2 + 1 x 3 = 9 cycles CPI for sequence 2 = 9 / 6 = 1. 5 CPI = CPU Cycles / I EECC 550 - Shaaban #12 Lec # 3 Winter 2012 12 -4 -2012

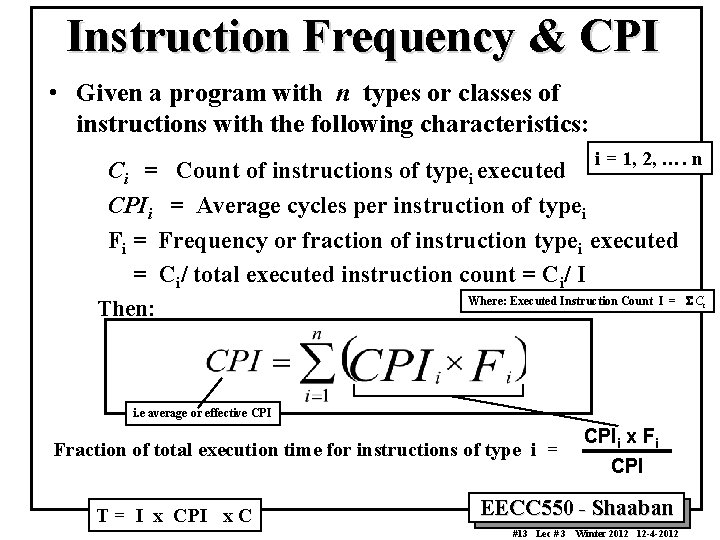
Instruction Frequency & CPI • Given a program with n types or classes of instructions with the following characteristics: i = 1, 2, …. n Ci = Count of instructions of typei executed CPIi = Average cycles per instruction of typei Fi = Frequency or fraction of instruction typei executed = Ci/ total executed instruction count = Ci/ I Where: Executed Instruction Count I = S C Then: i. e average or effective CPI Fraction of total execution time for instructions of type i = T = I x CPI x C CPIi x Fi CPI EECC 550 - Shaaban #13 Lec # 3 Winter 2012 12 -4 -2012 i

Instruction Type Frequency & CPI: A RISC Example CPIi x Fi Program Profile or Executed Instructions Mix Given Base Machine (Reg / Reg) Op Freq, Fi CPIi ALU 50% 1 Load 20% 5 Store 10% 3 Branch 20% 2 Typical Mix CPI Depends on CPU Design CPIi x Fi. 5 1. 0. 3. 4 % Time 23% =. 5/2. 2 45% = 1/2. 2 14% =. 3/2. 2 18% =. 4/2. 2 Sum = 2. 2 i. e average or effective CPI =. 5 x 1 +. 2 x 5 +. 1 x 3 +. 2 x 2 = 2. 2 =. 5 + 1 +. 3 +. 4 T = I x CPI x C EECC 550 - Shaaban #14 Lec # 3 Winter 2012 12 -4 -2012

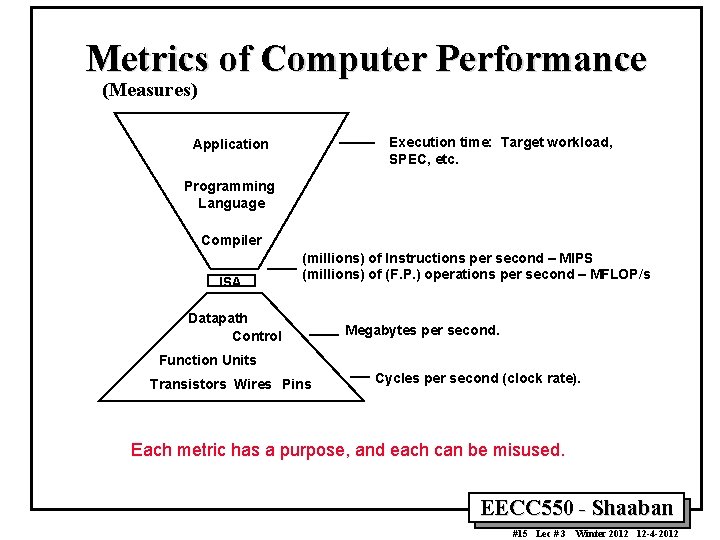
Metrics of Computer Performance (Measures) Execution time: Target workload, SPEC, etc. Application Programming Language Compiler ISA (millions) of Instructions per second – MIPS (millions) of (F. P. ) operations per second – MFLOP/s Datapath Control Megabytes per second. Function Units Transistors Wires Pins Cycles per second (clock rate). Each metric has a purpose, and each can be misused. EECC 550 - Shaaban #15 Lec # 3 Winter 2012 12 -4 -2012

Choosing Programs To Evaluate Performance Levels of programs or benchmarks that could be used to evaluate performance: – Actual Target Workload: Full applications that run on the target machine. – Real Full Program-based Benchmarks: • Select a specific mix or suite of programs that are typical of targeted applications or workload (e. g SPEC 95, SPEC CPU 2000). – Small “Kernel” Benchmarks: Also called synthetic benchmarks • Key computationally-intensive pieces extracted from real programs. – Examples: Matrix factorization, FFT, tree search, etc. • Best used to test specific aspects of the machine. – Microbenchmarks: • Small, specially written programs to isolate a specific aspect of performance characteristics: Processing: integer, floating point, local memory, input/output, etc. EECC 550 - Shaaban #16 Lec # 3 Winter 2012 12 -4 -2012

Pros Types of Benchmarks • Representative • Portable. • Widely used. • Measurements useful in reality. Actual Target Workload Full Application Benchmarks • Easy to run, early in the design cycle. • Identify peak performance and potential bottlenecks. Small “Kernel” Benchmarks Microbenchmarks Cons • Very specific. • Non-portable. • Complex: Difficult to run, or measure. • Less representative than actual workload. • Easy to “fool” by designing hardware to run them well. • Peak performance results may be a long way from real application performance EECC 550 - Shaaban #17 Lec # 3 Winter 2012 12 -4 -2012

SPEC: System Performance Evaluation Corporation The most popular and industry-standard set of CPU benchmarks. • SPECmarks, 1989: Programs application domain: Engineering and scientific computation – 10 programs yielding a single number (“SPECmarks”). • SPEC 92, 1992: – SPECInt 92 (6 integer programs) and SPECfp 92 (14 floating point programs). • SPEC 95, 1995: – SPECint 95 (8 integer programs): – – • go, m 88 ksim, gcc, compress, li, ijpeg, perl, vortex SPECfp 95 (10 floating-point intensive programs): • tomcatv, swim, su 2 cor, hydro 2 d, mgrid, applu, turb 3 d, apsi, fppp, wave 5 Performance relative to a Sun Super. Spark I (50 MHz) which is given a score of SPECint 95 = SPECfp 95 = 1 • SPEC CPU 2000, 1999: – CINT 2000 (11 integer programs). CFP 2000 (14 floating-point intensive programs) – Performance relative to a Sun Ultra 5_10 (300 MHz) which is given a score of SPECint 2000 = SPECfp 2000 = 100 • SPEC CPU 2006, 2006: – CINT 2006 (12 integer programs). CFP 2006 (17 floating-point intensive programs) – Performance relative to a Sun Ultra Enterprise 2 workstation with a 296 -MHz Ultra. SPARC II processor which is given a score of SPECint 2006 = SPECfp 2006 = 1 All based on execution time and give speedup over a reference CPU EECC 550 - Shaaban #18 Lec # 3 Winter 2012 12 -4 -2012

SPEC 95 Programs application domain: Engineering and scientific computation Integer Floating Point Resulting Performance relative to a Sun Super. Spark I (50 MHz) which is given a score of SPECint 95 = SPECfp 95 = 1 EECC 550 - Shaaban #19 Lec # 3 Winter 2012 12 -4 -2012

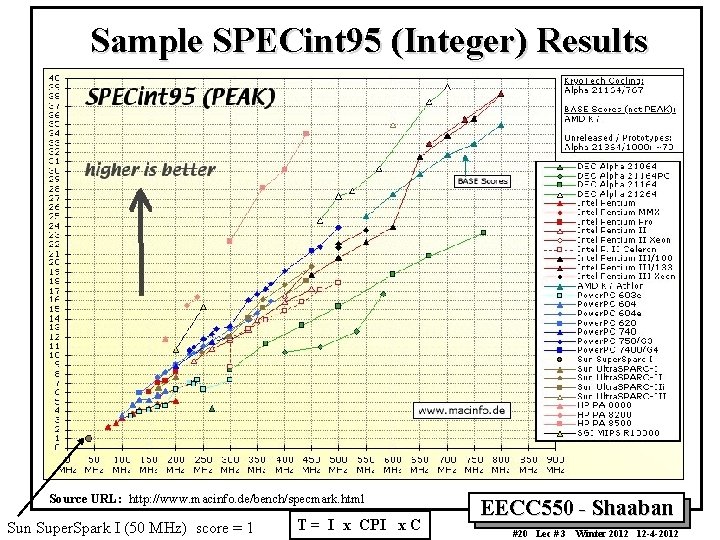
Sample SPECint 95 (Integer) Results Source URL: http: //www. macinfo. de/bench/specmark. html Sun Super. Spark I (50 MHz) score = 1 T = I x CPI x C EECC 550 - Shaaban #20 Lec # 3 Winter 2012 12 -4 -2012

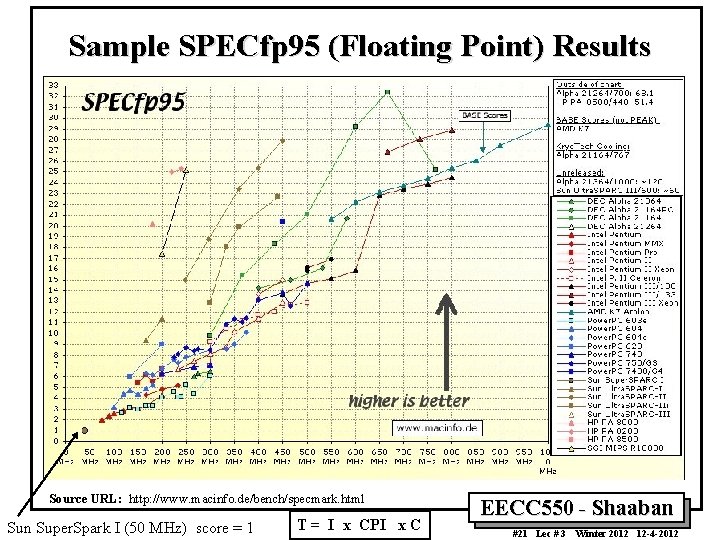
Sample SPECfp 95 (Floating Point) Results Source URL: http: //www. macinfo. de/bench/specmark. html Sun Super. Spark I (50 MHz) score = 1 T = I x CPI x C EECC 550 - Shaaban #21 Lec # 3 Winter 2012 12 -4 -2012

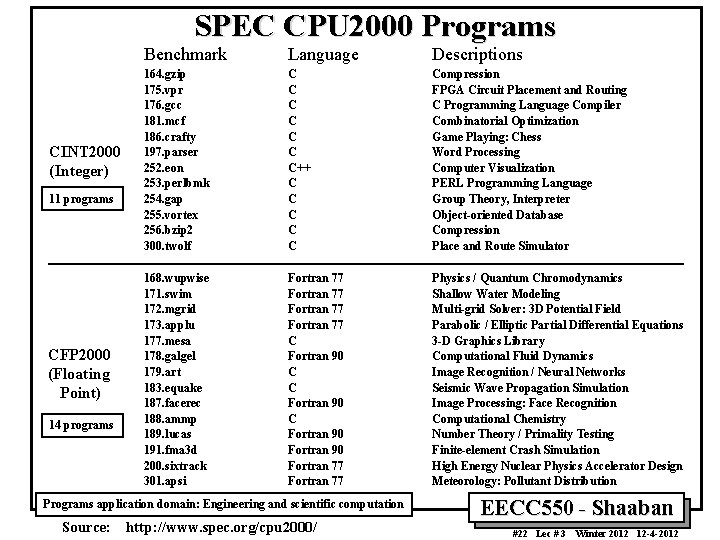
SPEC CPU 2000 Programs CINT 2000 (Integer) 11 programs CFP 2000 (Floating Point) 14 programs Benchmark Language Descriptions 164. gzip 175. vpr 176. gcc 181. mcf 186. crafty 197. parser 252. eon 253. perlbmk 254. gap 255. vortex 256. bzip 2 300. twolf C C C C++ C C Compression FPGA Circuit Placement and Routing C Programming Language Compiler Combinatorial Optimization Game Playing: Chess Word Processing Computer Visualization PERL Programming Language Group Theory, Interpreter Object-oriented Database Compression Place and Route Simulator 168. wupwise 171. swim 172. mgrid 173. applu 177. mesa 178. galgel 179. art 183. equake 187. facerec 188. ammp 189. lucas 191. fma 3 d 200. sixtrack 301. apsi Fortran 77 C Fortran 90 Fortran 77 Physics / Quantum Chromodynamics Shallow Water Modeling Multi-grid Solver: 3 D Potential Field Parabolic / Elliptic Partial Differential Equations 3 -D Graphics Library Computational Fluid Dynamics Image Recognition / Neural Networks Seismic Wave Propagation Simulation Image Processing: Face Recognition Computational Chemistry Number Theory / Primality Testing Finite-element Crash Simulation High Energy Nuclear Physics Accelerator Design Meteorology: Pollutant Distribution Programs application domain: Engineering and scientific computation Source: http: //www. spec. org/cpu 2000/ EECC 550 - Shaaban #22 Lec # 3 Winter 2012 12 -4 -2012

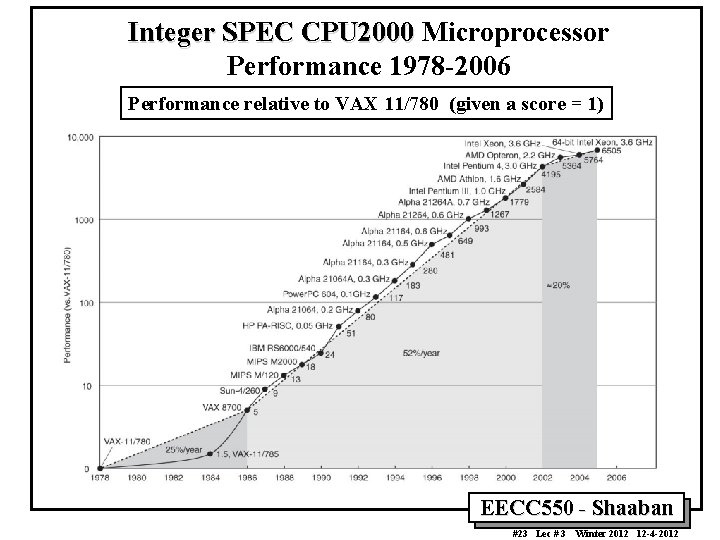
Integer SPEC CPU 2000 Microprocessor Performance 1978 -2006 Performance relative to VAX 11/780 (given a score = 1) EECC 550 - Shaaban #23 Lec # 3 Winter 2012 12 -4 -2012

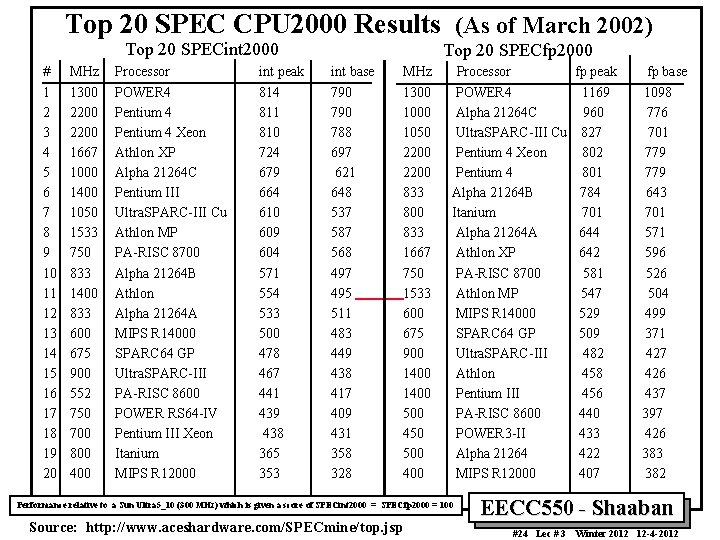
Top 20 SPEC CPU 2000 Results (As of March 2002) Top 20 SPECint 2000 Top 20 SPECfp 2000 # MHz Processor int peak int base MHz 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1300 2200 1667 1000 1400 1050 1533 750 833 1400 833 600 675 900 552 750 700 800 400 POWER 4 Pentium 4 Xeon Athlon XP Alpha 21264 C Pentium III Ultra. SPARC-III Cu Athlon MP PA-RISC 8700 Alpha 21264 B Athlon Alpha 21264 A MIPS R 14000 SPARC 64 GP Ultra. SPARC-III PA-RISC 8600 POWER RS 64 -IV Pentium III Xeon Itanium MIPS R 12000 814 811 810 724 679 664 610 609 604 571 554 533 500 478 467 441 439 438 365 353 790 788 697 621 648 537 587 568 497 495 511 483 449 438 417 409 431 358 328 1300 1050 2200 833 800 833 1667 750 1533 600 675 900 1400 500 450 500 400 Processor POWER 4 Alpha 21264 C Ultra. SPARC-III Cu Pentium 4 Xeon Pentium 4 Alpha 21264 B Itanium Alpha 21264 A Athlon XP PA-RISC 8700 Athlon MP MIPS R 14000 SPARC 64 GP Ultra. SPARC-III Athlon Pentium III PA-RISC 8600 POWER 3 -II Alpha 21264 MIPS R 12000 Performance relative to a Sun Ultra 5_10 (300 MHz) which is given a score of SPECint 2000 = SPECfp 2000 = 100 Source: http: //www. aceshardware. com/SPECmine/top. jsp fp peak 1169 960 827 802 801 784 701 644 642 581 547 529 509 482 458 456 440 433 422 407 fp base 1098 776 701 779 643 701 571 596 526 504 499 371 427 426 437 397 426 383 382 EECC 550 - Shaaban #24 Lec # 3 Winter 2012 12 -4 -2012

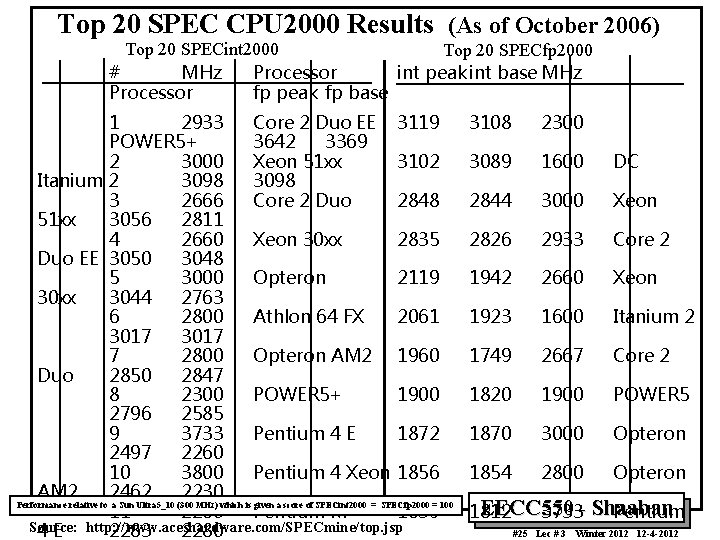
Top 20 SPEC CPU 2000 Results (As of October 2006) Top 20 SPECint 2000 Top 20 SPECfp 2000 # MHz Processor int peak int base MHz Processor fp peak fp base 1 2933 Core 2 Duo EE 3119 POWER 5+ 3642 3369 2 3000 Xeon 51 xx 3102 Itanium 2 3098 3 2666 Core 2 Duo 2848 51 xx 3056 2811 4 2660 Xeon 30 xx 2835 Duo EE 3050 3048 5 3000 Opteron 2119 30 xx 3044 2763 6 2800 Athlon 64 FX 2061 3017 7 2800 Opteron AM 2 1960 Duo 2850 2847 8 2300 POWER 5+ 1900 2796 2585 9 3733 Pentium 4 E 1872 2497 2260 10 3800 Pentium 4 Xeon 1856 AM 2 2462 2230 Performance relative to a Sun Ultra 5_10 (300 MHz) which is given a score of SPECint 2000 = SPECfp 2000 = 100 11 2260 Pentium M 1839 Source: http: //www. aceshardware. com/SPECmine/top. jsp 4 E 2283 2280 3108 2300 3089 1600 DC 2844 3000 Xeon 2826 2933 Core 2 1942 2660 Xeon 1923 1600 Itanium 2 1749 2667 Core 2 1820 1900 POWER 5 1870 3000 Opteron 1854 2800 Opteron EECC 550 1812 3733 - Shaaban Pentium #25 Lec # 3 Winter 2012 12 -4 -2012

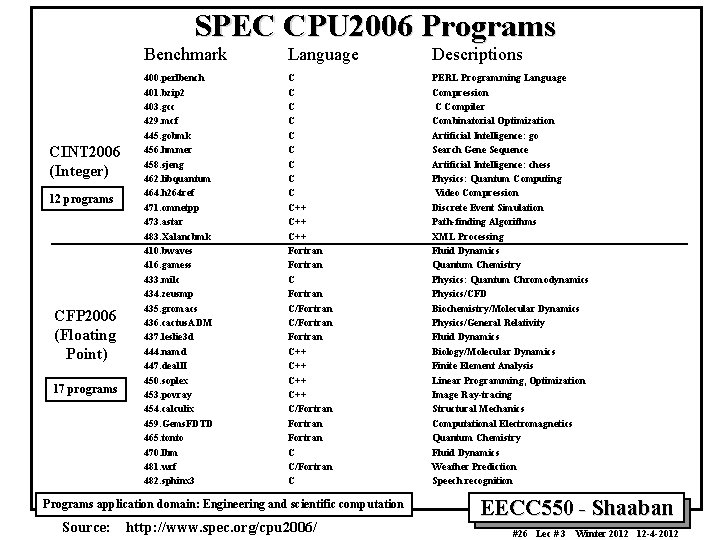
SPEC CPU 2006 Programs CINT 2006 (Integer) 12 programs CFP 2006 (Floating Point) 17 programs Benchmark Language Descriptions 400. perlbench 401. bzip 2 403. gcc 429. mcf 445. gobmk 456. hmmer 458. sjeng 462. libquantum 464. h 264 ref 471. omnetpp 473. astar 483. Xalancbmk 410. bwaves 416. gamess 433. milc 434. zeusmp 435. gromacs 436. cactus. ADM 437. leslie 3 d 444. namd 447. deal. II 450. soplex 453. povray 454. calculix 459. Gems. FDTD 465. tonto 470. lbm 481. wrf 482. sphinx 3 C C C C C++ C++ Fortran C/Fortran C++ C++ C/Fortran C C/Fortran C PERL Programming Language Compression C Compiler Combinatorial Optimization Artificial Intelligence: go Search Gene Sequence Artificial Intelligence: chess Physics: Quantum Computing Video Compression Discrete Event Simulation Path-finding Algorithms XML Processing Fluid Dynamics Quantum Chemistry Physics: Quantum Chromodynamics Physics/CFD Biochemistry/Molecular Dynamics Physics/General Relativity Fluid Dynamics Biology/Molecular Dynamics Finite Element Analysis Linear Programming, Optimization Image Ray-tracing Structural Mechanics Computational Electromagnetics Quantum Chemistry Fluid Dynamics Weather Prediction Speech recognition Programs application domain: Engineering and scientific computation Source: http: //www. spec. org/cpu 2006/ EECC 550 - Shaaban #26 Lec # 3 Winter 2012 12 -4 -2012

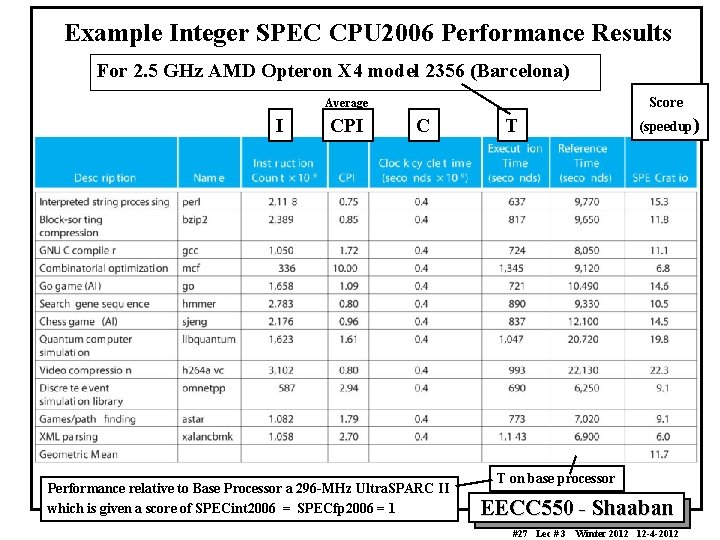
Example Integer SPEC CPU 2006 Performance Results For 2. 5 GHz AMD Opteron X 4 model 2356 (Barcelona) Score Average I CPI C Performance relative to Base Processor a 296 -MHz Ultra. SPARC II which is given a score of SPECint 2006 = SPECfp 2006 = 1 (speedup) T T on base processor EECC 550 - Shaaban #27 Lec # 3 Winter 2012 12 -4 -2012

• Computer Performance Measures : MIPS (Million Instructions Per Second) Rating For a specific program running on a specific CPU the MIPS rating is a measure of how many millions of instructions are executed per second: MIPS Rating = Instruction count / (Execution Time x 106) = Instruction count / (CPU clocks x Cycle time x 106) = (Instruction count x Clock rate) / (Instruction count x CPI x 106) = Clock rate / (CPI x 106) • Major problem with MIPS rating: As shown above the MIPS rating does not account for the count of instructions executed (I). – A higher MIPS rating in many cases may not mean higher performance or better execution time. i. e. due to compiler design variations. • In addition the MIPS rating: – Does not account for the instruction set architecture (ISA) used. • Thus it cannot be used to compare computers/CPUs with different instruction sets. – Easy to abuse: Program used to get the MIPS rating is often omitted. • Often the Peak MIPS rating is provided for a given CPU which is obtained using a program comprised entirely of instructions with the lowest CPI for the given CPU design which does not represent real programs. T = I x CPI x C EECC 550 - Shaaban #28 Lec # 3 Winter 2012 12 -4 -2012

Computer Performance Measures : MIPS (Million Instructions Per Second) Rating • Under what conditions can the MIPS rating be used to compare performance of different CPUs? • The MIPS rating is only valid to compare the performance of different CPUs provided that the following conditions are satisfied: 1 The same program is used (actually this applies to all performance metrics) 2 The same ISA is used 3 The same compiler is used Þ (Thus the resulting programs used to run on the CPUs and obtain the MIPS rating are identical at the machine code (binary) level including the same instruction count) EECC 550 - Shaaban #29 Lec # 3 Winter 2012 12 -4 -2012

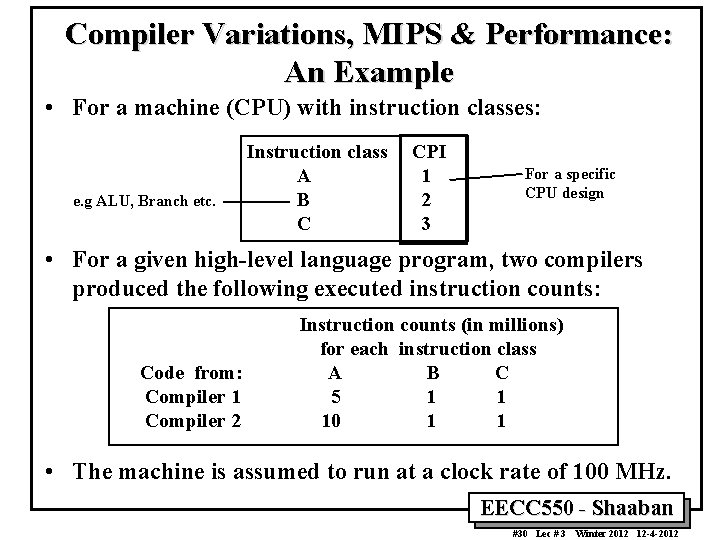
Compiler Variations, MIPS & Performance: An Example • For a machine (CPU) with instruction classes: e. g ALU, Branch etc. Instruction class A B C CPI 1 2 3 For a specific CPU design • For a given high-level language program, two compilers produced the following executed instruction counts: Code from: Compiler 1 Compiler 2 Instruction counts (in millions) for each instruction class A B C 5 1 1 10 1 1 • The machine is assumed to run at a clock rate of 100 MHz. EECC 550 - Shaaban #30 Lec # 3 Winter 2012 12 -4 -2012

Compiler Variations, MIPS & Performance: An Example (Continued) MIPS = Clock rate / (CPI x 106) = 100 MHz / (CPI x 106) CPI = CPU execution cycles / Instructions count CPU time = Instruction count x CPI / Clock rate • For compiler 1: – CPI 1 = (5 x 1 + 1 x 2 + 1 x 3) / (5 + 1) = 10 / 7 = 1. 43 – MIPS Rating 1 = 100 / (1. 428 x 106) = 70. 0 MIPS – CPU time 1 = ((5 + 1) x 106 x 1. 43) / (100 x 106) = 0. 10 seconds • For compiler 2: – CPI 2 = (10 x 1 + 1 x 2 + 1 x 3) / (10 + 1) = 15 / 12 = 1. 25 – MIPS Rating 2 = 100 / (1. 25 x 106) = 80. 0 MIPS – CPU time 2 = ((10 + 1) x 106 x 1. 25) / (100 x 106) = 0. 15 seconds MIPS rating indicates that compiler 2 is better while in reality the code produced by compiler 1 is faster EECC 550 - Shaaban #31 Lec # 3 Winter 2012 12 -4 -2012

MIPS (The ISA not the metric) Loop Performance Example High Memory $6 points here For the loop: X[999] X[998] . . for (i=0; i<1000; i=i+1){ x[i] = x[i] + s; } $2 initially MIPS assembly code is given by: loop: lw addi lw add sw addi bne $3, $6, $4, $5, $2, $6, 0($1) $2, 4000 0($2) $4, $3 0($2) $2, 4 $2, loop Last element to compute points here ; ; ; ; X[0] Low Memory First element to compute load s in $3 $6 = address of last element + 4 load x[i] in $4 $5 has x[i] + s store computed x[i] increment $2 to point to next x[ ] element last loop iteration reached? The MIPS code is executed on a specific CPU that runs at 500 MHz (C = clock cycle = 2 ns = 2 x 10 -9 seconds) with following instruction type CPIs : For this MIPS code running on this CPU find: Instruction type ALU Load Store Branch CPI 4 5 7 3 1 - Fraction of total instructions executed for each instruction type 2 - Total number of CPU cycles 3 - Average CPI 4 - Fraction of total execution time for each instructions type 5 - Execution time 6 - MIPS rating , peak MIPS rating for this CPU X[ ] array of words in memory, base address in $2 , s a constant word value in memory, address in $1 EECC 550 - Shaaban #32 Lec # 3 Winter 2012 12 -4 -2012

MIPS (The ISA) Loop Performance Example (continued) • • The code has 2 instructions before the loop and 5 instructions in the body of the loop which iterates 1000 times, Thus: Total instructions executed, I = 5 x 1000 + 2 = 5002 instructions 1 Number of instructions executed/fraction Fi for each instruction type: – – ALU instructions = 1 + 2 x 1000 = 2001 Load instructions = 1 + 1 x 1000 = 1001 Store instructions = 1000 Branch instructions = 1000 CPIALU = 4 Fraction. ALU = FALU = 2001/5002 = 0. 4 = 40% CPILoad = 5 Fraction. Load = FLoad = 1001/5002= 0. 2 = 20% CPIStore = 7 Fraction. Store = FStore = 1000/5002 = 0. 2 = 20% CPIBranch = 3 Fraction. Branch= FBranch = 1000/5002= 0. 2 = 20% 2 3 4 = 2001 x 4 + 1001 x 5 + 1000 x 7 + 1000 x 3 = 23009 cycles Average CPI = CPU clock cycles / I = 23009/5002 = 4. 6 Instruction type Fraction of execution time for each instruction type: – – CPI ALU Load Store Branch Fraction of time for ALU instructions = CPIALU x FALU / CPI= 4 x 0. 4/4. 6 = 0. 348 = 34. 8% Fraction of time for load instructions = CPIload x Fload / CPI= 5 x 0. 2/4. 6 = 0. 217 = 21. 7% Fraction of time for store instructions = CPIstore x Fstore / CPI= 7 x 0. 2/4. 6 = 0. 304 = 30. 4% Fraction of time for branch instructions = CPIbranch x Fbranch / CPI= 3 x 0. 2/4. 6 = 0. 13 = 13% 4 5 7 3 5 Execution time = I x CPI x C = CPU cycles x C = 23009 x 2 x 10 -9 = = 4. 6 x 10 -5 seconds = 0. 046 msec = 46 usec 6 MIPS rating = Clock rate / (CPI x 106) = 500 / 4. 6 = 108. 7 MIPS – The CPU achieves its peak MIPS rating when executing a program that only has instructions of the type with the lowest CPI. In this case branches with CPIBranch = 3 – Peak MIPS rating = Clock rate / (CPIBranch x 106) = 500/3 = 166. 67 MIPS EECC 550 - Shaaban #33 Lec # 3 Winter 2012 12 -4 -2012

Computer Performance Measures : MFLOPS (Million FLOating-Point Operations Per Second) • • A floating-point operation is an addition, subtraction, multiplication, or division operation applied to numbers represented by a single or a double precision floating-point representation. MFLOPS, for a specific program running on a specific computer, is a measure of millions of floating point-operation (megaflops) per second: MFLOPS = Number of floating-point operations / (Execution time x 106 ) • • • MFLOPS rating is a better comparison measure between different machines (applies even if ISAs are different) than the MIPS rating. – Applicable even if ISAs are different Program-dependent: Different programs have different percentages of floating -point operations present. i. e compilers have no floating- point operations and yield a MFLOPS rating of zero. Dependent on the type of floating-point operations present in the program. – Peak MFLOPS rating for a CPU: Obtained using a program comprised entirely of the simplest floating point instructions (with the lowest CPI) for the given CPU design which does not represent real floating point programs. Current peak MFLOPS rating: 8, 000 -20, 000 MFLOPS (8 -20 GFLOPS) per processor core EECC 550 - Shaaban #34 Lec # 3 Winter 2012 12 -4 -2012

Quantitative Principles of Computer Design • Amdahl’s Law: The performance gain from improving some portion of a computer is calculated by: i. e using some enhancement Speedup = Performance for entire task using the enhancement Performance for the entire task without using the enhancement Before Enhancement or Speedup = Execution time without the enhancement Execution time for entire task using the enhancement After Enhancement Here: Task = Program 4 th Edition: Chapter 1. 8 Recall: Performance = 1 /Execution Time 3 rd Edition: Chapter 4. 5 EECC 550 - Shaaban #35 Lec # 3 Winter 2012 12 -4 -2012

Performance Enhancement Calculations: Amdahl's Law • The performance enhancement possible due to a given design improvement is limited by the amount that the improved feature is used • Amdahl’s Law: Performance improvement or speedup due to enhancement E: Execution Time without E Speedup(E) = -------------------Execution Time with E original Performance with E = ----------------Performance without E – Suppose that enhancement E accelerates a fraction F of the execution time by a factor S and the remainder of the time is unaffected then: Execution Time with E = ((1 -F) + F/S) X Execution Time without E Hence speedup is given by: Execution Time without E 1 Speedup(E) = ----------------------------- = ----------((1 - F) + F/S) X Execution Time without E (1 - F) + F/S F (Fraction of execution time enhanced) refers to original execution time before the enhancement is applied EECC 550 - Shaaban #36 Lec # 3 Winter 2012 12 -4 -2012

Pictorial Depiction of Amdahl’s Law Enhancement E accelerates fraction F of original execution time by a factor of S Before: Execution Time without enhancement E: (Before enhancement is applied) • shown normalized to 1 = (1 -F) + F =1 Unaffected fraction: (1 - F) Affected fraction: F Unchanged Unaffected fraction: (1 - F) After: Execution Time with enhancement E: F/S What if the fraction given is after the enhancement has been applied? How would you solve the problem? (i. e find expression for speedup) Execution Time without enhancement E 1 Speedup(E) = --------------------------- = ---------Execution Time with enhancement E (1 - F) + F/S EECC 550 - Shaaban #37 Lec # 3 Winter 2012 12 -4 -2012

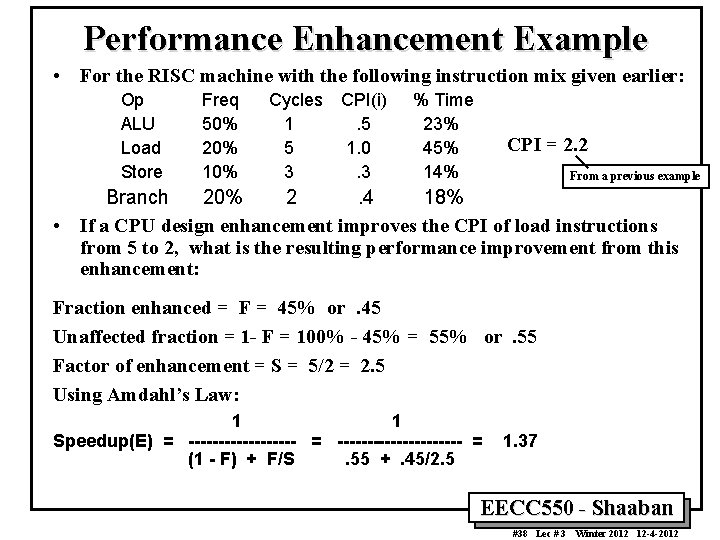
Performance Enhancement Example • For the RISC machine with the following instruction mix given earlier: Op ALU Load Store Freq 50% 20% 10% Cycles 1 5 3 CPI(i). 5 1. 0. 3 % Time 23% 45% 14% CPI = 2. 2 From a previous example Branch 20% 2. 4 18% • If a CPU design enhancement improves the CPI of load instructions from 5 to 2, what is the resulting performance improvement from this enhancement: Fraction enhanced = F = 45% or. 45 Unaffected fraction = 1 - F = 100% - 45% = 55% or. 55 Factor of enhancement = S = 5/2 = 2. 5 Using Amdahl’s Law: 1 1 Speedup(E) = --------------------- = (1 - F) + F/S. 55 +. 45/2. 5 1. 37 EECC 550 - Shaaban #38 Lec # 3 Winter 2012 12 -4 -2012

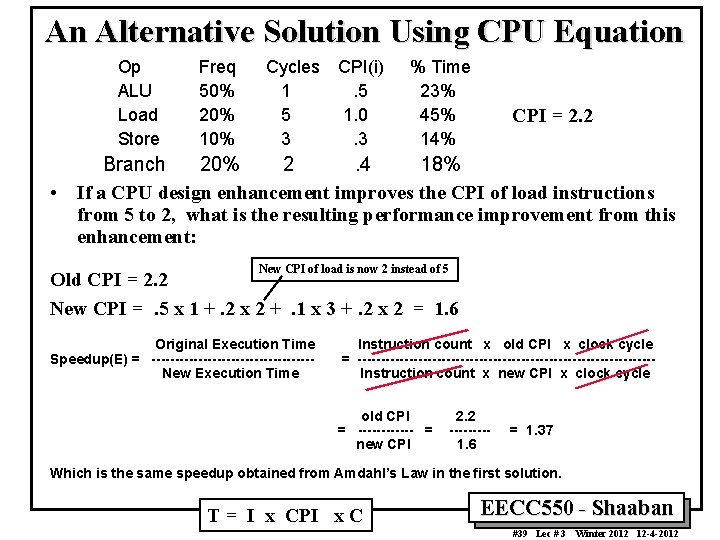
An Alternative Solution Using CPU Equation Op ALU Load Store Freq 50% 20% 10% Cycles 1 5 3 CPI(i). 5 1. 0. 3 % Time 23% 45% 14% CPI = 2. 2 Branch 20% 2. 4 18% • If a CPU design enhancement improves the CPI of load instructions from 5 to 2, what is the resulting performance improvement from this enhancement: New CPI of load is now 2 instead of 5 Old CPI = 2. 2 New CPI =. 5 x 1 +. 2 x 2 +. 1 x 3 +. 2 x 2 = 1. 6 Original Execution Time Speedup(E) = -----------------New Execution Time Instruction count x old CPI x clock cycle = --------------------------------Instruction count x new CPI x clock cycle old CPI = ------ = new CPI 2. 2 ----1. 6 = 1. 37 Which is the same speedup obtained from Amdahl’s Law in the first solution. T = I x CPI x C EECC 550 - Shaaban #39 Lec # 3 Winter 2012 12 -4 -2012

Performance Enhancement Example • A program runs in 100 seconds on a machine with multiply operations responsible for 80 seconds of this time. By how much must the speed of multiplication be improved to make the program four times faster? Desired speedup = 4 = ® ® ® 100 --------------------------Execution Time with enhancement Execution time with enhancement = 100/4 = 25 seconds = (100 - 80 seconds) + 80 seconds / S 25 seconds = 20 seconds + 80 seconds / S 5 = 80 seconds / S S = 80/5 = 16 Alternatively, it can also be solved by finding enhanced fraction of execution time: F = 80/100 =. 8 and then solving Amdahl’s speedup equation for desired enhancement factor S 1 Speedup(E) = --------- = 4 = (1 - F) + F/S 1 1 --------- = -------(1 -. 8) +. 8/S. 2 +. 8/s Hence multiplication should be 16 times faster to get an overall speedup of 4. Machine = CPU Solving for S gives S= 16 EECC 550 - Shaaban #40 Lec # 3 Winter 2012 12 -4 -2012

Performance Enhancement Example • For the previous example with a program running in 100 seconds on a machine with multiply operations responsible for 80 seconds of this time. By how much must the speed of multiplication be improved to make the program five times faster? Desired speedup = 5 = ® 100 --------------------------Execution Time with enhancement Execution time with enhancement = 100/5 = 20 seconds = (100 - 80 seconds) + 80 seconds / s 20 seconds = 20 seconds + 80 seconds / s ® 0 = 80 seconds / s No amount of multiplication speed improvement can achieve this. EECC 550 - Shaaban #41 Lec # 3 Winter 2012 12 -4 -2012

Extending Amdahl's Law To Multiple Enhancements n enhancements each affecting a different portion of execution time • Suppose that enhancement Ei accelerates a fraction Fi of the original execution time by a factor Si and the remainder of the time is unaffected then: i = 1, 2, …. n Unaffected fraction What if the fractions given are after the enhancements were applied? How would you solve the problem? (i. e find expression for speedup) Note: All fractions Fi refer to original execution time before the enhancements are applied. EECC 550 - Shaaban #42 Lec # 3 Winter 2012 12 -4 -2012

Amdahl's Law With Multiple Enhancements: Example • Three CPU performance enhancements are proposed with the following speedups and percentage of the code original execution time affected: Speedup 1 = S 1 = 10 Speedup 2 = S 2 = 15 Speedup 3 = S 3 = 30 • • • Percentage 1 = F 1 = 20% Percentage 1 = F 2 = 15% Percentage 1 = F 3 = 10% While all three enhancements are in place in the new design, each enhancement affects a different portion of the code and only one enhancement can be used at a time. What is the resulting overall speedup? Speedup = 1 / [(1 -. 2 -. 15 -. 1) +. 2/10 +. 15/15 +. 1/30)] = 1/ [. 55 +. 0333 ] = 1 /. 5833 = 1. 71 EECC 550 - Shaaban #43 Lec # 3 Winter 2012 12 -4 -2012

Pictorial Depiction of Example Before: Execution Time with no enhancements: 1 Unaffected, fraction: . 55 i. e normalized to 1 S 1 = 10 F 1 =. 2 S 2 = 15 S 3 = 30 F 2 =. 15 F 3 =. 1 / 15 / 10 / 30 Unchanged Unaffected, fraction: . 55 After: Execution Time with enhancements: . 55 +. 02 +. 01 +. 00333 =. 5833 What if the fractions given are after the enhancements were applied? How would you solve the problem? Speedup = 1 /. 5833 = 1. 71 Note: All fractions Fi refer to original execution time. EECC 550 - Shaaban #44 Lec # 3 Winter 2012 12 -4 -2012

“Reverse” Multiple Enhancements Amdahl's Law • • Multiple Enhancements Amdahl's Law assumes that the fractions given refer to original execution time. If for each enhancement Si the fraction Fi it affects is given as a fraction of the resulting execution time after the enhancements were applied then: Unaffected fraction i. e as if resulting execution time is normalized to 1 • For the previous example assuming fractions given refer to resulting execution time after the enhancements were applied (not the original execution time), then: Speedup = (1 -. 2 -. 15 -. 1) +. 2 x 10 +. 15 x 15 +. 1 x 30 =. 55 + 2. 25 + 3 = 7. 8 Find original fractions? EECC 550 - Shaaban #45 Lec # 3 Winter 2012 12 -4 -2012