Conservation Theorems Sect 2 5 Discussion of conservation

Conservation Theorems: Sect. 2. 5 • Discussion of conservation of Single Particle Only! – Linear Momentum – Angular Momentum – Total (Mechanical) Energy • Not new Laws! Direct consequences of Newton’s Laws! “Conserved” “A constant”

Linear Momentum • The total linear momentum p = mv of a particle is conserved when the total force acting on it is zero. • Proof: Start with Newton’s 2 nd Law: F = (dp/dt) (1) If F = 0 (1) (dp/dt) = 0 p = constant (2) (time independent) • (2) is a vector relation. It applies component by component.

• An alternative formulation: Let s a constant vector such that the component of the total force F along the s direction vanishes. F s = 0 Newton’s 2 nd Law (dp/dt) s = 0 p s = constant The component of linear momentum in a direction in which the force vanishes is a constant in time.

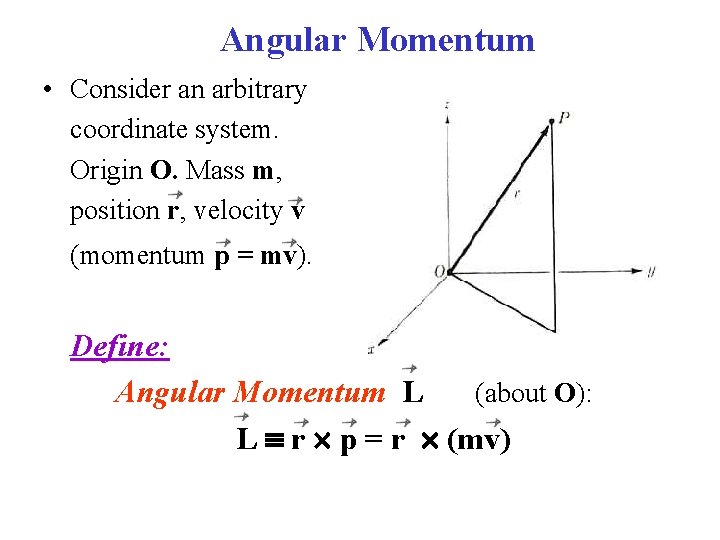
Angular Momentum • Consider an arbitrary coordinate system. Origin O. Mass m, position r, velocity v (momentum p = mv). Define: Angular Momentum L (about O): L r p = r (mv)

• Consider an arbitrary coordinate system. Origin O. Mass m, position r, velocity v (momentum p = mv). Define: Torque (moment of force) N (about O): N r F = r (dp/dt) = r [d(mv)/dt] Newton’s 2 nd Law!

• So: L = r p, N = r F • From Newton’s 2 nd Law: N = r (dp/dt) = r m(dv/dt) • Consider the time derivative of L: (d. L/dt) = d(r p)/dt = (dr/dt) p + r (dp/dt) = v mv + r (dp/dt) = 0 + N or: (d. L/dt) = N This is Newton’s 2 nd Law - Rotational motion version!

N = d. L/dt • If no torques act on the particle, N=0 L = constant d. L/dt = 0 (time independent) • The total angular momentum L = r mv of a particle is conserved when the total torque acting on it is zero. • Reminder: Choice of origin is arbitrary! A careful choice can save effort in solving a problem!

Work & Energy • Definition: A particle is acted on by a total force F. The Work done on the particle in moving it from (arbitrary) position 1 to (arbitrary) position 2 in space is defined as line integral (limits from 1 to 2): W 12 ∫ F dr • By Newton’s 2 nd Law (using chain rule of differentiation): F dr = (dp/dt) (dr/dt) dt = m(dv/dt) v dt = (½)m [d(v v)/dt] dt = (½)m (dv 2/dt) dt = [d{(½)mv 2}/dt] dt = d[(½)mv 2] W 12 = ∫[d{(½)mv 2}/dt] dt = ∫d{(½)mv 2}

Kinetic Energy W 12 = ∫d{(½)mv 2} = (½)m(v 2)2 – (½) m(v 1)2 • Defining the Kinetic Energy of the particle: T (½)mv 2 , This becomes: W 12 = T 2 -T 1 = T The work done by the total force on a particle is equal to the change in the particle’s kinetic energy. The Work-Energy Theorem.

• Look at the work integral: W 12 = ∫F dr • Often, the work done by F in going from 1 to 2 is independent of the path taken from 1 to 2: • In such cases, F is said to be a If F is conservative, W 12 is the same for paths a, b, c, & all others! Conservative Force. • For conservative forces, one can define a Potential Energy U.

Potential Energy • For conservative forces, (& only for conservative forces!) we define a Potential Energy function U(r). By definition: W 12 ∫F dr U 1 - U 2 - U • The Potential Energy of a particle = its capacity to do work (conservative forces only!). The work done in moving the particle from 1 to 2 = - change in potential energy.

• For conservative forces ∫F dr = U 1 - U 2 - U (1) • Math: This can be satisfied if & only if the force has the form: F - U (2) – (1) & (2) will hold if U = U(r, t) only (& not for U = U(r, v, t)) – Note: potential energy is defined only to within an additive constant because force = derivative of potential energy! Absolute potential energy has no meaning! – Similarly, because the velocity of a particle changes from one inertial frame to another, absolute kinetic energy has no meaning!

Mechanical Energy Conservation • • • In general: W 12 = ∫F dr KE Definition: T (½)mv 2 Work-Energy Theorem: W 12 = T 2 -T 1 = T Conservative Forces F: W 12= U 1 - U 2 = - U Combining gives: T = - U or T 2 -T 1 = U 1 - U 2 or T + U = 0 or T 1 + U 1 = T 2 + U 2 For conservative forces, the sum of the kinetic and potential energies of a particle is a constant. T + U = constant Conservation of kinetic plus potential energy.

• Define: Total (Mechanical) Energy of a particle (in the presence of conservative forces): E T+U • We just showed that (for conservative forces) the total mechanical energy is conserved (const. , time independent). • Can show this another way. Consider the total time derivative: (d. E/dt) = (d. T/dt) + (d. U/dt) • From previous results: d. T = d[(½)mv 2] = F dr (d. T/dt) = F (dr/dt) = F r = F v • Also (assuming U = U(r, t) & using chain rule) (d. U/dt) = ∑i (∂U/∂xi)(dxi/dt) + (∂U/∂t)

• Rewriting (using the definition of ): (d. U/dt) = U v + (∂U/∂t) • So: (d. E/dt) = (d. T/dt) + (d. U/dt) or (d. E/dt) = F v + U v + (∂U/∂t) • But, F = - U The first 2 terms cancel & we have: (d. E/dt) = (∂U/∂t) If U is not an explicit function of time, (∂U/∂t) = 0 = (d. E/dt) E = T + U = constant

SUMMARY The total mechanical energy E of a particle in a conservative force field is a constant in time. • Note: We have not proven conservation laws! We have derived them using Newton’s Laws under certain conditions. They aren’t new Laws, but just Newton’s Laws in a different language.

Conservation Laws • Brief Philosophical Discussion (p. 81): Conservation “postulates” rather than “Laws”? Physicists now insist that any physical theory satisfy conservation laws in order for it to be valid. • For example, introduce different kinds of energy into a theory to ensure that conservation of energy holds. (e. g. , Energy in EM field). • Consistent with experimental facts!

Conservation Laws & Symmetry Principles (not in text!) In all of physics (not just mechanics) it can be shown: – Each Conservation Law implies an underlying symmetry of the system. – Conversely, each system symmetry implies a Conservation Law: Can show: Translational Symmetry Linear Momentum Conservation Rotational Symmetry Angular Momentum Conservation Time Reversal Symmetry Energy Conservation Inversion Symmetry Parity Conservation (Parity is a concept in QM!)