Circuiti in corrente alternata Carica e scarica di







- Slides: 15

Circuiti in corrente alternata Carica e scarica di condensatori e di induttanze Circuiti oscillanti Equazioni di Maxwell

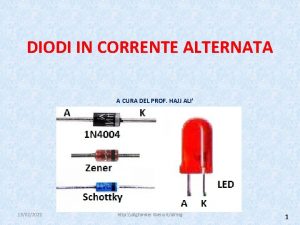
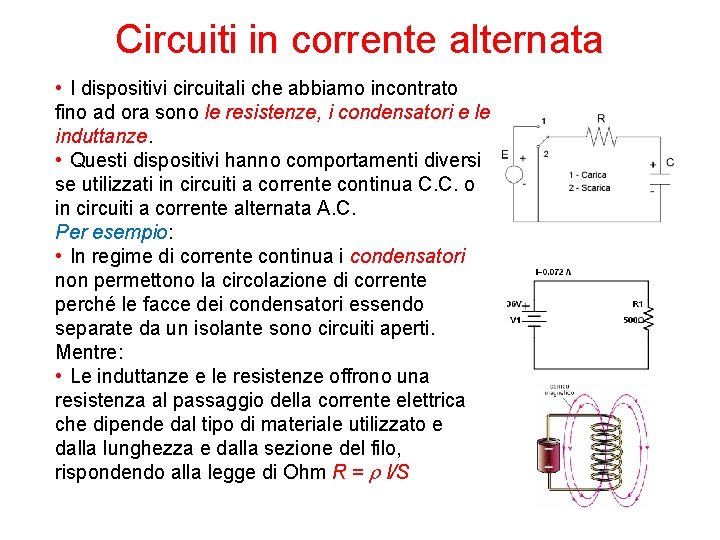
Circuiti in corrente alternata • I dispositivi circuitali che abbiamo incontrato fino ad ora sono le resistenze, i condensatori e le induttanze. • Questi dispositivi hanno comportamenti diversi se utilizzati in circuiti a corrente continua C. C. o in circuiti a corrente alternata A. C. Per esempio: • In regime di corrente continua i condensatori non permettono la circolazione di corrente perché le facce dei condensatori essendo separate da un isolante sono circuiti aperti. Mentre: • Le induttanze e le resistenze offrono una resistenza al passaggio della corrente elettrica che dipende dal tipo di materiale utilizzato e dalla lunghezza e dalla sezione del filo, rispondendo alla legge di Ohm R = r l/S

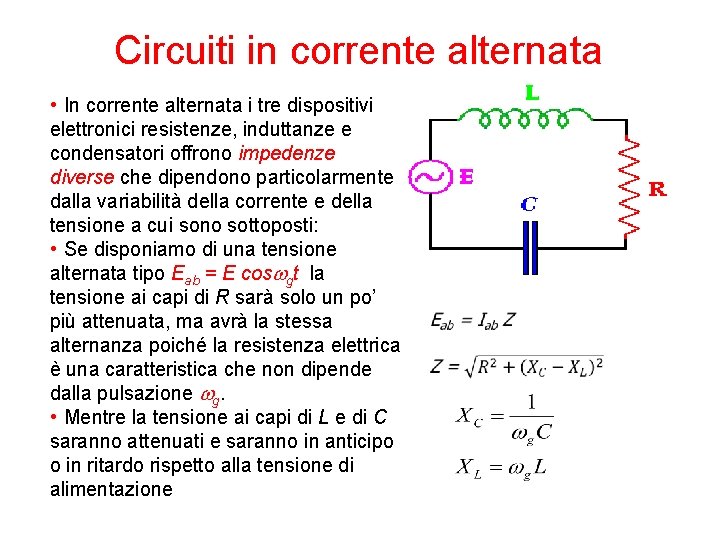
Circuiti in corrente alternata • In corrente alternata i tre dispositivi elettronici resistenze, induttanze e condensatori offrono impedenze diverse che dipendono particolarmente dalla variabilità della corrente e della tensione a cui sono sottoposti: • Se disponiamo di una tensione alternata tipo Eab = E coswgt la tensione ai capi di R sarà solo un po’ più attenuata, ma avrà la stessa alternanza poiché la resistenza elettrica è una caratteristica che non dipende dalla pulsazione wg. • Mentre la tensione ai capi di L e di C saranno attenuati e saranno in anticipo o in ritardo rispetto alla tensione di alimentazione

Carica di un condesatore • Con l’interruttore S in a il condensatore C si carica fino al valore della f. e. m. E e la carica accumulata ai suoi capi è q = EC. • Come variano, nel tempo, la corrente i, la carica q e la tensione Vc ai capi di C ? • Per la legge delle maglie E - i. R – q/C = 0 q = C E [1 – e -t/(RC)] (fase di carica) • La corrente di carica è dq/dt = E/R [e - t/(RC)] • Da q = CV si può ricavare VC = E [1 – e -t/(RC)] • Il prodotto RC ha le dimensioni di un tempo, ed è chiamata costante di tempo t, ed è il tempo necessario a caricare il condensatore fino al 63%

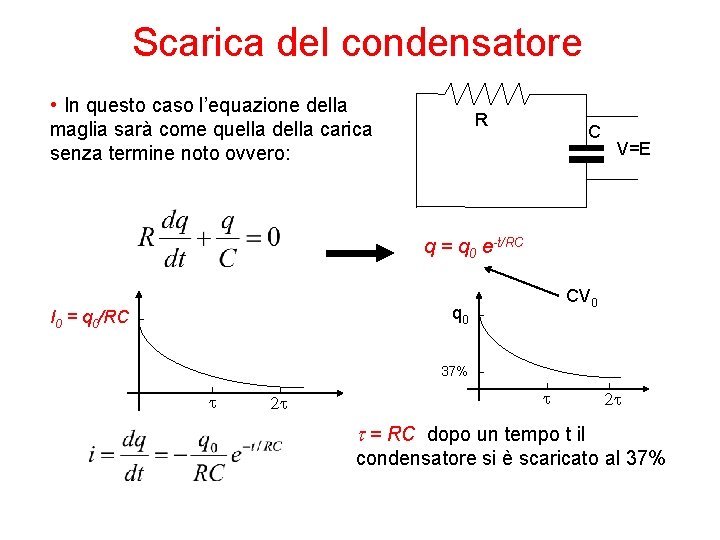
Scarica del condensatore • In questo caso l’equazione della maglia sarà come quella della carica senza termine noto ovvero: R C V=E q = q 0 e-t/RC CV 0 q 0 I 0 = q 0/RC 37% t 2 t t = RC dopo un tempo t il condensatore si è scaricato al 37%

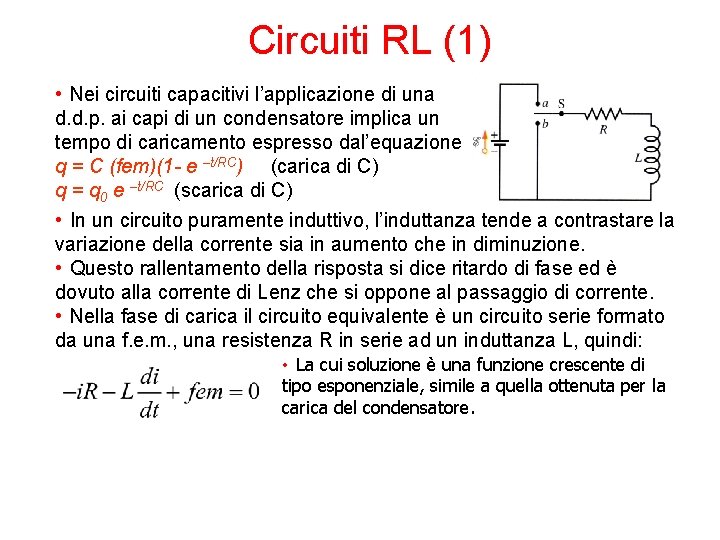
Circuiti RL (1) • Nei circuiti capacitivi l’applicazione di una d. d. p. ai capi di un condensatore implica un tempo di caricamento espresso dal’equazione q = C (fem)(1 - e –t/RC) (carica di C) q = q 0 e –t/RC (scarica di C) • In un circuito puramente induttivo, l’induttanza tende a contrastare la variazione della corrente sia in aumento che in diminuzione. • Questo rallentamento della risposta si dice ritardo di fase ed è dovuto alla corrente di Lenz che si oppone al passaggio di corrente. • Nella fase di carica il circuito equivalente è un circuito serie formato da una f. e. m. , una resistenza R in serie ad un induttanza L, quindi: • La cui soluzione è una funzione crescente di tipo esponenziale, simile a quella ottenuta per la carica del condensatore.

Circuiti RL (2) • La soluzione dell’equazione del circuito induttivo ha un andamento esponenziale analogo a quello del circuito capacitivo. • La differenza è che nei circuiti induttivi cresce il potenziale V mentre nei circuiti capacitivi cresce la carica q. • La scarica dell’induttanza ha un andamento esponenziale decrescente e si realizza inserendo il dispositivo in serie ad una resistenza. carica di L scarica di L

Energia di un condensatore • Per caricare un condensatore serve energia. • Tale energia serve per vincere la forza repulsiva generata dalle cariche precedentemente immagazzinate nel condensatore. • Se q’ è la i-esima carica accumulata dal condensatore il suo potenziale sarà V’ = q’/C. • L’incremento di una successiva quantità di carica dq’ richiederà un lavoro d. L = V’dq’ ovvero d. L = (1/C)q’dq’ • Pertanto il Lavoro w necessario a caricare un condensatore è • Questo è il modulo dell’energia elettrica che viene immagazzinata nel condensatore U = ½ CV 2 + -

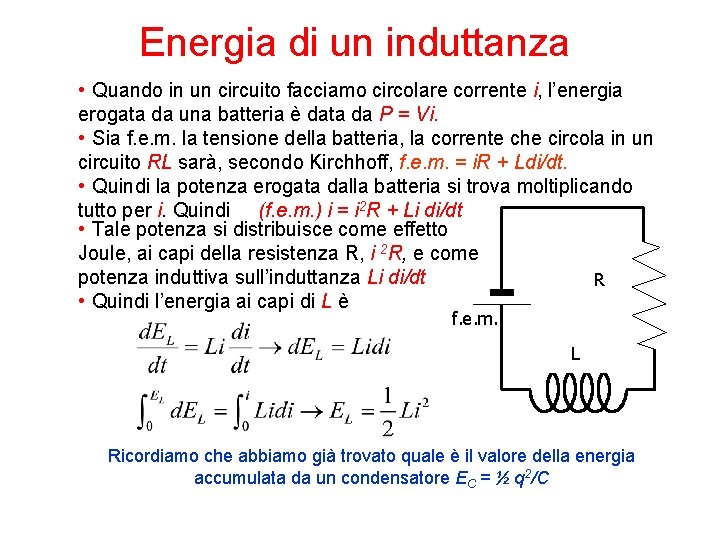
Energia di un induttanza • Quando in un circuito facciamo circolare corrente i, l’energia erogata da una batteria è data da P = Vi. • Sia f. e. m. la tensione della batteria, la corrente che circola in un circuito RL sarà, secondo Kirchhoff, f. e. m. = i. R + Ldi/dt. • Quindi la potenza erogata dalla batteria si trova moltiplicando tutto per i. Quindi (f. e. m. ) i = i 2 R + Li di/dt • Tale potenza si distribuisce come effetto Joule, ai capi della resistenza R, i 2 R, e come potenza induttiva sull’induttanza Li di/dt R • Quindi l’energia ai capi di L è f. e. m. L Ricordiamo che abbiamo già trovato quale è il valore della energia accumulata da un condensatore EC = ½ q 2/C

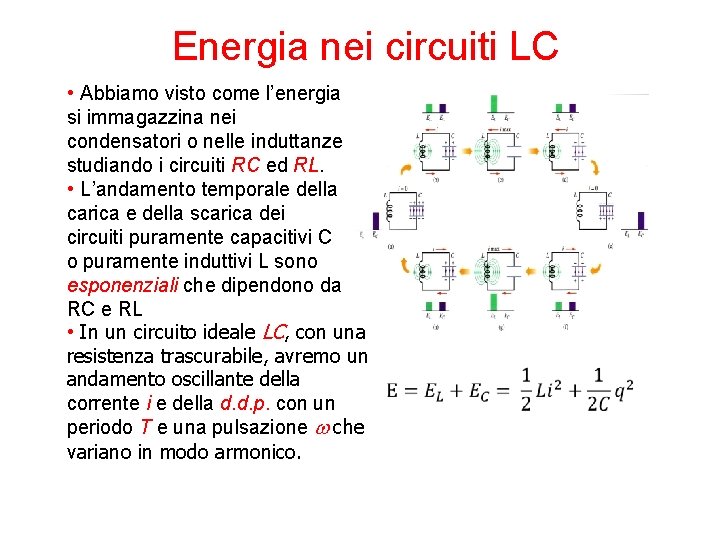
Energia nei circuiti LC • Abbiamo visto come l’energia si immagazzina nei condensatori o nelle induttanze studiando i circuiti RC ed RL. • L’andamento temporale della carica e della scarica dei circuiti puramente capacitivi C o puramente induttivi L sono esponenziali che dipendono da RC e RL • In un circuito ideale LC, con una resistenza trascurabile, avremo un andamento oscillante della corrente i e della d. d. p. con un periodo T e una pulsazione w che variano in modo armonico.

Oscillazioni LC • Una massa collegata ad una molla ha un moto oscillatorio come la corrente in un circuito LC. E = Kb + Um = ½ mv 2 + ½ kx 2 E = EL + EC = ½ Li 2 + ½ Q 2/C • La derivata prima della carica nel tempo ci fornisce la corrente dq/dt = - I sin(wt+f) dove I = w. Q ovvero l’ampiezza massima della corrente • Mentre la pulsazione w si ricava dalla derivata seconda di q d 2 q/dt 2 = - w 2 Qcos(wt+f) che sostituita nella formula inquadrata ci da -Lw 2 Qcos(wt+f)+1/C Qcos(wt+f) = 0 Lw 2 = 1/C w 2 = 1/LC • In conclusione: disponendo di un circuito induttivo-capacitivo con un condensatore precaricato oscillerà con frequenza w data da w = 1/√LC

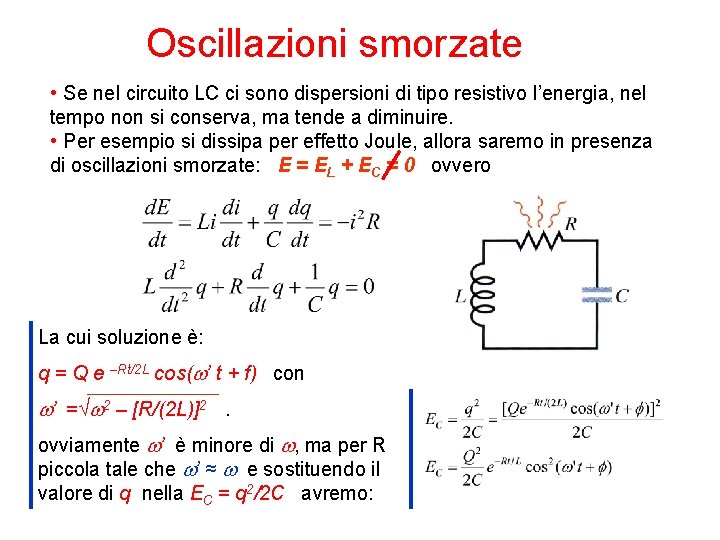
Oscillazioni smorzate • Se nel circuito LC ci sono dispersioni di tipo resistivo l’energia, nel tempo non si conserva, ma tende a diminuire. • Per esempio si dissipa per effetto Joule, allora saremo in presenza di oscillazioni smorzate: E = EL + EC = 0 ovvero La cui soluzione è: q = Q e –Rt/2 L cos(w’ t + f) con w’ =√w 2 – [R/(2 L)]2. ovviamente w’ è minore di w, ma per R piccola tale che w’ ≈ w e sostituendo il valore di q nella EC = q 2/2 C avremo:

Oscillazioni forzate • Un circuito RLC è un circuito in cui è possibile avere oscillazioni periodiche della carica, della tensione o della corrente. La frequenza o meglio la pulsazione angolare è data da w = 1/√LC e questa è la pulsazione propria del circuito. • Esiste però anche la possibilità di imporre una frequenza esterna al circuito, in questo caso ciascun elemento del circuito seguirà la pulsazione esterna e risponderà come i singoli componenti del circuito. • La tensione e la corrente ai capi della resistenza saranno in fase e valgono v. R = VR sin wgt i. R = (VR /R) sin wgt • Ai capi del dispositivo capacitivo v. C = IC XC e i. C = IC sin (wgt –f) con XC = 1/wg. C • Ai capi dell’induttanza v. L = L di. L/dt e i. L = IL sin (wgt –f) XL = wg. L • La combinazione delle risposte dei tre dispositivi è • I = (f. e. m. ) / √(R 2 + (wg. L -1/wg. C)2

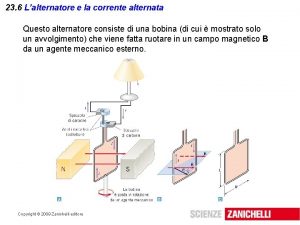
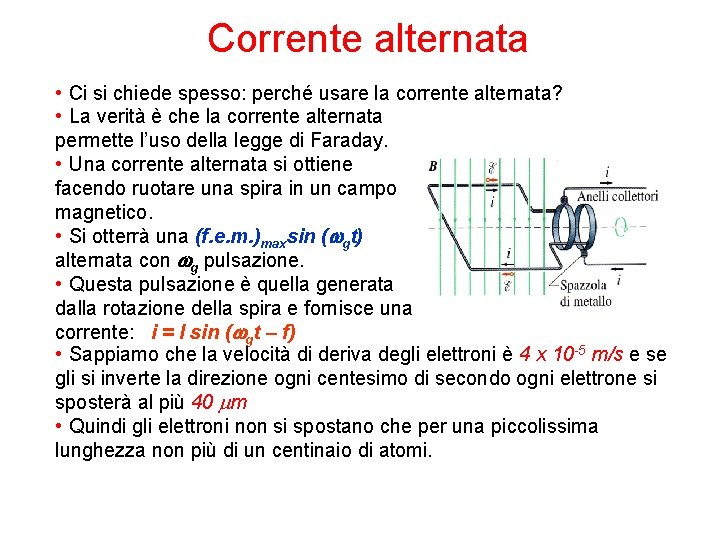
Corrente alternata • Ci si chiede spesso: perché usare la corrente alternata? • La verità è che la corrente alternata permette l’uso della legge di Faraday. • Una corrente alternata si ottiene facendo ruotare una spira in un campo magnetico. • Si otterrà una (f. e. m. )maxsin (wgt) alternata con wg pulsazione. • Questa pulsazione è quella generata dalla rotazione della spira e fornisce una corrente: i = I sin (wgt – f) • Sappiamo che la velocità di deriva degli elettroni è 4 x 10 -5 m/s e se gli si inverte la direzione ogni centesimo di secondo ogni elettrone si sposterà al più 40 mm • Quindi gli elettroni non si spostano che per una piccolissima lunghezza non più di un centinaio di atomi.

Equazioni di Maxwell Teorema di Gauss per l’elettricità Teorema di Gauss per il magnetismo Legge dell’induzione di Faraday Teorema di Ampere generalizzato Dopo un po’ di manipolazioni algebriche omettiamo perché non previsti negli obiettivi di questo corso ricaviamo l’andamento ondulatorio dei campi elettrici e dei capi magnetici
 Modello dei circuiti della gestione
Modello dei circuiti della gestione Simulatore spice
Simulatore spice Circuiti integrati logici
Circuiti integrati logici Circuiti combinatori
Circuiti combinatori Circuiti di comando
Circuiti di comando Circuiti logici sommatori
Circuiti logici sommatori Circuiti penitenziari
Circuiti penitenziari Circuiti fronto sottocorticali
Circuiti fronto sottocorticali Sistema sequenziale esempio
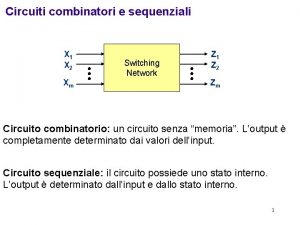
Sistema sequenziale esempio Circuiti combinatori e sequenziali
Circuiti combinatori e sequenziali Classificazione istituti penitenziari
Classificazione istituti penitenziari Strofe e versi
Strofe e versi Segregazione alternata e adiacente
Segregazione alternata e adiacente Esempi di poesie
Esempi di poesie Segregazione alternata
Segregazione alternata Fixed film reactor
Fixed film reactor