Cinemtica y dinmica del movimiento armnico simple m

Cinemática y dinámica del movimiento armónico simple (m. a. s. ) Rafael López-Gay I. E. S. Nicolás Salmerón 1

Un objeto describe un m. a. s. cuando la ecuación de la posición en función del tiempo es: xt=A·cosωt n n n El coseno toma valores entre +1 (cos 0, cos 2π, cos 4π…) y -1 (cosπ, cos 3π, cos 5π…). Por tanto, la posición en un m. a. s. cambiará entre +A y –A. El coseno vuelve a tomar el mismo valor cuando el “ángulo” aumenta en 2π, 4π, 6π… El tiempo mínimo (T) para que la posición en un m. a. s. vuelva a ser la misma debe cumplir: ωT=2π. Es decir: T=2π/ω En un m. a. s. : n n A se llama amplitud (se mide en m en el S. I. ) e indica el valor máximo de x ω se llama frecuencia angular (en rad/s) T=2π/ω se llama periodo (en s) e indica el tiempo empleado en cada vibración f=1/T se llama frecuencia (en s-1 o hertzios) e indica el número de vibraciones cada segundo 2

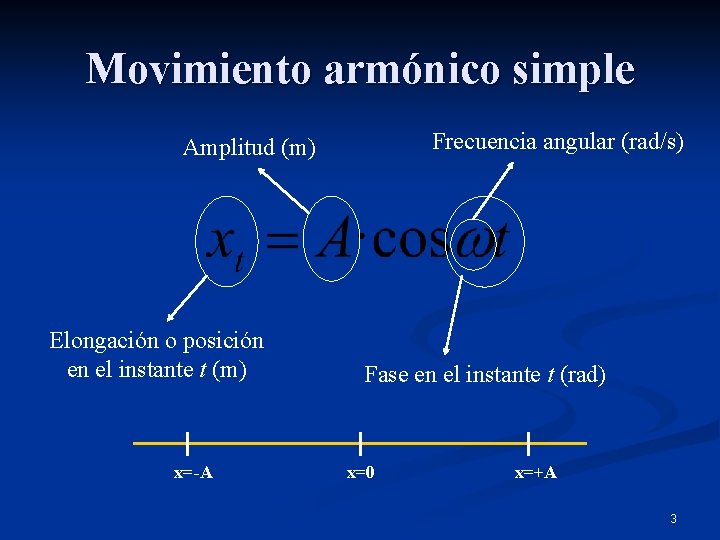
Movimiento armónico simple Frecuencia angular (rad/s) Amplitud (m) Elongación o posición en el instante t (m) x=-A Fase en el instante t (rad) x=0 x=+A 3

Cinemática del m. a. s. n n xt=A·cosωt La posición inicial es A, la posición máxima ±A Derivando: vt=-A·ω·senωt La rapidez inicial es 0, la rapidez máxima ±A·ω Derivando: at=-A·ω2·cosωt La aceleración inicial es –A·ω2, la aceleración máxima ±A·ω2 Como puede apreciarse: a=-ω2·x x=-A v=0 a=+ω2·A x=0 v=±ω·A a=0 x=+A v=0 a=-ω2·A 4

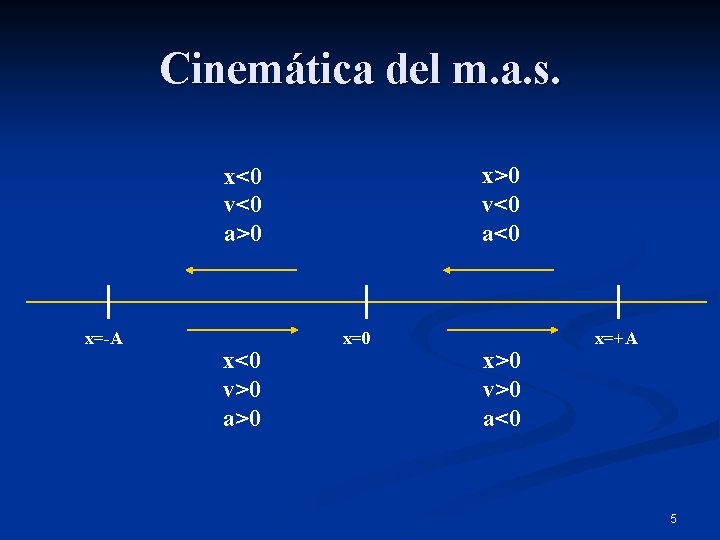
Cinemática del m. a. s. x>0 v<0 a<0 x<0 v<0 a>0 x=-A x<0 v>0 a>0 x=0 x>0 v>0 a<0 x=+A 5

Dinámica del m. a. s. n Un objeto de masa m que describe un m. a. s. está sometido a la acción de una fuerza resultante en la dirección del eje X : Fres=m·a n En función del tiempo: Fres=-m·A·ω2·cosωt n En función de la posición: Fres=-m·ω2·x Es decir, la fuerza resultante en un m. a. s es de tipo elástico: Fres=-k··x (k=m·ω2) n El valor mínimo de la fuerza resultante es cero y el valor máximo ±m·A·ω2 6

Cuando un objeto de masa m se encuentra sometido a la acción de una fuerza elástica: F=-k·x (por ejemplo, si está sujeto al extremo de un muelle), describirá un m. a. s: xt=A·cosωt, de amplitud el estiramiento inicial del muelle y de frecuencia: 7

Ejemplo: un objeto de 200 g sujeto al extremo de un muelle elástico de constante: k=320 N·m-1, se estira inicialmente 15 cm. n n n n Frecuencia angular: ω=(k/m)1/2=40 rad/s (no influye lo que se estira) Realiza una oscilación completa cada T=2π/40= 0, 16 s (idem) Su frecuencia es: f=1/T=6, 37 Hz, es decir, realiza 6, 37 vibraciones cada segundo (idem) Ecuación de la posición (en el S. I. ): xt=0, 15·cos 40 t Ecuación de la rapidez (en el S. I. ): vt=-6, 0·sen 40 t Ecuación de la aceleración (en el S. I. ): at=-240·cos 40 t El objeto vibra entre +0, 15 y -0, 15 m, alcanzando una rapidez máxima en el punto medio de ± 6 m/s, y una aceleración máxima en los extremos de ± 240 m/s 2. 8

Si el muelle (constante k) está colgado del techo y se le cuelga un objeto de masa m: 1. Inicialmente el muelle se alargará una distancia “a” hasta llegar al equilibrio con el peso del objeto, de forma que: mg = k·a 2. Si ahora estiramos el muelle una distancia adicional x (en total: x+a), la fuerza resultante sobre el objeto será la que va hacia arriba que ejerce el muelle: k·(x+a), menos la que va hacia abajo: m·g. En total: Fres=k·x+k·a-m·g 3. Teniendo en cuenta la igualdad del punto 1, entonces: Fres=k·x. Podemos considerar el movimiento del objeto ignorando el peso del objeto y el alargamiento inicial del muelle. 9

Generalización de la ecuación del m. a. s. n n n Si un cuerpo está vibrando entre +A y –A, y empezamos a contar el tiempo (t=0) cuando está en A, entonces ya sabemos que: xt=A·cosωt Pero si empezamos a contar el tiempo cuando está en cualquier otra posición (x 0), la ecuación será: xt=A·cos(ωt+φ), de forma que se cumpla: x 0=A·cosφ, o bien: φ=arc cos (x 0/A) φ se mide en radianes, puede ser positivo o negativo, y se llama: fase inicial. Este factor sólo afecta a las condiciones iniciales (x 0, v 0, a 0, F 0) pero no al conjunto del movimiento que seguirá teniendo las mismas características. En general, podemos reconocer un m. a. s por estas ecuaciones: xt=A·cos(ωt+φ), xt=A·sen(ωt+φ) Si el punto intermedio no es 0 sino otro: B, basta sumar ese término a cualquiera de las dos expresiones anteriores. 10