CINEMTICA Movimiento Rectilneo Uniforme MRU Cinemtica Describir el

CINEMÁTICA Movimiento Rectilíneo Uniforme (MRU)

Cinemática Describir el movimiento de cuerpos • ¿Que tipo de movimiento es? • ¿Cómo se mueven? • ¿Hacia donde se mueven? • ¿Con qué velocidad se mueven? • ¿Dónde estaba inicialmente? • ¿Dónde se encuentra al final? • ¿Qué distancia recorre? • ¿Cuál es su desplazamiento? • ¿Cuál es su velocidad media? • ¿Hubo cambio de dirección?

Cinemática Describir el movimiento de cuerpos • ¿Cuando y dónde se detienen? • ¿Cuál fue su aceleración? • ¿Dónde, cuándo y qué velocidad tienen los cuerpos cuando chocan o se cruzan? • ¿Cuándo alcanza su altura máxima? • ¿Cuál es su alcance horizontal? • ¿Con que velocidad y en que dirección pega cuando llega al suelo?

Sistema de Referencia Para describir (Cinemática) el movimiento o causas (Dinámica) del movimiento de cuerpos es IMPORTANTE tener un Sistema de Referencia a partir del cual se hace la descripción o se analizan las fuerzas que actúan sobre un cuerpo. Tales sistemas son: Línea Recta (m. r. u. / m. r. u. a / caída libre) Plano Cartesiano (tiro parabólico / m. c. u. / dinámica) Sistema tridimensional Todo Sistema de Referencia debe contener: Origen Convención de signos Unidades

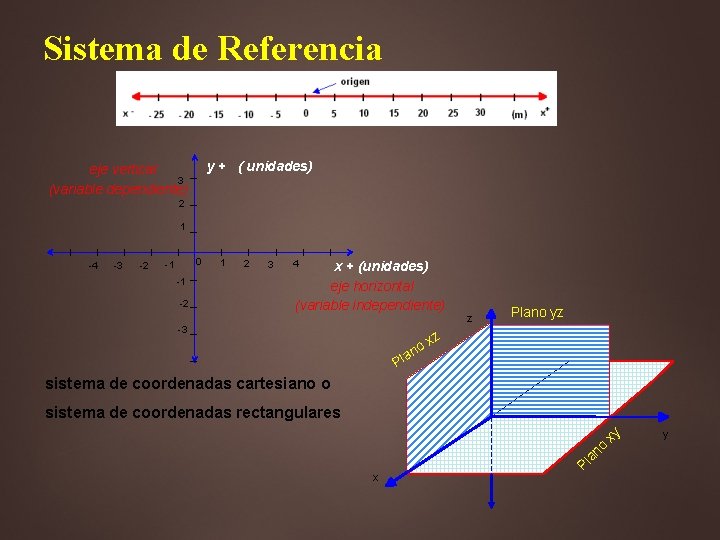
Sistema de Referencia y + ( unidades) 2 1 l l eje vertical 3 (variable dependiente) l l l -1 -2 -3 -4 l l l -1 0 -2 -3 l l l 1 4 2 3 x + (unidades) eje horizontal (variable independiente) z Plano yz z o x n Pla sistema de coordenadas cartesiano o x Pl an o xy sistema de coordenadas rectangulares y

MOVIMIENTO RECILÍNEO MRU Se le denomina movimiento rectilíneo uniforme al movimiento rectilíneo que se desarrolla a velocidad constante, tanto en magnitud, como en dirección y sentido; esto quiere decir que la aceleración es nula (a = 0).

MOVIMIENTOS RECTILÍNEOS Este tipo de movimiento ocurre cuando el móvil se mueve a lo largo de una línea recta; esto quiere decir que es un movimiento unidimensional, o sea, movimiento en una dimensión.

Movimiento Rectilíneo Uniforme • El cuerpo recorre distancias iguales en iguales intervalos de tiempo El desplazamiento o cambio de posición es: Dx = x f - x i Para un desplazamiento particular: Dx = x 3 - x 2 Los intervalos de tiempo son: Dt = t f - t i Donde tf > ti. Por tanto, Siempre ocurre que: Dt > 0 ¡¡¡ No existen tiempos negativos !!! A partir de la observación ( y medir posición y tiempo), se registran los datos en una Tabulación t(s) 0 x (m) 0 2 4 6 8 30 60 90 120

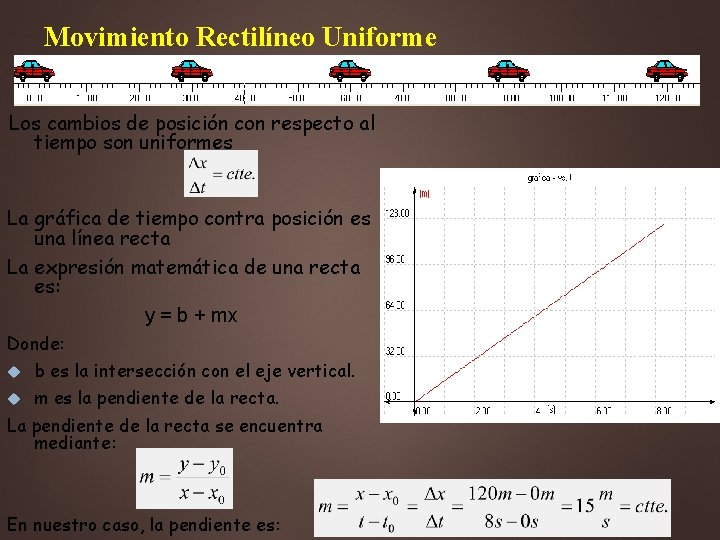
Movimiento Rectilíneo Uniforme Los cambios de posición con respecto al tiempo son uniformes La gráfica de tiempo contra posición es una línea recta La expresión matemática de una recta es: y = b + mx Donde: b es la intersección con el eje vertical. m es la pendiente de la recta. La pendiente de la recta se encuentra mediante: En nuestro caso, la pendiente es:

Movimiento Rectilíneo Uniforme En una gráfica de posición contra tiempo (x vs. t), la pendiente de la recta me da la VELOCIDAD. La ecuación de la recta se encuentra a partir despejar x de la formula para la pendiente x = x 0 + v (t – t 0) También se le conoce como: ECUACIÓN DE MOVIMIENTO RECTILÍNEO UNIFORME (uniforme debido a que la velocidad no cambia, siempre es la misma, es una constante) Donde a la velocidad se le conoce como velocidad media o velocidad uniforme

Luego: (1) Se obtiene: (2) (3) En el caso de que ti = 0, las ecuaciones se simplificarían en. (4)

Esta ecuación representa la posición de un móvil que describe un movimiento rectilíneo uniforme en cualquier instante, respecto a un sistema de referencia determinado. Para el M. R. U. y según el sistema de referencia se tienen gráficos:

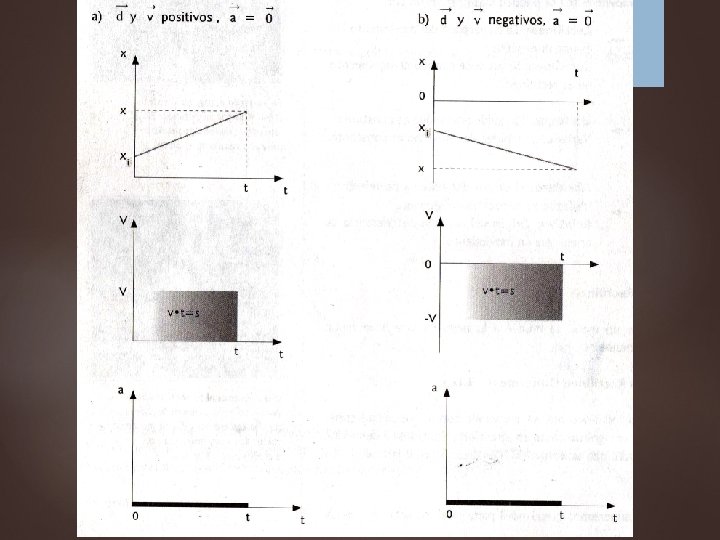
Movimiento Rectilíneo Uniforme En el desplazamiento: Dx = xf – x 0 Si xf > x 0 entonces Dx > 0 (Mov. Derecha) Si xf < x 0 entonces Dx < 0 (Mov. Izquierda) Si xf = x 0 entonces Dx = 0 (Reposo o Regreso) Ejemplos: PLAY Analizar el movimiento ¿Qué valor tiene la velocidad? ¿Qué signo tiene? ¿Significa lo mismo velocidad y rapidez?

Movimiento Rectilíneo Uniforme En una gráfica de x vs. t si la pendiente de la recta es: Positiva, el cuerpo se mueve hacia la derecha. Negativa, el cuerpo se mueve hacia la izquierda. Realice una Gráfica de velocidad contra tiempo (v vs. t) del ejemplo mru derecha. Encuentre el Área del rectángulo y diga que unidades tiene. En función de lo anterior, diga que significa el Área bajo una recta en una gráfica de posición vs. tiempo.

Retroalimentación En el movimiento rectilíneo uniforme la velocidad es una constante. El cuerpo recorre distancias iguales en iguales intervalos de tiempo. El desplazamiento es: Dx = x – x 0 La velocidad media o uniforme es: v = Dx / Dt La ecuación de movimiento rectilíneo uniforme es: x = x 0 + v (t – t 0) La gráfica de la ecuación anterior es una línea recta. En una gráfica de x vs. t la pendiente de la recta me da la velocidad.

Retroalimentación Cuando se da una ecuación de movimiento, en ella está contenida la posición inicial y la velocidad. Para conocerlas, compare la ecuación de ese cuerpo con la ecuación general de mru. x = 100 – 20 t (donde x está en m y t en s) x = x 0 + v t x 0 = 100 m v = -20 m/s Si se pide el tiempo que tarda el cuerpo en llegar al origen del sistema, entonces se sustituye x = 0 ¿Puede describir el movimiento del cuerpo de la ecuación anterior?

Análisis Gráfico Se adopta una convención de signos, la universalmente aceptada es positivos a la derecha y negativos hacia la izquierda para el eje horizontal. Positivos hacia arriba y negativos hacia abajo para el vertical. Las escalas deben ser tales que la gráfica sea proporcional en ambos ejes y que los puntos que en ella marquemos no se encuentren ni muy pegados ni muy distanciados. La escala debe de ser en números enteros. (no marcar puntos intermedios entre los valores convenidos)

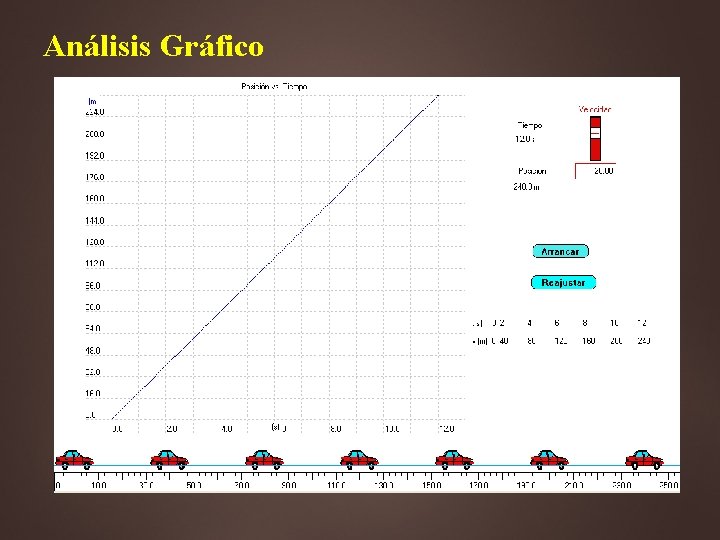
Análisis Gráfico

Análisis Gráfico ¿Es posible aprovechar la regularidad que presenta el auto para conocer sus posiciones en tiempos que no están en la tabla de datos? Por ejemplo: ¿Cuál fue su posición en los tiempos t = 1 s, t = 5 s, t = 10 s? ó bien ¿En qué tiempo la posición del automóvil fue de 50 m? ¿Cuándo paso por la posición 100 m? Realizando el análisis se encuentra que: x = 20 t

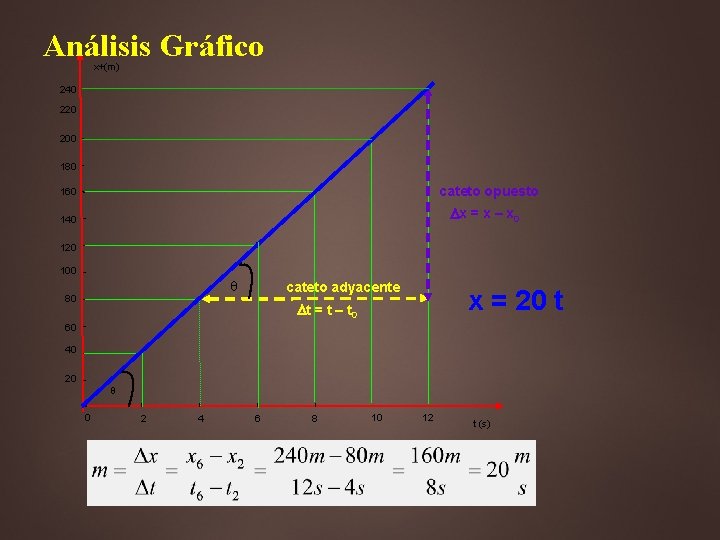
Análisis Gráfico x (m) + 240 220 200 180 cateto opuesto 160 Dx = x – x 0 140 o 120 100 q 80 cateto adyacente o x = 20 t Dt = t – t 0 60 40 o 20 q o l 0 2 l l l 4 6 8 10 12 t (s)

Interpolación Del ejemplo anterior: - Si nos interesa la posición en t = 5. 9 s, la podemos encontrar evaluando en t = 5. 9 s x = 20(m/s)(5. 9 s)=118 m De igual forma si nos interesa la posición el tiempo t = 23. 7 s x = 20(m/s)(23. 7 s)=474 m Además si nos interesa conocer cuanto tiempo le toma alcanzar la posición de 150 m simplemente despejamos t de la ecuación: x = x 0 + v (t – t 0) t = (x – x 0) / v dado que x = 150 m, x 0 = 0 m y v = 20 m/s; entonces t= 7. 5 s

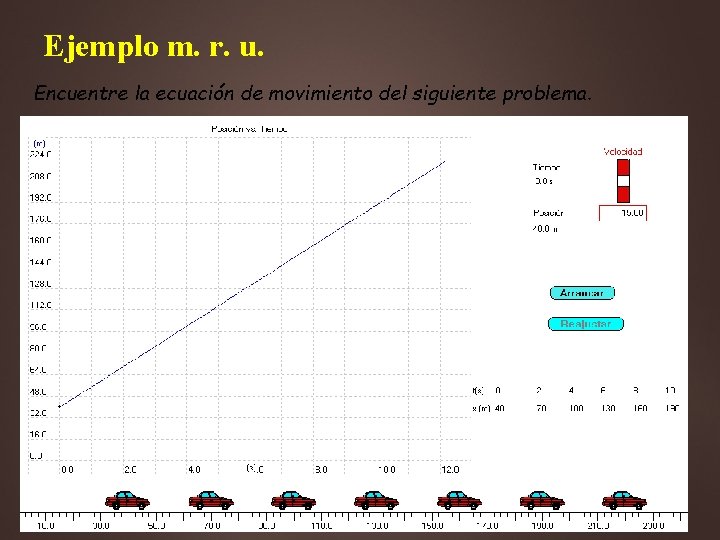
Ejemplo m. r. u. Encuentre la ecuación de movimiento del siguiente problema.

Ejemplo m. r. u. x = 40 + 15 t Describa el movimiento del cuerpo del problema anterior