MOVIMIENTO ARMNICO SIMPLE Qu es el movimiento armnico

MOVIMIENTO ARMÓNICO SIMPLE

¿Qué es el movimiento armónico simple? � Un movimiento armónico simple es un movimiento periódico y oscilatorio, sin rozamiento, producido por una fuerza recuperadora proporcional al desplazamiento y aplicada en la misma dirección pero en sentido contrario. � Son movimientos vibratorios que se pueden expresar mediante funciones armónicas.

Conceptos previos �Movimiento periódico: - Se repite a intervalos iguales de tiempo -Periodo Se mide en segundos T : Tiempo transcurrido entre dos puntos equivalentes de la oscilación (Se deducirá más adelante) -Frecuencia F: número de oscilaciones que se realiza en un segundo Se mide en hertz o

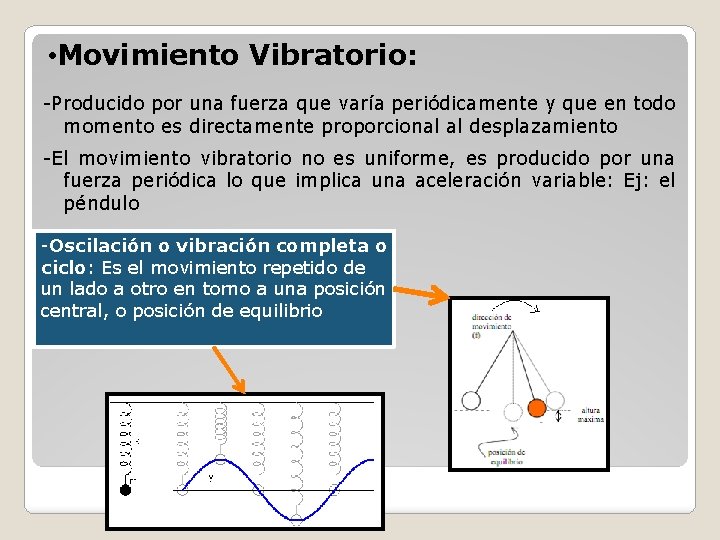
• Movimiento Vibratorio: -Producido por una fuerza que varía periódicamente y que en todo momento es directamente proporcional al desplazamiento -El movimiento vibratorio no es uniforme, es producido por una fuerza periódica lo que implica una aceleración variable: Ej: el péndulo -Oscilación o vibración completa o ciclo: Es el movimiento repetido de un lado a otro en torno a una posición central, o posición de equilibrio

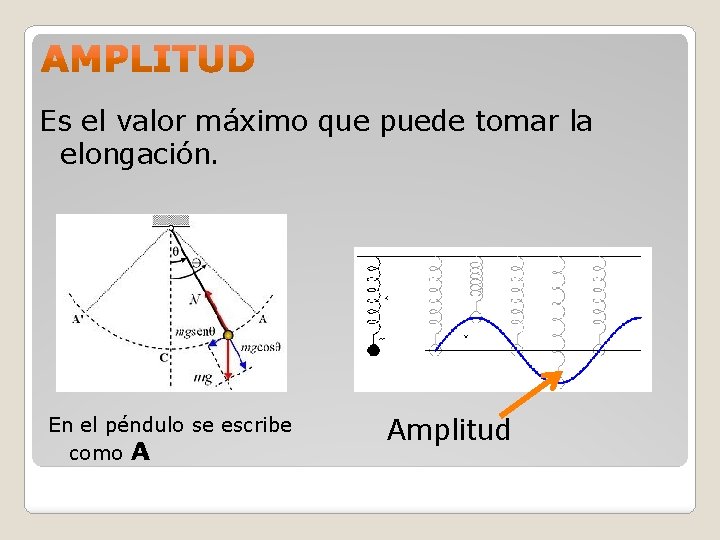
Es el valor máximo que puede tomar la elongación. En el péndulo se escribe como A Amplitud

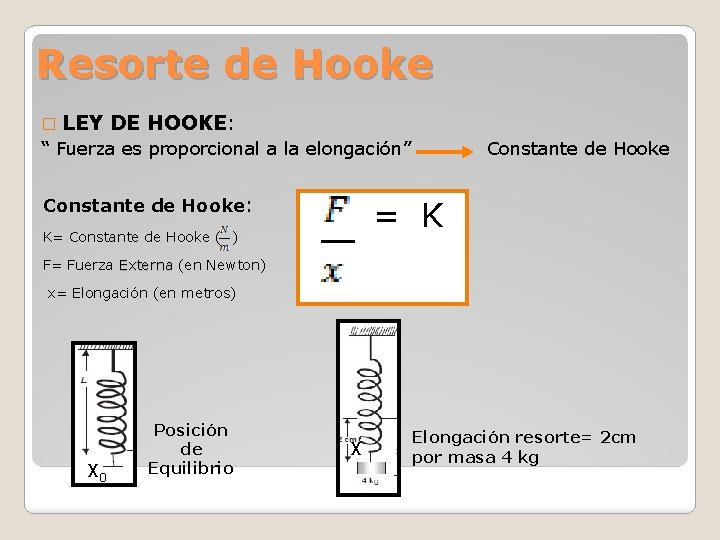
Resorte de Hooke � LEY DE HOOKE: “ Fuerza es proporcional a la elongación” Constante de Hooke: Constante de Hooke = K K= Constante de Hooke ( ) F= Fuerza Externa (en Newton) x= Elongación (en metros) X 0 Posición de Equilibrio X Elongación resorte= 2 cm por masa 4 kg

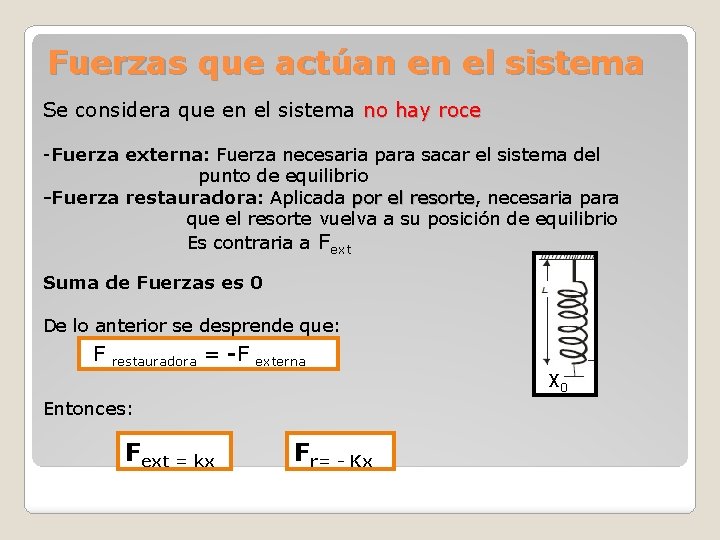
Fuerzas que actúan en el sistema Se considera que en el sistema no hay roce -Fuerza externa: Fuerza necesaria para sacar el sistema del punto de equilibrio -Fuerza restauradora: Aplicada por el resorte, resorte necesaria para que el resorte vuelva a su posición de equilibrio Es contraria a Fext Suma de Fuerzas es 0 De lo anterior se desprende que: F restauradora = -F externa X 0 Entonces: Fext = kx Fr= - Kx

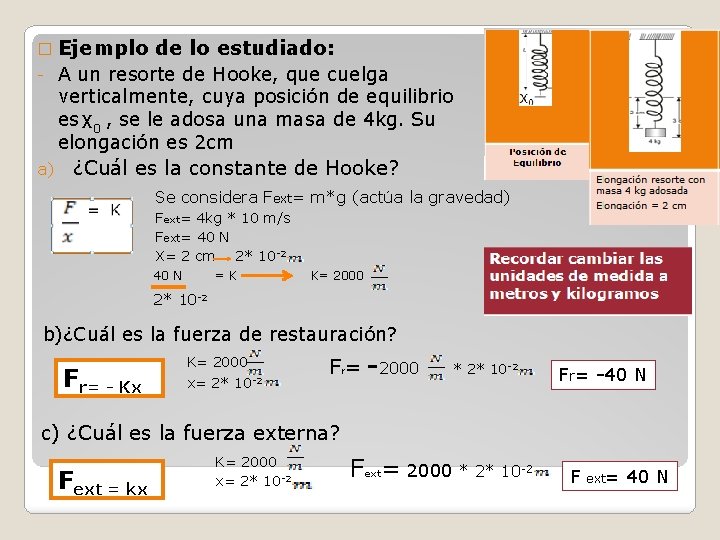
� Ejemplo - a) de lo estudiado: A un resorte de Hooke, que cuelga verticalmente, cuya posición de equilibrio es X 0 , se le adosa una masa de 4 kg. Su elongación es 2 cm ¿Cuál es la constante de Hooke? Se considera Fext= m*g (actúa la gravedad) Fext= 4 kg * 10 m/s Fext= 40 N X= 2 cm 2* 10 -2 40 N =K K= 2000 2* 10 -2 b)¿Cuál es la fuerza de restauración? Fr= - Kx K= 2000 x= 2* 10 -2 Fr= -2000 * 2* 10 -2 Fr= -40 N c) ¿Cuál es la fuerza externa? Fext = kx K= 2000 x= 2* 10 -2 Fext= 2000 * 2* 10 -2 F ext= 40 N

Trabajo � Si la fuerza es constante se tiene que: Método del gráfico 6 4 2 0 1 4 Podemos determinar el trabajo realizado entre las posiciones x 1 y x 2 calculando el área sombreada, es decir: w= Fx x: distancia F: fuerza externa Se deduce la fórmula para M. A. S W= ½ * Kx

Aceleración � Magnitud vectorial que nos indica el cambio de velocidad por unidad de tiempo. Su unidad en el Sistema Internacional es el m/s 2. � En M. A. S es siempre negativa Deducción fórmula: x: elongación cualquiera F= -Kx ma = -Kx k: constante m: masa que mueve el sistema a= -Kx m Se considera que el resorte no tiene masa

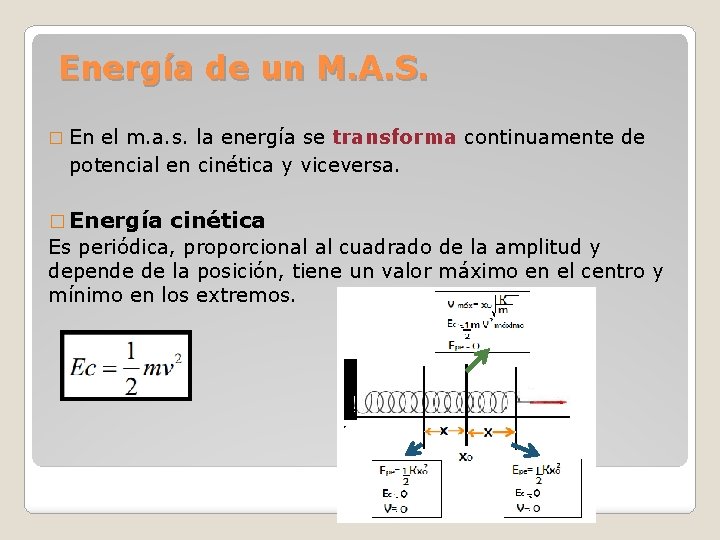
Energía de un M. A. S. � En el m. a. s. la energía se transforma continuamente de potencial en cinética y viceversa. � Energía cinética Es periódica, proporcional al cuadrado de la amplitud y depende de la posición, tiene un valor máximo en el centro y mínimo en los extremos.

� Energía potencial elástica La energía potencial (Ep) almacenada en un resorte estirado o comprimido esta dada por: Energía mecánica No depende de la posición. Es constante

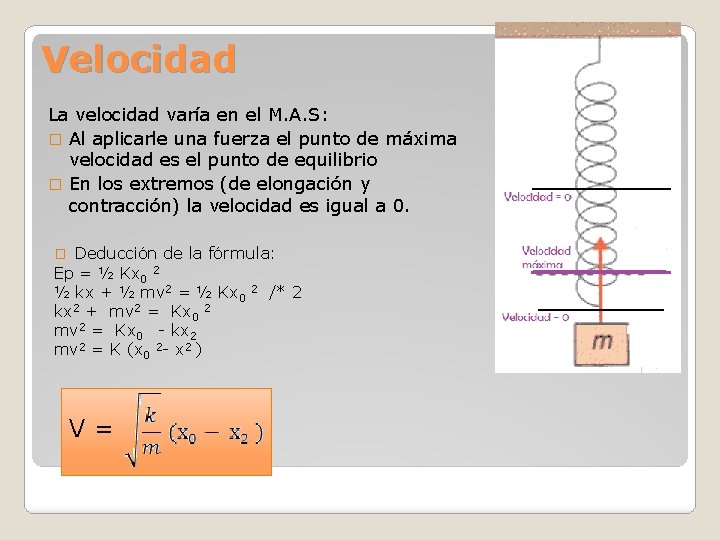
Velocidad La velocidad varía en el M. A. S: � Al aplicarle una fuerza el punto de máxima velocidad es el punto de equilibrio � En los extremos (de elongación y contracción) la velocidad es igual a 0. Deducción de la fórmula: Ep = ½ Kx 0 2 ½ kx + ½ mv 2 = ½ Kx 0 2 /* 2 kx 2 + mv 2 = Kx 0 2 mv 2 = Kx 0 - kx 2 mv 2 = K (x 0 2 - x 2 ) � V=

Periodo • Es el tiempo que tarda el movimiento en repetirse o tiempo que tarda la partícula en realizar una vibración completa � Aplicando las leyes de la dinámica y sabiendo que la aceleración de un movimiento armónico simple es a = - w 2 x (para M. A. S cinemática) tenemos: � Si sustituimos por su valor en función del período y despejamos éste, nos queda:

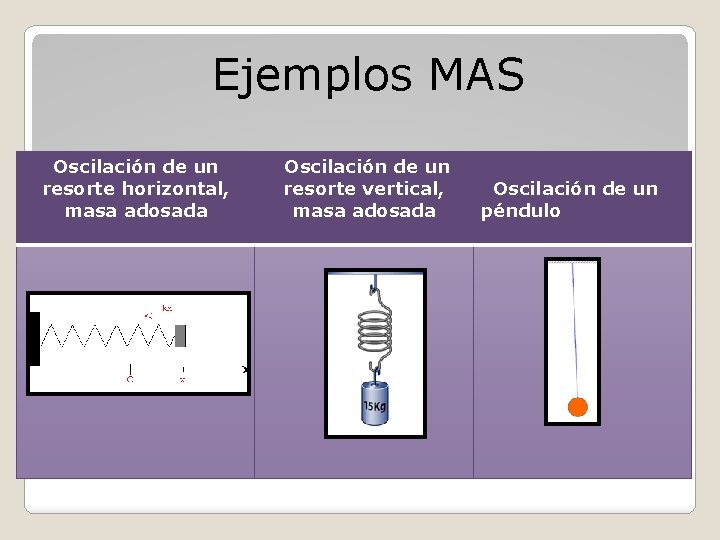
Ejemplos MAS Oscilación de un resorte horizontal, masa adosada Oscilación de un resorte vertical, masa adosada Oscilación de un péndulo

Péndulo � Es un sistema idealizado constituido por una partícula de masa m que está suspendida de un punto fijo o mediante un hilo inextensible y sin peso. � Es imposible la realización práctica de un péndulo simple, pero si es accesible a la teoría.

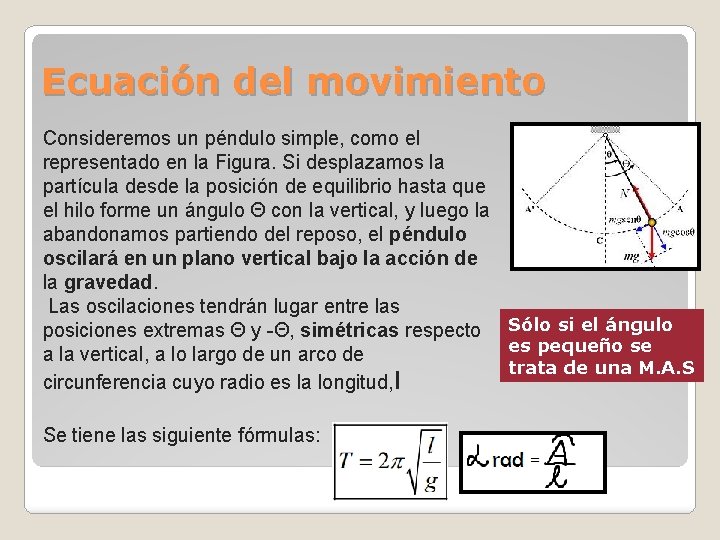
Ecuación del movimiento Consideremos un péndulo simple, como el representado en la Figura. Si desplazamos la partícula desde la posición de equilibrio hasta que el hilo forme un ángulo Θ con la vertical, y luego la abandonamos partiendo del reposo, el péndulo oscilará en un plano vertical bajo la acción de la gravedad. Las oscilaciones tendrán lugar entre las posiciones extremas Θ y -Θ, simétricas respecto Sólo si el ángulo es pequeño se a la vertical, a lo largo de un arco de trata de una M. A. S circunferencia cuyo radio es la longitud, l Se tiene las siguiente fórmulas:

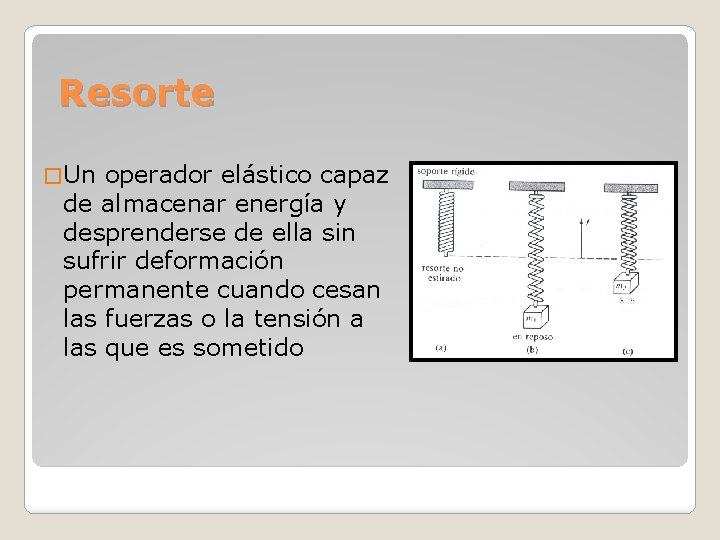
Resorte � Un operador elástico capaz de almacenar energía y desprenderse de ella sin sufrir deformación permanente cuando cesan las fuerzas o la tensión a las que es sometido

Tabla ejemplo resorte con masa adosada