Chapter 29 Electromagnetic Induction and Faradays Law Copyright

Chapter 29 Electromagnetic Induction and Faraday’s Law Copyright © 2009 Pearson Education, Inc.

29 -3 EMF Induced in a Moving Conductor Example 29 -7: Electromagnetic blood-flow measurement. The rate of blood flow in our body’s vessels can be measured using the apparatus shown, since blood contains charged ions. Suppose that the blood vessel is 2. 0 mm in diameter, the magnetic field is 0. 080 T, and the measured emf is 0. 10 m. V. What is the flow velocity of the blood? Remind you of the Hall effect? Copyright © 2009 Pearson Education, Inc.

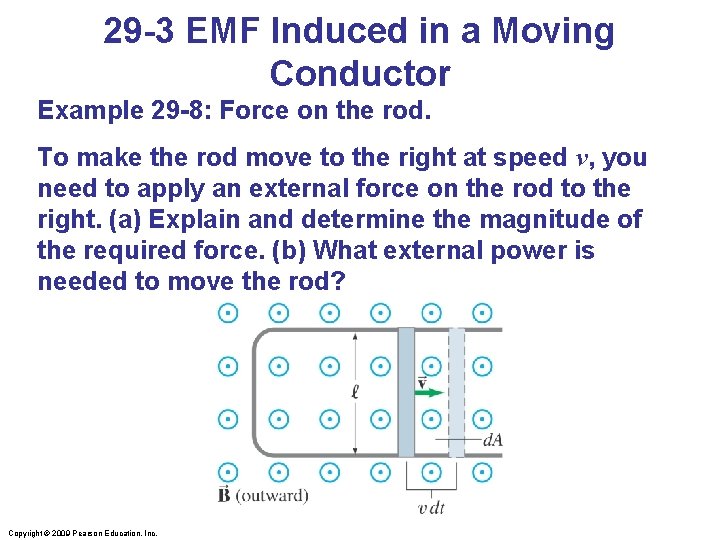
29 -3 EMF Induced in a Moving Conductor Example 29 -8: Force on the rod. To make the rod move to the right at speed v, you need to apply an external force on the rod to the right. (a) Explain and determine the magnitude of the required force. (b) What external power is needed to move the rod? Copyright © 2009 Pearson Education, Inc.

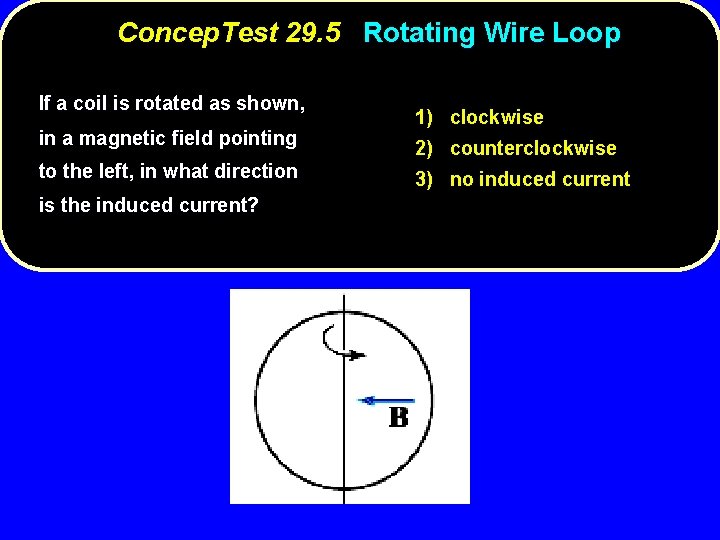
Concep. Test 29. 5 Rotating Wire Loop If a coil is rotated as shown, in a magnetic field pointing to the left, in what direction is the induced current? 1) clockwise 2) counterclockwise 3) no induced current

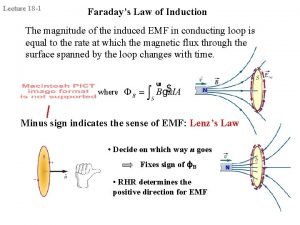
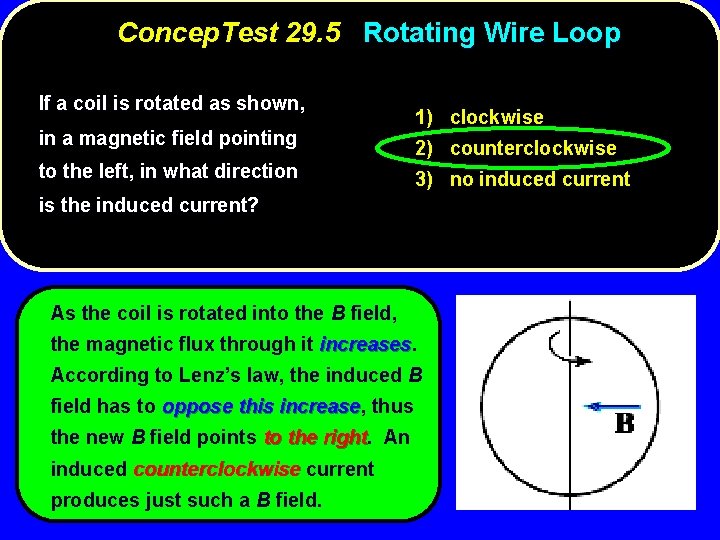
Concep. Test 29. 5 Rotating Wire Loop If a coil is rotated as shown, in a magnetic field pointing to the left, in what direction 1) clockwise 2) counterclockwise 3) no induced current is the induced current? As the coil is rotated into the B field, the magnetic flux through it increases According to Lenz’s law, the induced B field has to oppose this increase, increase thus the new B field points to the right An induced counterclockwise current produces just such a B field.

29 -4 Electric Generators A generator is the opposite of a motor – it transforms mechanical energy into electrical energy. This is an ac generator: The axle is rotated by an external force such as falling water or steam. The brushes are in constant electrical contact with the slip rings. Copyright © 2009 Pearson Education, Inc.

29 -4 Electric Generators If the loop is rotating with constant angular velocity ω, the induced emf is sinusoidal: For a coil of N loops, Copyright © 2009 Pearson Education, Inc.

29 -4 Electric Generators Example 29 -9: An ac generator. The armature of a 60 -Hz ac generator rotates in a 0. 15 -T magnetic field. If the area of the coil is 2. 0 x 10 -2 m 2, how many loops must the coil contain if the peak output is to be V 0 = 170 V? Copyright © 2009 Pearson Education, Inc.

Concep. Test 29. 10 Generators A generator has a coil of wire rotating in a magnetic field. If the rotation rate increases, 1) increases 2) decreases how is the maximum output 3) stays the same voltage of the generator 4) varies sinusoidally affected?

Concep. Test 29. 10 Generators A generator has a coil of wire rotating in a magnetic field. If the rotation rate increases, 1) increases 2) decreases how is the maximum output 3) stays the same voltage of the generator 4) varies sinusoidally affected? The maximum voltage is the leading term that multiplies sin wt and is given by e 0 = NBAw. Therefore, if w increases, increases then e 0 must increase as well.

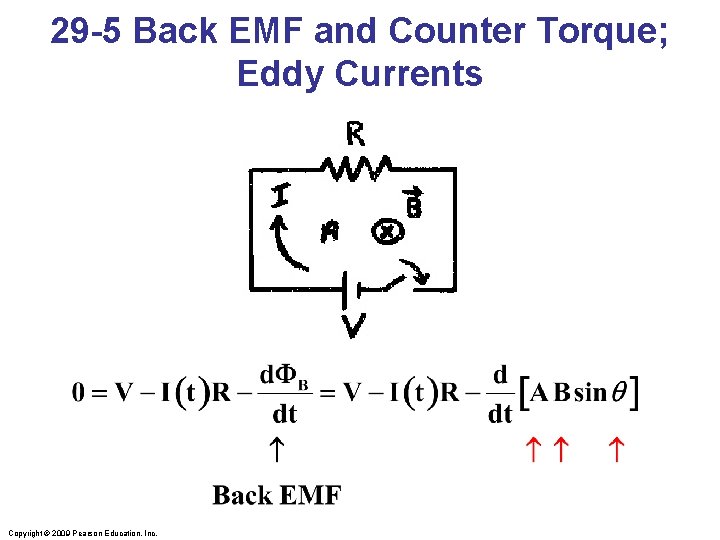
29 -5 Back EMF and Counter Torque; Eddy Currents Copyright © 2009 Pearson Education, Inc.

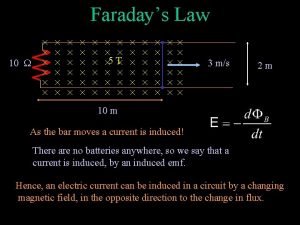
29 -5 Back EMF and Counter Torque; Eddy Currents Induced currents can flow in bulk material as well as through wires. These are called eddy currents, and can dramatically slow a conductor moving into or out of a magnetic field. Copyright © 2009 Pearson Education, Inc.

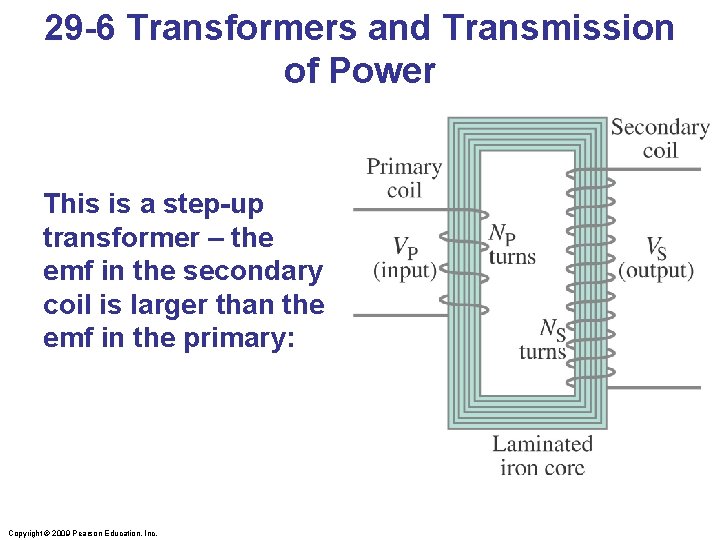
29 -6 Transformers and Transmission of Power A transformer consists of two coils, either interwoven or linked by an iron core. A changing emf in one induces an emf in the other. The ratio of the emfs is equal to the ratio of the number of turns in each coil: Copyright © 2009 Pearson Education, Inc.

29 -6 Transformers and Transmission of Power This is a step-up transformer – the emf in the secondary coil is larger than the emf in the primary: Copyright © 2009 Pearson Education, Inc.

29 -6 Transformers and Transmission of Power Energy must be conserved; therefore, in the absence of losses, the ratio of the currents must be the inverse of the ratio of turns: Copyright © 2009 Pearson Education, Inc.

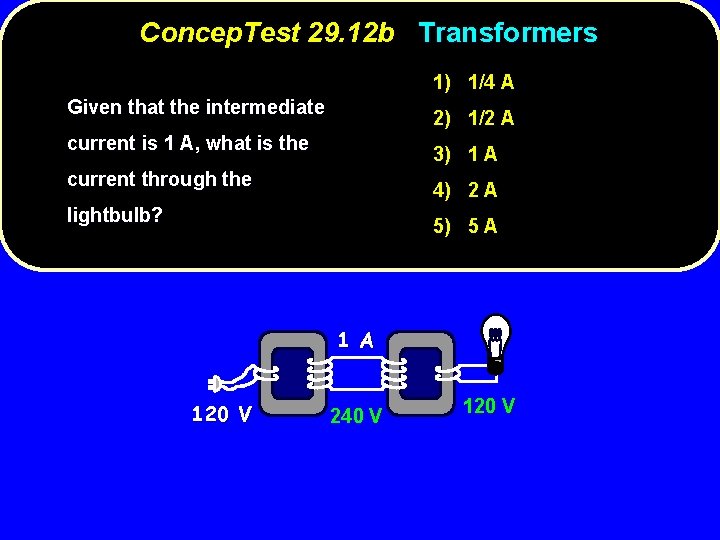
Concep. Test 29. 12 b Transformers 1) 1/4 A Given that the intermediate 2) 1/2 A current is 1 A, what is the 3) 1 A current through the 4) 2 A lightbulb? 5) 5 A 120 V 240 V 120 V

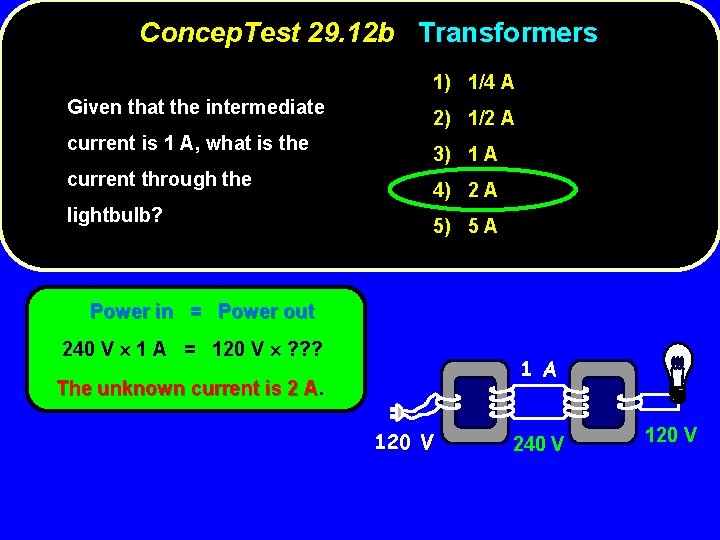
Concep. Test 29. 12 b Transformers 1) 1/4 A Given that the intermediate current is 1 A, what is the current through the lightbulb? 2) 1/2 A 3) 1 A 4) 2 A 5) 5 A Power in = Power out 240 V 1 A = 120 V ? ? ? 1 A The unknown current is 2 A. A 120 V 240 V 120 V

29 -6 Transformers and Transmission of Power Example 29 -12: Cell phone charger. The charger for a cell phone contains a transformer that reduces 120 -V ac to 5. 0 -V ac to charge the 3. 7 -V battery. (It also contains diodes to change the 5. 0 -V ac to 5. 0 -V dc. ) Suppose the secondary coil contains 30 turns and the charger supplies 700 m. A. Calculate (a) the number of turns in the primary coil, (b) the current in the primary, and (c) the power transformed. Copyright © 2009 Pearson Education, Inc.

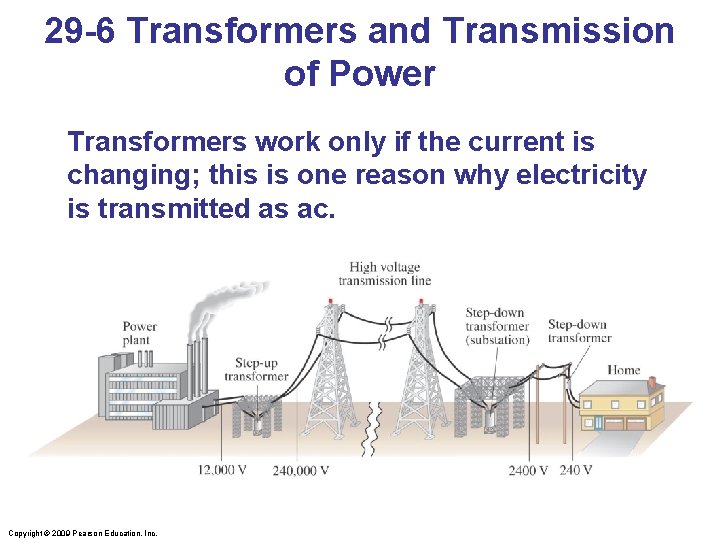
29 -6 Transformers and Transmission of Power Transformers work only if the current is changing; this is one reason why electricity is transmitted as ac. Copyright © 2009 Pearson Education, Inc.

29 -6 Transformers and Transmission of Power Example 29 -13: Transmission lines. An average of 120 k. W of electric power is sent to a small town from a power plant 10 km away. The transmission lines have a total resistance of 0. 40 Ω. Calculate the power loss if the power is transmitted at (a) 240 V and (b) 24, 000 V. Copyright © 2009 Pearson Education, Inc.

29 -7 A Changing Magnetic Flux Produces an Electric Field A changing magnetic flux induces an electric field; this is a generalization of Faraday’s law. The electric field will exist regardless of whethere any conductors around: . Copyright © 2009 Pearson Education, Inc.

29 -7 A Changing Magnetic Flux Produces an Electric Field Example 29 -14: E produced by changing B. A magnetic field B between the pole faces of an electromagnet is nearly uniform at any instant over a circular area of radius r 0. The current in the windings of the electromagnet is increasing in time so that B changes in time at a constant rate d. B/dt at each point. Beyond the circular region (r > r 0), we assume B = 0 at all times. Determine the electric field E at any point P a distance r from the center of the circular area due to the changing B. Copyright © 2009 Pearson Education, Inc.

Summary of Chapter 29 • Magnetic flux: • Changing magnetic flux induces emf: • Induced emf produces current that opposes original flux change. Copyright © 2009 Pearson Education, Inc.

Summary of Chapter 29 • Changing magnetic field produces an electric field. • General form of Faraday’s law: . • Electric generator changes mechanical energy to electrical energy; electric motor does the opposite. Copyright © 2009 Pearson Education, Inc.

Summary of Chapter 29 • Transformer changes magnitude of voltage in ac circuit; ratio of currents is inverse of ratio of voltages: and Copyright © 2009 Pearson Education, Inc.

Chapter 30 Inductance, Electromagnetic Oscillations, and AC Circuits Copyright © 2009 Pearson Education, Inc.

Units of Chapter 30 • Mutual Inductance • Self-Inductance • Energy Stored in a Magnetic Field • LR Circuits • LC Circuits and Electromagnetic Oscillations • LC Circuits with Resistance (LRC Circuits) • AC Circuits with AC Source Copyright © 2009 Pearson Education, Inc.

Units of Chapter 30 • LRC Series AC Circuit • Resonance in AC Circuits • Impedance Matching • Three-Phase AC Copyright © 2009 Pearson Education, Inc.

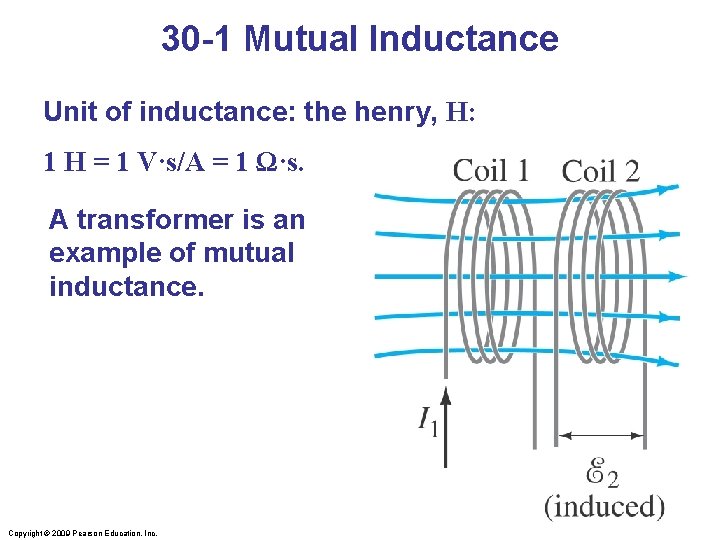
30 -1 Mutual Inductance Mutual inductance: a changing current in one coil will induce a current in a second coil: And vice versa; note that the constant M, known as the mutual inductance, is the same: Copyright © 2009 Pearson Education, Inc.

30 -1 Mutual Inductance Unit of inductance: the henry, H: 1 H = 1 V·s/A = 1 Ω·s. A transformer is an example of mutual inductance. Copyright © 2009 Pearson Education, Inc.

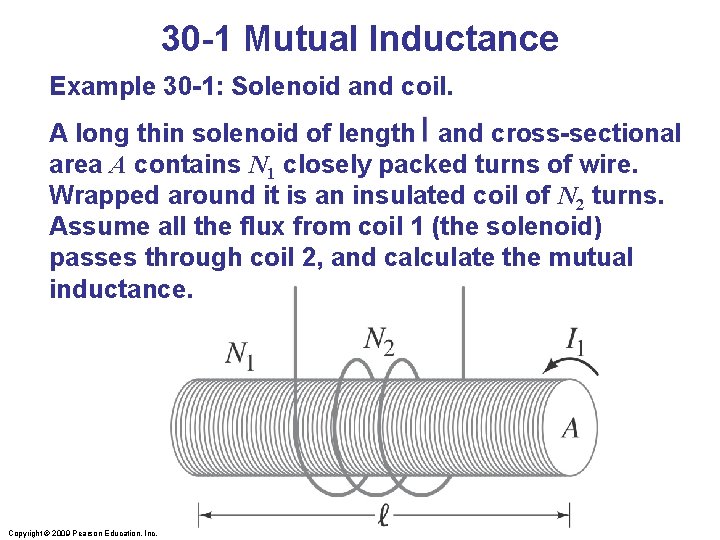
30 -1 Mutual Inductance Example 30 -1: Solenoid and coil. A long thin solenoid of length l and cross-sectional area A contains N 1 closely packed turns of wire. Wrapped around it is an insulated coil of N 2 turns. Assume all the flux from coil 1 (the solenoid) passes through coil 2, and calculate the mutual inductance. Copyright © 2009 Pearson Education, Inc.

30 -2 Self-Inductance A changing current in a coil will also induce an emf in itself: Here, L is called the self-inductance: Copyright © 2009 Pearson Education, Inc.

30 -2 Self-Inductance Example 30 -3: Solenoid inductance. (a) Determine a formula for the self-inductance L of a tightly wrapped and long solenoid containing N turns of wire in its length l and whose cross-sectional area is A. (b) Calculate the value of L if N = 100, l = 5. 0 cm, A = 0. 30 cm 2, and the solenoid is air filled. Copyright © 2009 Pearson Education, Inc.

30 -2 Self-Inductance Conceptual Example 30 -4: Direction of emf in inductor. Current passes through a coil from left to right as shown. (a) If the current is increasing with time, in which direction is the induced emf? (b) If the current is decreasing in time, what then is the direction of the induced emf? Copyright © 2009 Pearson Education, Inc.

30 -3 Energy Stored in a Magnetic Field Just as we saw that energy can be stored in an electric field, energy can be stored in a magnetic field as well, in an inductor, for example. Copyright © 2009 Pearson Education, Inc.