Captulo 03 Cinemtica 1 Introduo A cinemtica o

Capítulo 03: Cinemática 1

Introdução • A cinemática é o ramo da mecânica que lida com quantidades que envolvem somente espaço e tempo. Assim, variáveis como deslocamentos, velocidade, aceleração, deformação e rotação de elementos de fluido sem levar em consideração forças responsáveis pelo movimento são analisadas pela cinemática. • Desse modo, a cinemática descreve essencialmente o aspecto do movimento. 2

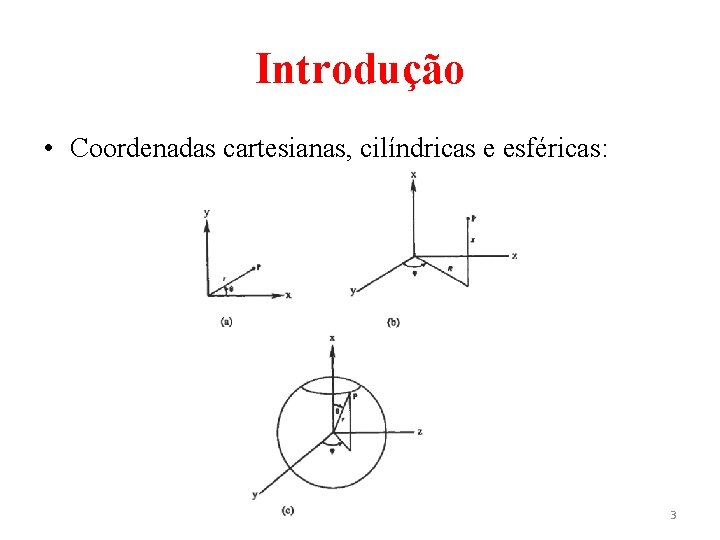
Introdução • Coordenadas cartesianas, cilíndricas e esféricas: 3

Especificações Lagrangianas e Eulerianas • Há duas formas de descrever o movimento de um fluido. Na descrição Lagrangiana, essencialmente segue-se o histórico de partículas individuais de fluido. Consequentemente, toma-se como as duas variáveis independentes o tempo e um rótulo das partículas de fluido. • O rótulo pode ser convenientemente escolhido como o vetor posição a da partícula no tempo de referência t = 0. 4

Especificações Lagrangianas e Eulerianas • Nessa descrição, qualquer variável de escoamento F pode ser expressa como F(a, t). Em particular, o vetor posição é escrito como r = r(a, t), que representa a localização, no tempo t, de uma partícula cuja posição era a em t = 0. 5

Especificações Lagrangianas e Eulerianas • Na descrição Euleriana, o foco está naquilo que ocorre em um ponto específico , de tal modo que as variáveis independentes são e. As variáveis de escoamento são expressas como. • A velocidade e a aceleração de uma partícula de fluido na descrição Lagrangiana são simplesmente derivadas parciais em relação ao tempo: (1) 6

Especificações Lagrangianas e Eulerianas • Isto se deve ao fato de a identidade das partículas se manter constante ao longo da diferenciação. • Observa-se, no entanto, que na descrição Euleriana a derivada parcial fornece apenas a taxa local de variação em um ponto e não a taxa total de variação observada pela partícula de fluido. Termos adicionais são necessários para se avaliar derivadas seguindo uma partícula na descrição Euleriana. 7

Descrições Euleriana e Lagrangiana • A mecânica clássica possui dois tipos de descrição alternativos: a descrição do campo (Euleriana) e a descrição da partícula (Lagrangiana). • Considere qualquer propriedade do fluido em um mesmo instante de tempo e em uma mesma posição nas duas descrições: • Deseja-se, então, expressar 8

Descrições Euleriana e Lagrangiana • Tal expressão corresponde à taxa de variação de F que é observada por uma partícula fixa rotulada pela coordenada a = r(0) em t = 0, nas variáveis de campo. • Como a avaliação é feita para e , que corresponde ao mesmo ponto nas duas descrições, tem-se (2) 9

Descrições Euleriana e Lagrangiana • Ao se diferenciar a expressão anterior, deve-se atentar para se derivar as variáveis dependentes em função das variáveis independentes e, usando a regra da cadeia: (3) • A razão é simplesmente a razão entre as escalas de tempo usadas nas duas descrições. 10

Descrições Euleriana e Lagrangiana • A razão representa a matriz de transformação entre os dois sistemas de coordenadas. Se e r não estão nem rotacionados nem alongados um em relação ao outro, mas sim apresentam eixos paralelos e os comprimentos são expressos na mesma unidade, então • Uma vez que 11

Descrições Euleriana e Lagrangiana • Obtém-se (4) • A taxa total de variação D/Dt é normalmente chamada de derivada material (ou derivada substantiva ou ainda derivada da partícula), enfatizando-se que ela é avaliada seguindo-se um elemento de fluido. 12

Descrições Euleriana e Lagrangiana • A derivada material é composta por duas partes: – A primeira, é a taxa local de variação de F em um dado ponto e é nula para escoamentos em regime permanente. – A segunda, é chamada de derivada advectiva, uma vez que a variação em F resulta na advecção da partícula de uma posição para outra na qual o valor de F é diferente. A advecção corresponde ao movimento do fluido de um local para outro. 13

Descrições Euleriana e Lagrangiana • Em notação vetorial, tem-se (5) • O produto escalar é a magnitude de u multiplicada pela componente de na direção de u. É usual denotar a magnitude do vetor velocidade u por q. Assim, tem-se em notação escalar: (6) 14

Descrições Euleriana e Lagrangiana • Sendo s os pontos ao longo da direção local de u, chamadas de “coordenadas linhas de corrente”. 15

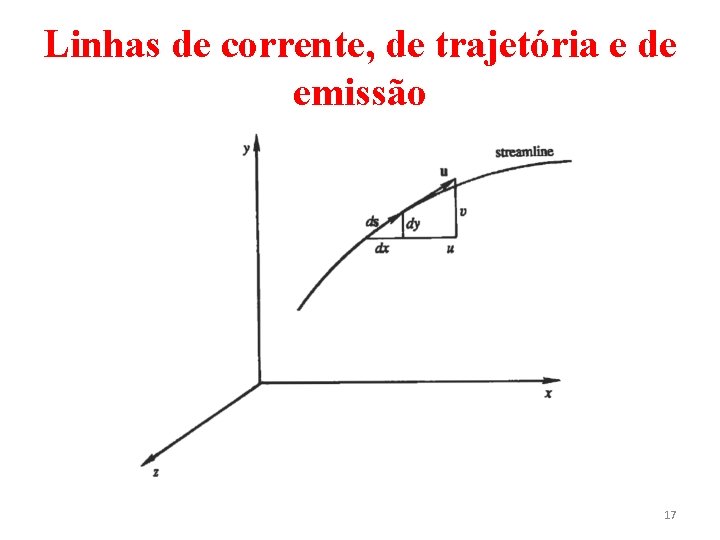
Linhas de corrente, de trajetória e de emissão • Em um instante de tempo, existe em cada ponto de um escoamento um vetor velocidade com uma direção definida. As curvas instantâneas que são tangentes à direção do vetor velocidade em todos os pontos do escoamento são chamadas de linhas de corrente. • Para escoamentos transientes (transitórios), o formato das linhas de corrente muda com o tempo. 16

Linhas de corrente, de trajetória e de emissão 17

Linhas de corrente, de trajetória e de emissão • Seja ds = (dx, dy, dz) um elemento de comprimento de arco ao longo de uma linha de corrente e seja o vetor velocidade local u = (u, v, w). Então, por definição: (7) • ao longo de uma linha de corrente. • Se as componentes da velocidade são funções do tempo conhecidas, pode-se integrar a Eq. (7) para se obter a equação da linha de corrente. 18

Linhas de corrente, de trajetória e de emissão • Pode-se mostrar que a Eq. (7) corresponde a • Todas as linhas de corrente que passam através de uma curva fechada C em um instante de tempo formam um tubo, que é denominado tubo de corrente. 19

Linhas de corrente, de trajetória e de emissão • Fluido não pode atravessar um tubo de corrente pois o vetor velocidade é tangente à sua superfície. • A linha de trajetória é o caminho percorrido por uma partícula de fluido de identidade fixa em um período de tempo. • A linha de trajetória é representada por r = r(a, t), em que a é a localização da partícula em um tempo de referência, por exemplo, t = 0. Então, u = ∂r/∂t para uma partícula fixa. 20

Linhas de corrente, de trajetória e de emissão • Assumindo-se que o determinante do Jacobiano seja não-nulo, pode-se obter a localização da partícula em t = 0, a = a(r, t). • Linhas de trajetória e linhas de corrente são idênticas para escoamentos em regime permanente, mas diferem em escoamentos transientes (transitórios). • As linhas de trajetória são importantes especialmente em experimentos. 21

Linhas de corrente, de trajetória e de emissão • Linhas de corrente e de trajetória para um observador em repouso em relação ao fluido não perturbado: 22

Linhas de corrente, de trajetória e de emissão • Outro conceito importante para a visualização de escoamentos é a de linha de emissão. • A linha de emissão é definida como a localização atual de todas as partículas de fluido que passaram por um ponto fixo no espaço durante um determinado intervalo de tempo. • Experimentalmente, ela pode ser determinada pela injeção de fumaça ou de uma tinta em um dado ponto do escoamento. 23

Referencial e padrão de linhas de corrente • Um escoamento que esteja em regime permanente em um referencial não necessariamente o estará em outro: em (a) observador em repouso em relação ao fluido; em (b) observador sobre o corpo. 24

Taxa de deformação linear • Um estudo da dinâmica dos fluidos envolve a determinação de forças sobre um elemento, a qual depende da natureza e da grandeza das deformações envolvidas. • A deformação de um fluido é similar àquela de um sólido, na qual define-se a deformação linear como a variação no comprimento de um elemento linear por unidade de comprimento e a deformação angular como a variação em relação ao ângulo reto. 25

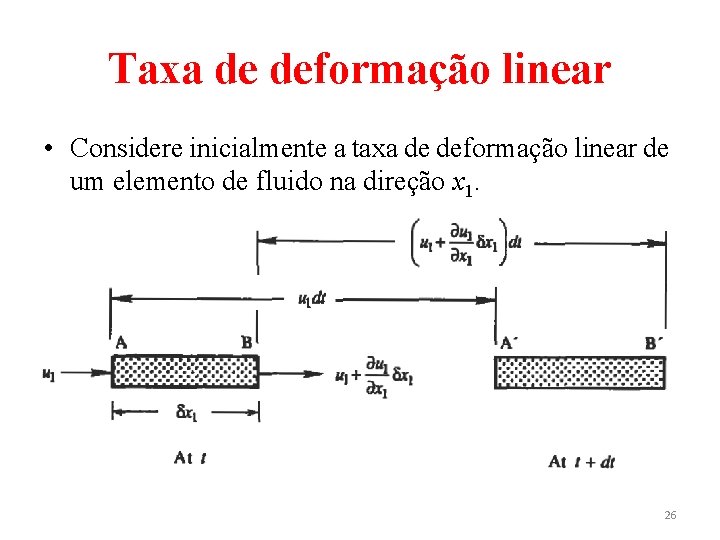
Taxa de deformação linear • Considere inicialmente a taxa de deformação linear de um elemento de fluido na direção x 1. 26

Taxa de deformação linear • A taxa de variação do comprimento por unidade de comprimento é • O símbolo de derivada material D/Dt foi empregado pois implicitamente seguiu-se a partícula de fluido. 27

Taxa de deformação linear • Em geral, a taxa de deformação linear na direção α é (8) • Observa-se que não se deve efetuar a soma sobre o índice repetido α. Letras gregas são normalmente empregadas quando a convenção de soma implícita é violada. 28

Taxa de deformação linear • A soma das taxas de deformação linear em três direções mutuamente ortogonais fornece a taxa de variação de volume por unidade de volume, chamada de taxa de deformação volumétrica. • Considere, então, um elemento de fluido de lados δx 1, δx 2 e δx 3. Definindo-se o volume como 29

Taxa de deformação linear • Tem-se que a taxa de deformação volumétrica é • Ou seja, (9) 30

Taxa de deformação linear • A quantidade ∂ui/∂xi é a soma dos termos da diagonal do tensor gradiente de velocidades ∂ui/∂xj. Como um escalar, ela é invariante em relação à rotação do sistema de coordenadas. • A Eq. (9) será empregada posteriormente para a obtenção da lei da conservação da massa. 31

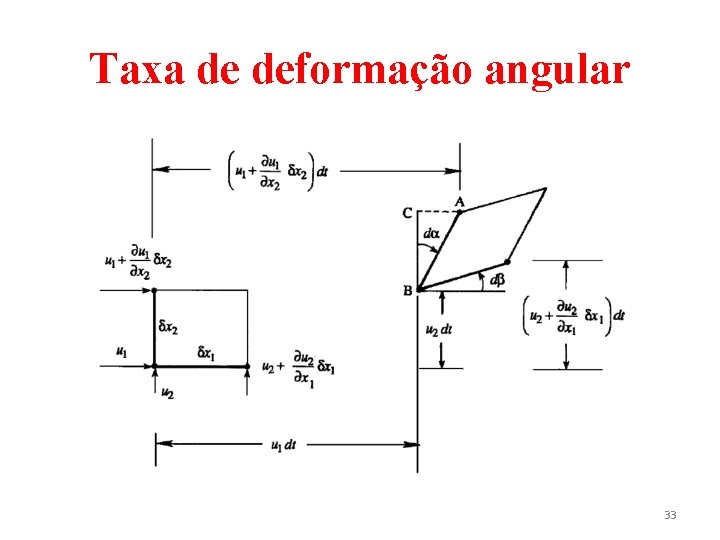
Taxa de deformação angular • Além da deformação linear, um elemento de fluido pode também deformar em seu formato. • A taxa de deformação angular de um elemento é definido como a taxa de redução do ângulo formado por duas linhas mutuamente perpendiculares pertencentes ao elemento. • A deformação angular depende da orientação do par de linhas. 32

Taxa de deformação angular 33

Taxa de deformação angular • Considerando-se a figura anterior, tem-se que a taxa de deformação angular é dada por (10) • Examinando-se as Eqs. (8) e (10), observa-se que a deformação de um elemento de fluido pode ser expressa pelo tensor taxa de deformação. 34

Taxa de deformação angular • Tensor taxa de deformação: (11) • Os elementos da diagonal principal de e são as taxas de deformação lineares dadas pela Eq. (8) e os elementos não-diagonais de e são metade das taxas de deformação angulares dadas pela Eq. (10). Obviamente o tensor taxa de deformação é simétrico. 35

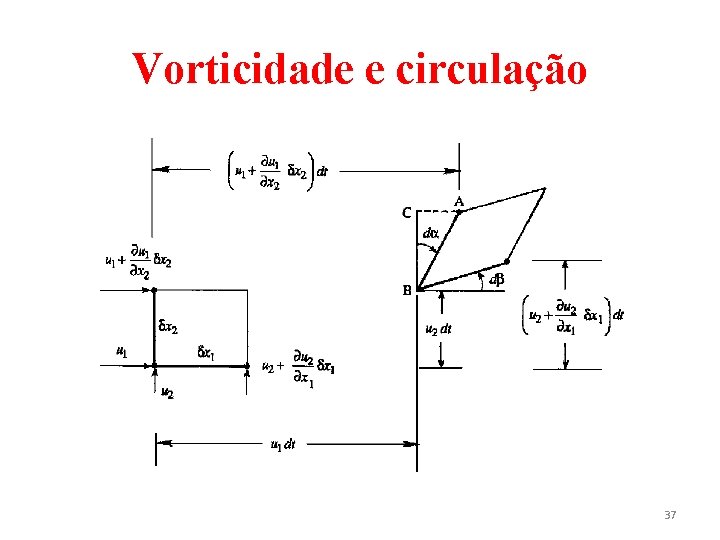
Vorticidade e circulação • Linhas de fluido orientadas ao longo de direções diferentes rotacionam de forma diferente. Para se definir a taxa de rotação de forma clara, duas linhas mutuamente perpendiculares são tomadas e a taxa média de rotação das duas linhas é calculada. Pode-se mostrar que essa média é independente da orientação do par de linhas. • Para evitar o aparecimento de fatores de 2 nas expressões finais, é comum lidar com o dobro da velocidade angular, o que é conhecido como vorticidade do elemento. 36

Vorticidade e circulação 37

Vorticidade e circulação • Considerando-se duas linhas perpendiculares de um elemento de fluido. As velocidades angulares das linhas em relação ao eixo x 3 são dβ/dt e ‒dα/dt, de modo que a média é dada por • A vorticidade do elemento em relação ao eixo x 3 é então duas vezes tal média. 38

Vorticidade e circulação • Desse modo • Da definição do rotacional de um vetor (Eqs. 2. 24 e 2. 25), segue-se que a vorticidade de um elemento de fluido está relacionado com o vetor velocidade. 39

Vorticidade e circulação • Assim: (12) • cujas componentes são: (13) • O movimento de um fluido é chamado de irrotacional se ω = 0. 40

Vorticidade e circulação • Nesse caso, tem-se (14) • Em escoamentos irrotacionais, o vetor velocidade pode ser expresso como o gradiente de uma função escalar ϕ(x, t). Isto se deve ao fato de que (15) • satisfaz à condição de irrotacionalidade. 41

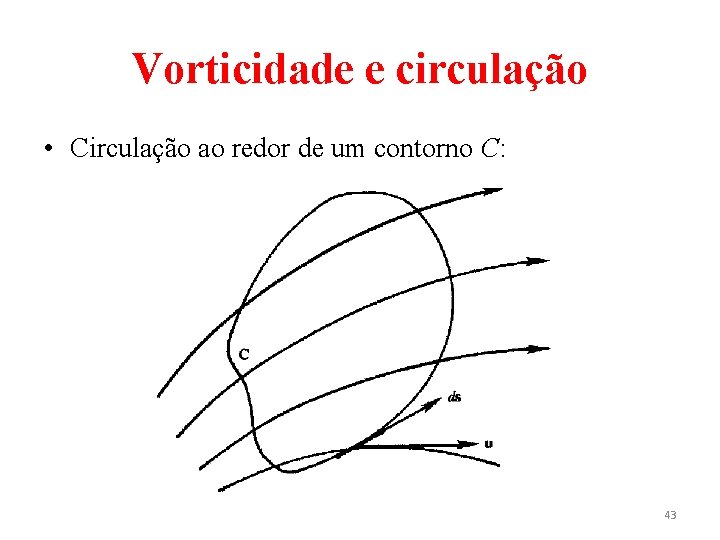
Vorticidade e circulação • Relacionado ao conceito de vorticidade, tem-se o conceito de circulação. A circulação Γ ao redor de uma curva fechada C é definida como a integral de linha da componente tangencial da velocidade e é dada por (16) • onde ds é um elemento de contorno. 42

Vorticidade e circulação • Circulação ao redor de um contorno C: 43

Vorticidade e circulação • O Teorema de Stokes estabelece que (17) • Ou seja, a integral de linha de u ao redor de uma curva fechada C é igual ao “fluxo” de rotacional de u através de uma superfície arbitrária A que é delimitada por C. 44

Vorticidade e circulação • Utilizando a definição de vorticidade e de circulação, tem-se que (18) • Assim, a circulação ao redor de uma curva fechada é igual à integral de superfície da vorticidade, o que é chamada de fluxo de vorticidade. De modo equivalente, a vorticidade em um ponto é igual à circulação por unidade de área. 45

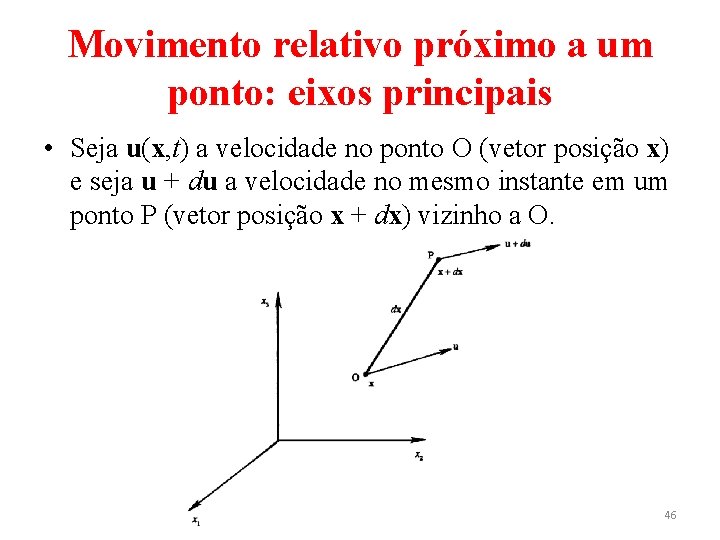
Movimento relativo próximo a um ponto: eixos principais • Seja u(x, t) a velocidade no ponto O (vetor posição x) e seja u + du a velocidade no mesmo instante em um ponto P (vetor posição x + dx) vizinho a O. 46

Movimento relativo próximo a um ponto: eixos principais • A velocidade relativa no instante t é dada por (19) • que fornece três relações do tipo (20) • O termo ∂ui/∂xj na Eq. (19) é o tensor gradiente de velocidades. 47

Movimento relativo próximo a um ponto: eixos principais • Tal tensor pode ser decomposto em uma parte simétrica e uma antissimétrica (21) • que pode ser reescrito como: (22) 48

Movimento relativo próximo a um ponto: eixos principais • Sendo eij o tensor taxa de deformação definido pela Eq. (11) e (23) • é chamado de tensor de rotação. Como rij é antissimétrico, os termos de sua diagonal principal são nulos e os demais termos são de igual magnitude mas opostos. Assim, existem apenas três elementos independentes, r 13, r 21 e r 32. 49

Movimento relativo próximo a um ponto: eixos principais • Comparando-se as Eqs. (13) e (23), observa-se que o tensor de rotação pode ser escrito em termos dos componentes do vetor vorticidade como (24) • O tensor de rotação pode ser escrito em termos do vetor vorticidade como (25) 50

Movimento relativo próximo a um ponto: eixos principais • Substituindo-se as Eqs. (22) e (25) na Eq. (19), obtém -se • que pode ser escrita como (26) 51

Movimento relativo próximo a um ponto: eixos principais • O significado do segundo termo da Eq. (26) é evidente. Sabe-se que a velocidade a uma distância x do eixo de rotação de um corpo rígido rotacionando a uma velocidade Ω é Ω×x. O segundo termo da Eq. (26) representa então a velocidade relativa no ponto P devida à rotação do elemento a uma velocidade angular ω/2. • O primeiro termo da Eq. (26) é a velocidade relativa devida somente à deformação do elemento. 52

Movimento relativo próximo a um ponto: eixos principais • A deformação torna-se particularmente simples para um sistema de coordenadas coincidente com os eixos principais do tensor taxa de deformação. Os componentes de e variam quando o sistema de coordenadas é rotacionado. • Para uma orientação do sistema de coordenadas em particular, um tensor simétrico terá apenas componentes em sua diagonal principal. Tais elementos são chamados de eixos principais do tensor. 53

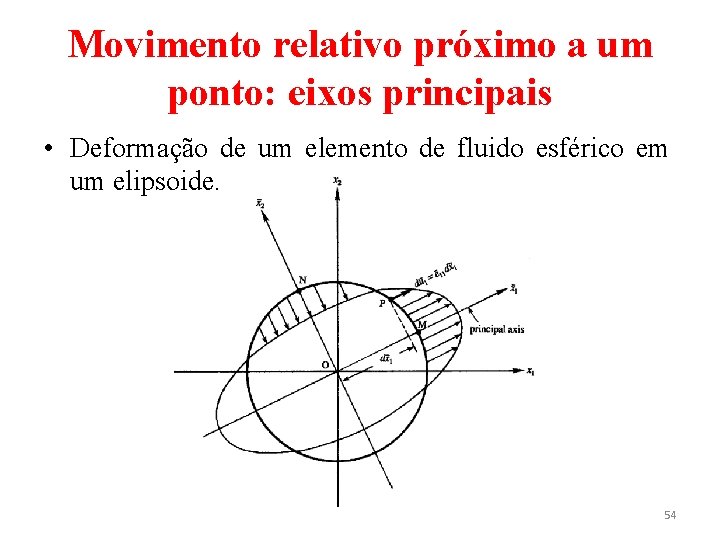
Movimento relativo próximo a um ponto: eixos principais • Deformação de um elemento de fluido esférico em um elipsoide. 54

Movimento relativo próximo a um ponto: eixos principais • Denotando as variáveis no sistema de coordenadas principal, a primeira parte da Eq. (26) pode ser escrita como o produto matricial (27) • Os componentes da diagonal principal de e (. ) são os autovalores de e. , e 55

Movimento relativo próximo a um ponto: eixos principais • Os três componentes da Eq. (27) são (28) • Avaliando-se a parte da Eq. (28), tem-se que se é positiva, tem-se que o ponto P está se movendo para longe de O na direção a uma taxa proporcional à distância. • Considerando-se todos os pontos na superfície de uma esfera, então o movimento de P na direção é máximo quando P coincide com M. 56

Movimento relativo próximo a um ponto: eixos principais • Por sua vez, o movimento de P na direção é mínimo quando P coincide com N. Assim, para um intervalo de tempo pequeno, um elemento de fluido esférico ao redor de O torna-se um elipsoide cujos eixos coincidem com os eixos principais do tensor de deformação e. 57

Movimento relativo próximo a um ponto: eixos principais • Resumo: – A velocidade relativa na vizinhança de um ponto pode ser dividida em duas partes: uma relativa à velocidade angular do elemento e a outra devido à sua deformação. – Um elemento esférico deforma-se em um elipsoide, cujos eixos coincidem com as direções principais do tensor taxa de deformação local. 58

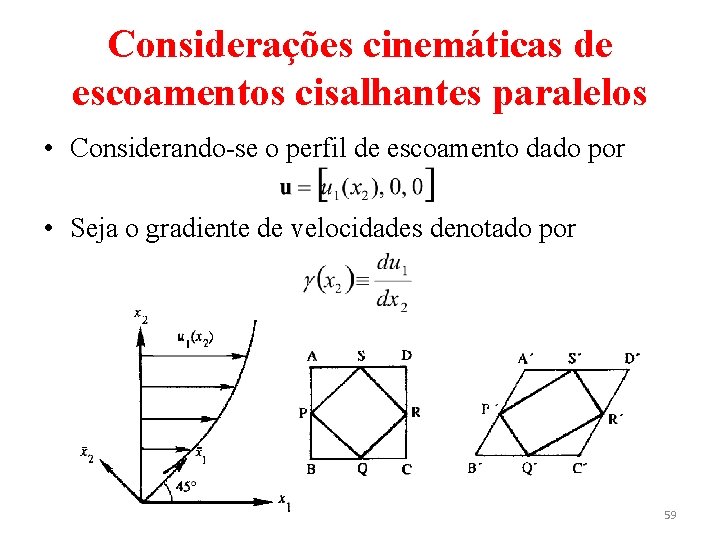
Considerações cinemáticas de escoamentos cisalhantes paralelos • Considerando-se o perfil de escoamento dado por • Seja o gradiente de velocidades denotado por 59

Considerações cinemáticas de escoamentos cisalhantes paralelos • Da Eq. (13), o único componente não-nulo da vorticidade é ω3 = −γ. Para o elemento ABCD, tem-se que a velocidade angular do elemento de linha AB é −γ, enquanto a velocidade angular para BC é nula, resultando um valor de −γ/2 para a velocidade angular média. • O valor médio é independente de quais dois elementos mutuamente perpendiculares no plano x 1 x 2 são escolhidos. 60

Considerações cinemáticas de escoamentos cisalhantes paralelos • Em contraste, os componentes da taxa de deformação dependem da orientação do elemento. Da Eq. (11), o tensor taxa de deformação de um elemento como ABCD com lados paralelos aos eixos x 1 x 2 é • que mostra que existem apenas elementos não-nulos fora da diagonal principal de e. 61

Considerações cinemáticas de escoamentos cisalhantes paralelos • Assim, o elemento ABCD se deformará angularmente mas não linearmente. • Como visto no Cap. 2, um tensor simétrico com diagonal principal nula pode ser diagonalizado pela rotação do sistema de coordenadas em 45°. Assim, ao longo dos eixos principais, o tensor taxa de deformação é 62

Considerações cinemáticas de escoamentos cisalhantes paralelos • Assim, há uma taxa de alongamento de , uma taxa de compressão linear de e nenhum cisalhamento. • Isso pode ser entendido fisicamente examinando-se a deformação de um elemento PQRS orientado a 45°, que se deforma em. Observa-se que o lado PS se alonga enquanto PQ se contrai, enquanto os ângulos entre os lados do elemento permanecem em 90°. 63

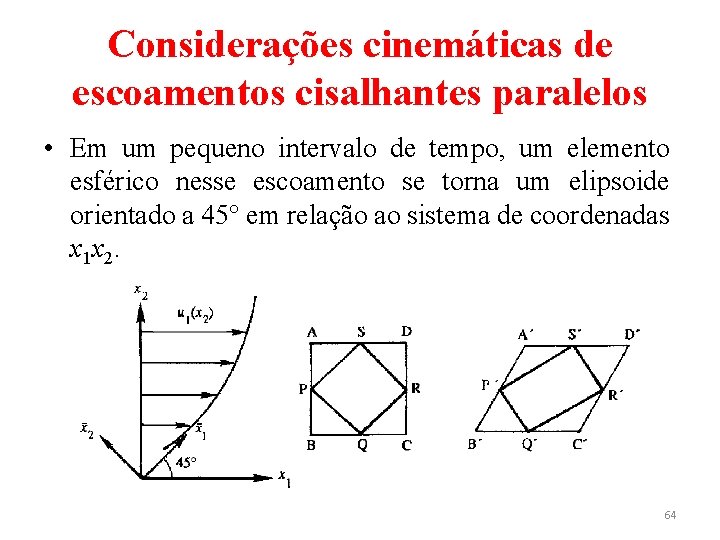
Considerações cinemáticas de escoamentos cisalhantes paralelos • Em um pequeno intervalo de tempo, um elemento esférico nesse escoamento se torna um elipsoide orientado a 45° em relação ao sistema de coordenadas x 1 x 2. 64

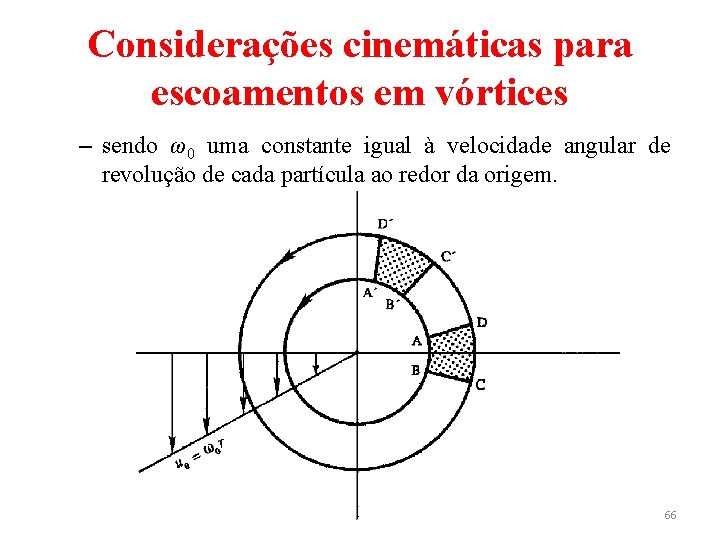
Considerações cinemáticas para escoamentos em vórtices • Escoamentos em caminhos circulares são chamados escoamentos em vórtices e alguns de seus tipos básicos são descritos a seguir. • Rotação de corpo rígido – Considere primeiramente o caso no qual a velocidade é proporcional ao raio das linhas de corrente. Tal escoamento pode ser gerado ao rotacionar um tanque cilíndrico, em regime permanente, contendo um fluido viscoso. Usando coordenadas polares (r, θ) tem-se (29) 65

Considerações cinemáticas para escoamentos em vórtices – sendo ω0 uma constante igual à velocidade angular de revolução de cada partícula ao redor da origem. 66

Considerações cinemáticas para escoamentos em vórtices – Tem-se também que ω0 é igual à velocidade angular de rotação de cada partícula ao redor de seu próprio centro. A componente da vorticidade em relação ao eixo z é: (30) – Esse resultado mostra que a velocidade angular de cada elemento de fluido ao redor de seu próprio centro é uma constante e igual a ω0. – Isto se torna evidente ao se acompanhar a localização de um elemento de fluido ABCD em dois instantes distintos. 67

Considerações cinemáticas para escoamentos em vórtices – Pode-se notar que duas linhas mutuamente perpendiculares AD e AB rotacionam em sentido anti-horário (em relação ao centro do elemento) com velocidade ω0. O período de rotação da partícula em relação ao seu centro é igual ao período de revolução ao redor da origem. – É claro também que a deformação dos elementos de fluido em escoamento é nula, ou seja, cada partícula de fluido mantém sua posição relativa às demais partículas. – Um escoamento definido por uθ = ω0 r é chamado de rotação de corpo rígido pois as partículas de fluido rotacionam como um sólido rígido em rotação. 68

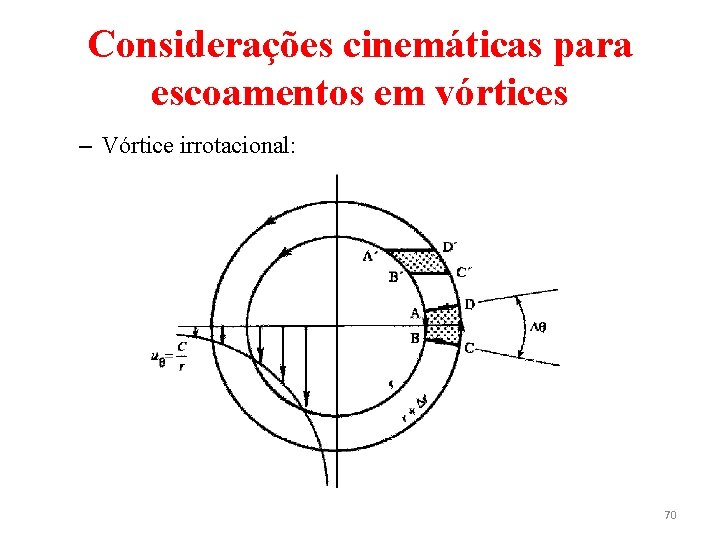
Considerações cinemáticas para escoamentos em vórtices – A circulação ao redor de um circuito de raio r é (31) – Assim, a circulação é igual à vorticidade 2 ω0 multiplicada pela área. • Vórtice irrotacional – Linhas de corrente circulares, no entanto, não implicam que um escoamento tenha vorticidade em todos os pontos. 69

Considerações cinemáticas para escoamentos em vórtices – Vórtice irrotacional: 70

Considerações cinemáticas para escoamentos em vórtices – Considere um escoamento ao redor de caminhos circulares na qual o vetor velocidade é tangencial e inversamente proporcional ao raio da linha de corrente, ou seja, (32) – Usando a Eq. (30), verifica-se que a vorticidade em qualquer ponto do escoamento é – Assim, a vorticidade é nula em todos os pontos, exceto na origem, onde não pode ser determinada por essa expressão. 71

Considerações cinemáticas para escoamentos em vórtices – A vorticidade na origem pode ser determinada considerando-se a circulação ao redor de um circuito fechado que contenha a origem. Ao redor de um contorno de raio r, a circulação é – Esse resultado mostra que Γ é constante, independente do raio, diferentemente do que ocorre no escoamento de corpo rígido. 72

Considerações cinemáticas para escoamentos em vórtices – Considerando-se, então, a implicação do Teorema de Stokes: (33) – para um contorno que contenha a origem. O lado esquerdo da Eq. (33) é não-nulo, o que implica em ω não-nulo em algum ponto dentro da área delimitada pelo contorno. – Como neste escoamento Γ é independente de r, pode-se colapsar o contorno não se alterando o valor do lado esquerdo da Eq. (33). 73

Considerações cinemáticas para escoamentos em vórtices – No limite em que a área se aproxima de zero, deve-se então ter um limite não-nulo na origem. Assim, a vorticidade na origem deve tender ao infinito de modo que tenha um limite finito não-nulo na origem. – Assim, o escoamento representado por uθ = C/r é irrotacional em todos os pontos, exceto na origem, onde a vorticidade é infinita. – Tal escoamento é chamado de irrotacional ou vórtice potencial. 74

Considerações cinemáticas para escoamentos em vórtices – Embora em um escoamento irrotacional a circulação ao redor de um circuito contendo a origem seja não-nula, ao se considerar um circuito não contendo a origem possui circulação nula. – A circulação ao redor de um contorno qualquer ABCD é – Como as integrais de linha de são nulas, tem-se ao redor de BC e DA 75

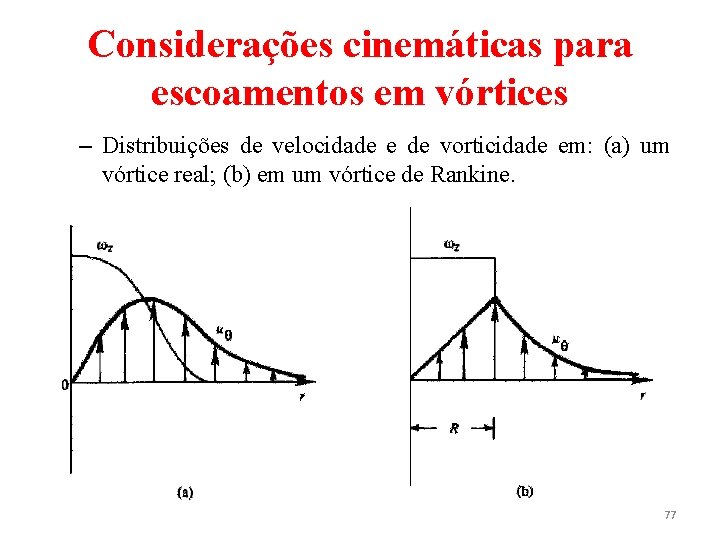
Considerações cinemáticas para escoamentos em vórtices – Nota-se que a integral de linha ao longo de AB é negativa pois u e ds são diretamente opostas e uθ = const. Uma circulação nula ao redor de ABCD é esperada pelo Teorema de Stokes e pelo fato de que a vorticidade desaparece em todos os pontos no interior de ABCD. • Vórtice de Rankine – Vórtices reais, como o vórtice de um ralo ou o de um ciclone atmosférico, possuem um núcleo que rotaciona de modo semelhante à rotação de um corpo rígido e uma região aproximadamente irrotacional a uma certa distância do centro do escoamento. 76

Considerações cinemáticas para escoamentos em vórtices – Distribuições de velocidade e de vorticidade em: (a) um vórtice real; (b) em um vórtice de Rankine. 77

Considerações cinemáticas para escoamentos em vórtices – Um núcleo rotacional deve existir pois a velocidade tangencial em um vórtice irrotacional possui um salto para um valor infinito na origem. – Uma idealização de tal comportamento é chamada de vórtice de Rankine, na qual a vorticidade é considerada uniforme dentro de um núcleo de raio R e é nula exteriormente ao núcleo. 78

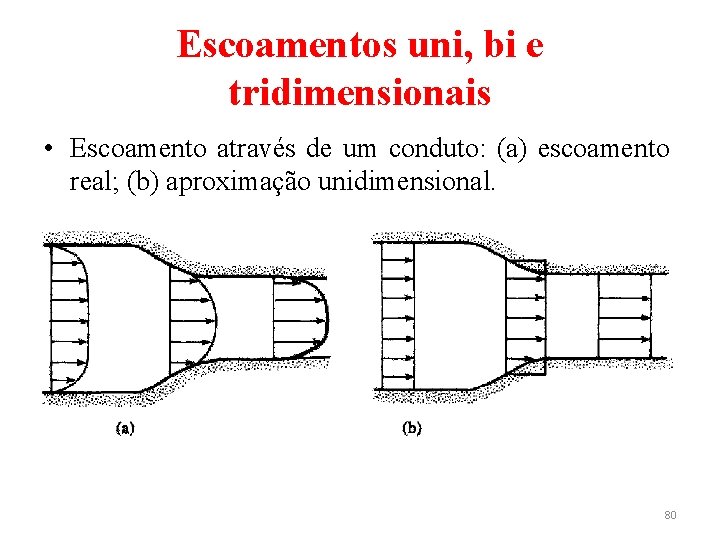
Escoamentos uni, bi e tridimensionais • Escoamentos verdadeiramente unidimensionais são aqueles em que todas as características do escoamento variam apenas em uma direção. • Poucos escoamentos reais são estritamente unidimensionais; muitas vezes, porém, pode-se realizar aproximações para escoamentos unidimensionais, quando o interesse recai em efeitos gerais em uma seção transversal. 79

Escoamentos uni, bi e tridimensionais • Escoamento através de um conduto: (a) escoamento real; (b) aproximação unidimensional. 80

Escoamentos uni, bi e tridimensionais • Um escoamento bidimensional ou plano é aquele em que a variação das características do escoamento ocorrem em apenas duas direções cartesianas. O escoamento sobre um cilindro de seção arbitrária e comprimento infinito é um exemplo de escoamento plano. • Para o escoamento ao redor de corpos de revolução, as variáveis são idênticas em planos contendo o eixo do corpo. 81

Escoamentos uni, bi e tridimensionais • Ao usar coordenadas cilíndricas (R, ϕ, x) com x ao longo do eixo do corpo, somente duas coordenadas (R e x) são necessárias para descrever o movimento. • O escoamento, nesse caso, pode ser chamado de bidimensional (embora não plano). No entanto, normalmente esse tipo de escoamento é descrito como tridimensional axissimétrico. 82

Função de corrente • A descrição de escoamentos incompressíveis bidimensionais pode ser consideravelmente simplificada definindo-se uma função que satisfaça a lei de conservação da massa para tal escoamento. • Embora a obtenção das leis de conservação será apresentada posteriormente, uma forma simples e alternativa da obtenção da lei de conservação da massa será apresentada na sequência. 83

Função de corrente • Partindo-se da taxa de deformação volumétrica dada pela Eq. (9): • A derivada D/Dt significa que acompanha-se uma partícula específica de fluido; observa-se também que o volume de uma partícula é inversamente proporcional à densidade, ou seja, 84

Função de corrente • Obtém-se, desse modo, (34) • A massa específica das partículas não se altera de modo considerável ao longo de seu caminho, sob certas condições, entre as quais a mais importante é a de que a velocidade do escoamento seja pequena quando comparada à velocidade do som no meio. Esta é a chamada aproximação de Boussinesq. 85

Função de corrente • Tal condição é válida para a maioria dos escoamentos de líquidos e vale para escoamentos de gases em que as velocidades são inferiores a aproximadamente 100 m/s. Nesses escoamentos, é muito menor que as derivadas em ∂ui/∂xi, de modo que nesses casos a equação da conservação da massa torna-se 86

Função de corrente • Em muitos casos, a equação da conservação da massa consiste apenas de dois termos: (35) • Isto ocorre quando w não é função de z. Um escoamento plano com w = 0 é o exemplo mais comum de tais escoamentos bidimensionais. Se uma função é definida tal que (36) 87

Função de corrente • Tem-se que a Eq. (35) é automaticamente satisfeita. Assim, uma função de corrente ψ pode ser definida quando a Eq. (35) for válida. • As linhas de corrente do escoamento são dadas por (37) • A substituição da Eq. (36) na Eq. (37) mostra que 88

Função de corrente • Assim, dψ = 0 ao longo de uma linha de corrente. As linhas de corrente instantâneas em um escoamento são dadas por curvas ψ = const. ; cada valor de constante fornece uma linha de corrente diferente. 89

Função de corrente • Considerando-se um elemento de linha arbitrário no escoamento, dx = (dx, dy). Sejam dx e dy positivos. Nesse caso, a vazão volumétrica através de tal elemento de linha é dado por • que mostra que a vazão volumétrica entre um par de linhas de corrente é numericamente igual à diferença entre os valores de ψ. 90

Função de corrente • O sinal de ψ é tal que de frente para a direção do movimento, ψ cresce para a esquerda. • Isto também pode ser visto a partir da definição, Eq. (35), para a qual a derivada de ψ em uma direção fornece a componente da velocidade em uma direção tal que forme um ângulo de 90° (em sentido horário) em relação à direção de diferenciação. • Uma finalidade de se definir uma função de corrente é relacionada à plotagem de linhas de corrente. 91

Função de corrente • Outra razão está relacionada à diminuição do número de equações simultâneas a serem resolvidas. Por exemplo, para um escoamento viscoso próximo a uma fronteira sólida plana, tem-se que as equações de conservação da quantidade de movimento e de conservação da massa são dadas por (38) (39) 92

Função de corrente • Um par de equações simultâneas em u e v pode ser combinado em uma equação simples definindo-se a função de corrente: • Tem-se então uma única função desconhecida e uma única equação diferencial. A equação da conservação da massa é satisfeita automaticamente. 93

Coordenadas polares • Em certos casos, é mais conveniente em se trabalhar com coordenadas polares, especialmente em problemas envolvendo fronteiras circulares. De fato, frequentemente seleciona-se um sistema de coordenadas que se adapte à geometria do corpo (fronteira). • A seguir será apresentado o procedimento de transformação da Equação de Laplace 94

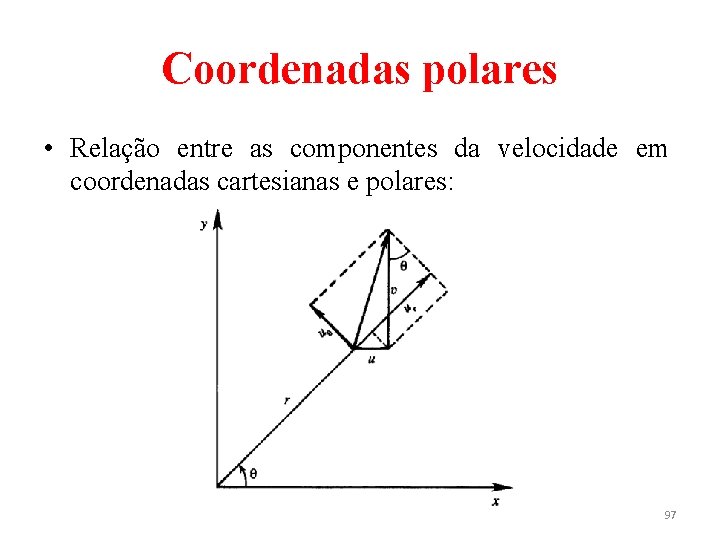
Coordenadas polares • Os sistemas de coordenadas cartesianas e polares estão relacionadas pelas expressões (40) • Primeiramente, serão determinadas as componentes polares da velocidade em termos da função de corrente. 95

Coordenadas polares • Uma vez que ψ = f(x, y) e que x e y são funções de r e θ, através da regra da cadeia obtém-se • Omitindo-se os parênteses e subscritos, tem-se (41) 96

Coordenadas polares • Relação entre as componentes da velocidade em coordenadas cartesianas e polares: 97

Coordenadas polares • Observa-se que • de modo que • Observa-se também que 98

Coordenadas polares • As componentes polares do vetor velocidade estão relacionadas à função de corrente por • Tal resultado está em conformidade com a observação prévia de que a derivada de ψ fornece o componente da velocidade em uma direção 90° no sentido horário da direção de diferenciação. 99

Coordenadas polares • Para se escrever a Equação de Laplace em coordenadas polares, tem-se da regra da cadeia • Diferenciando a expressão anterior em relação a x, tem-se (42) 100

Coordenadas polares • De modo análogo, tem-se (43) • Somando-se as Eqs. (41) e (42), obtém-se • completando a transformação. 101